属性动态更新的一种三支决策模型
2020-12-11孙小军
徐 怡,孙小军
(安徽大学 计算机智能与信号处理教育部重点实验室,合肥 230601)
(安徽大学 计算机科学与技术学院,合肥 230601)
1 引 言
三支决策理论最初由Yao教授提出的[3],是近些年来出现的新的决策分析理论,可以用于处理不完整、不精确信息.三支决策模型作为传统二支决策模型的重要扩展,考虑了决策过程中的诸多不确定性因素,在处理过程中,当信息不足以决定接受或拒绝时,将延迟决策作为的第三种决策行为.目前,三支决策理论已被广泛应用于人脸识别[4]、医疗诊断[18]、推荐系统[5]等多个领域中.
粗糙集和决策粗糙集理论[1]是三支决策研究的起源,三支决策的正域、边界域和负域可以通过通过粗糙集的上下近似集给出一定的语义解释.在粗糙集理论模型中,Yao引入了 Bayes风险决策方法,依据最低风险代价,把对象划分到正域、负域和边界区域,从而形成了三支决策的接受决策、拒绝决策和延迟决策的三支决策语义[2].近年来,许多学者研究了将朴素决策理论转化为理论体系、信息处理模型或计算方法的问题,已取得显著进展的三支决策模型及其应,例如三支聚类分析[6,7],过滤垃圾邮件[8],三支决策空间[12],代价敏感三支决策[9,11],三支决策概念分析[13,14]等.许多关于三支决策理论的研究都是基于相应的决策背景及其应用.例如,Li和Zhou[15]结合决策者不同的风险偏好,提出了一种基于决策理论粗糙集的新决策模型.Yang和Yao[16]提出了一种多级代理三支决策模型,描述了当不同的用户根据自己的标准给出不同的决策集时,如何制定一个全面一致的决策标准.Yang和Li[20]提出一种基于三支粒计算的混合数据融合的方法.Luo[17]提出一种基于多源信息系统构建三支决策的方法以及在系统中的应用.
然而,对于接受区域内的对象数量固定且实时划分对象的情况,在目前研究领域中很少有人提出相关的三支决策的模型和理论.当论域U是排序的属性值时,Zhang[10]等提出了一种基于标准差构建最佳偏差以及动态的更新属性值的三支决策模型,但Zhang没有考虑属性值更新前后的关联性以及重要程度.本文考虑属性值更新过程中的联系以及重要程度,提出一种基于基尼系数来构建离散度偏差,动态更新属性,动态的计算一对阈值来构建三支决策,是一种基于属性更新的动态决策模型.
在一些在线实时评判系统中,需要实时的筛选出一批对象,评判的数据不是一次性都到达,而是随着时间逐渐获取,且需要在每个时刻都要选出一批对象,现已如下场景为例:
假设需要实时考核,选拔k个优秀学生,通过成绩从高到低排序,每次考核选出部分学生和淘汰部分学生.运用三支决策分类算法,每次将一批学生分类到三个不相交的区域:POS、BND和NEG,其中POS区域中是选中的学生,NEG区域中是淘汰的学生,而BND区域中是不能确定结果的学生,需要继续考核.通过t次考核,从N个学生中选择k个 “最优” 的学生作为最佳的分类(N>k).
对于这种实时多次的考核,如果运用二支决策思想,直接在某次考核中把前k个最高成绩的同学当作最佳分类,如果有的学生本次考核不良,即使下次考核表现优异,但也错失分类成优秀学生的机会.显然这种二支决策的方法过于直接和武断.容错性较差,缺乏处理不确信性的能力.
而本文所提出的基于基尼系数构建离散度的三支决策模型能很好的解决该问题,克服二支决策的问题,提高容错性和处理不确定性的能力,能够处理实时数据的划分问题,同时解决属性值更新过程中的关联性和重要程度问题.本文第一节简要介绍了粗糙集和三支决策理论;第二节介绍了基于基尼系数构建离散度的三支决策模型及相关定义.第三节通过对比基于标准差的三支决策算法(FEAOAV)[15]的实验验证了算法的可行性和有效性.最后总结全文.
2 粗糙集与三支决策理论
定义1.序信息系统S=(U,AT,V,f)被定义为一个四元组,其中,论域U为非空有限的对象集合;AT为非空有限的属性集合,∀a∈AT;V是全体属性的值域集合,即V=VAT=∪a∈ATVa;f表示信息函数,∀x∈U,定义f(x,a)表示x在属性a上的取值,则有f(x,a)∈Va,且满足序关系(f(x,a),≥).
定义2[1].序信息系统S=(U,AT,V,f),∀a∈AT,∀X⊆U,概念X的下、上近似集合分别定义为:
其中[x]a表示x在a上的等价类.
定义 3[10].根据子集X的下、上近似集合,可将论域划分为3个互不相交的区域:正域POS(X)、边界域BND(X)和负域NEG(X),将其分别定义如下:
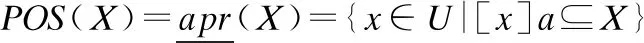
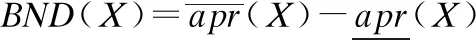
由正域中元素导出的规则表示确定属于X的规则,由负域中元素导出的规则表示确定不属于X的规则,而由边界域导出的规则表示可能属于X的规则,这体现了“三支决策” 的基本思想.
3 基于基尼系数的动态三支决策模型
对于后续出现的对象集,如无特别说明,则默认为:对象集U={x1,x2,…,xn}表示本次要划分的重新降序排列后的对象集合,不包括“上次”已经划分到正域POS和负域NEG中的对象.对象的属性值都为数值型.
3.1 属性的动态更新
文献[10]叙述属性动态更新的三支决策划分过程,现简要介绍:
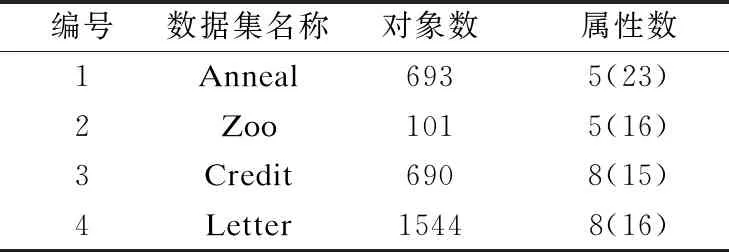
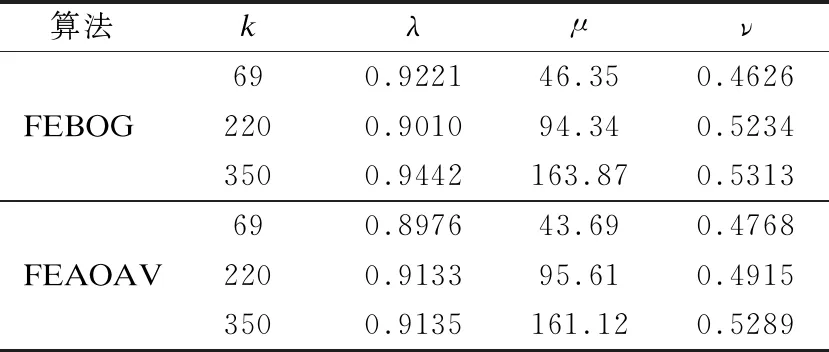
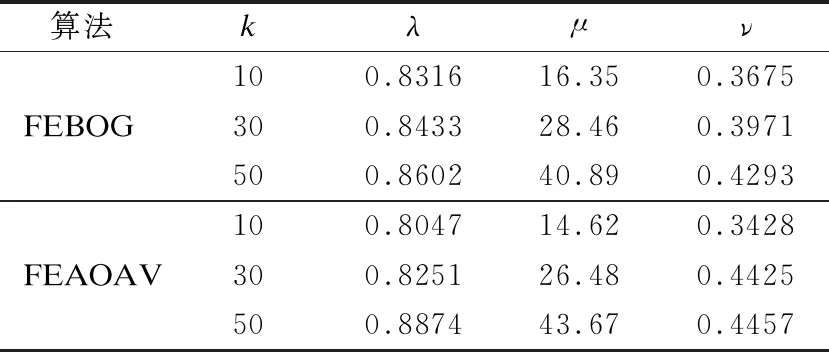
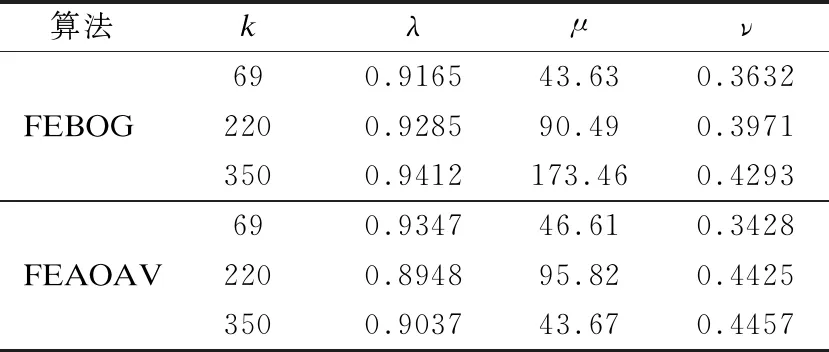
有对象集U={x1,x2,…,xn},Zi={z1,z2,…,zm}为U中对象xi的m个属性值的集合,现需要选出k个“优秀”的对象.在第j次决策(j ·将确定为“优秀”的对象直接划分到POS接受区域中,然后完成所有属性值的更新. ·那些可能是“优秀”的对象被放入BND延迟区域,然后再次更新它们的属性值,之后再对它们进行划分. ·不是“优秀”的对象直接放入NEG拒绝区域.重复上述过程,直至POS接受区域的对象的数量等于k. 在实际操作中,如果最终更新后的对象的数量没有达到k,直接从前面BND延迟区域(不足,则继续从拒绝区域NEG)选择一部分拥有更高的属性值的对象纳入到对象的POS接受区域,使POS接受区域数量等于k. 在上面的决策过程,更新的属性值的重要程度不同且有一定的关联性,在“理想”的决策过程中,一个对象是否是“优秀”的对象,不能直观地知道.在一个连续的决策过程中,决策是一个价值更新的动态过程.当固定接受区域内的对象个数和对象的属性逐个获取,本文将给出基于基尼系数的三支决策模型,利用基尼系数动态计算阈值,动态的划分出“优秀”的对象. 定义 4.序信息系统S=(U,AT,V,f),设U={x1,x2,…,xn}是第t次更新后对象集,V={v1,v2,…,vn}是U中对象的第t个属性的值域的集合,则xi在第t次更新后(第t个属性)的值域定义如下: (1) 给予对象xi在每次更新后的值一个权重b,能够体现每次更新的重要程度,同时定义4将每次更新的值关联起来. 定义 5.(属性比)序信息系统S=(U,AT,V,f),令U={x1,x2,…,xn}是对象集,其中a∈AT,a(xi)表示m在属性a下的值,对于一个属性a的值为数值型,对象xi的属性比定义如下: (2) 从属性比的定义可以得出以下两个结论: ·如果两个对象属于一个等价类,则它们具有相同属性比.(如果两个对象xi和xj的属性a的值相等,则认为在a属性下xi和xj属于同一个等价类,即[xi]a=[xj]a. ·对象同一属性下值域越高,对应的属性比越高. 定义 6.(基于属性比的三支决策模型)序信息系统S=(U,AT,V,f).对于X⊆U,带有一对阈值(α,β),(0≤β≤α≤1) 的上下近似集定义分别为: (3) (4) U可以分为三个互不相交的区域,即接受区域、延迟区域和拒绝区域,如下所示. (5) (6) (7) 接受区域内的所有对象都是“优秀”对象,拒绝区域内的所有对象都是“淘汰”对象,在当前条件下,延迟区域内的对象都不容易清晰判断,需要进一步观察. 在定义6中,当α和β的阈值确定,所有的对象可以划分到接受区域,延迟区域,或拒绝区域.在动态决策的整个过程中,对象的属性值和接受区域内所需的对象数量都可能发生变化.因此,相应的自适应阈值α和β需要改变.因此,本文研究的下一个目标是在给定可接受区域内的对象数量和属性值时,寻找一对自适应阈值. 为了确定阈值α和β,必须选择一个适当的特征提取方法.因此,本节根据离散集的数学特征提出一种新的偏差概念定义如下 定义 7[19].(基于基尼系数的偏差)定义U={x1,x2,…,xn}是对象集,Vn={v1,v2,…,vn}是U中对象在属性a下值域的集合,U满足序关系f(xi,a)≥f(xi-1,a),即vi≥vi-1,则, dn=Gn-Gn-1是对象xn的偏差. (8) Vn-1比Vn少一个元素vn,当Vn-1中加入一个元素vn时,即Vn-1变成Vn时,Vn-1的离散度可能会变化,这种变化的程度可以归结为增加了一个元素在其中,偏差的概念反应这一动作的影响程度. ·当dn>0时,我们说元素vn的加入对集合Vn-1有一个负的影响; ·当dn<0时,我们说元素vn的加入对集合Vn-1具有正影响; ·当dn=0时,我们说元素vn的加入对集合Vn-1没有影响. 例1.假设有两个集合V3和V4,按值降序排序,其中V3={2,3,5}和V4={2,3,5,10},计算d4. 第1步.计算两个集合的和: 第2步.计算G3: 第3步.计算G4: 第4步.计算出d4=G4-G3=0.125. 在上述数学分析的基础上,提出一种基于基尼系数的对象属性值偏差的算法(FEBOG),用于实际的优化选择过程.该算法的基本目的在一次决策中,得到一组对象的偏差值. 算法 1.计算一组更新后属性值集合的偏差值. 输入:更新后属性值域的降序集合Vn={v1,v2,…,vn}; 输出:偏差值集合D={d1,d2,d3,…,dn}. Step 1.利用Sn集合构造序列集合 V1={v1};V2={v1,v2};V3={v1,v2,v3}…Vn={v1,v2,v3,…,vn}. Step 2.计算每个集合的基尼系数. G0=0;G1=0; … Step 3.计算对象偏差序列 d1=G1-G0;d2=G2-G1; Step 4.得到离散度偏差集Dn={d1,d2,d3,…,dn}. 上述算法步骤表明,对象的特征(对象的偏差值)基于集合的基尼系数计算.对象的偏差值可以反映对象加入集合后对集合离散度的影响.因此,决策模型中对象的偏差值的意义可以重新解释如下: 让Xj-1={x1,x2,x3,…,xj-1}表示“优秀”对象集.另一个对象集Xj={x1,x2,x3,…,xj-1,xj},通过FEBOG算法算得对象的属性值特性dj. ·dj>0代表的元素xj有一个负面影响,这降低了Xj-1整体的优秀程度; ·dj<0代表的元素xj有一个积极的效果,提高了Xj-1整体的优秀程度; ·dj=0代表的元素xj没有效果,对Xj-1整体的优秀程度没影响. 对于属性值动态更新,文献[10]提出一条规则:对象的属性值越低(高),其增量就越大(低).并且进一步阐述了:如果xi和xj是两个在a属性下具有最大偏差的对象,则xi和xj可以作为论域U的两个分类点,最合适的决策阈值α和β能够被xi和xj的属性比获得,论域U可以被分为三个不想交的区域POS,BND,NEG. 一次决策过程是,根据属性值由高到低的顺序,依次将对象添加到“优”对象集中.当一个属性值较低的对象被添加到一个“优”对象集中时,“优”对象集的离散度降低.显然,通过FEBOG算法可以得到集合离散度的变化,即每个对象的偏差值表示其在这个过程中的影响程度.如果一个对象的影响程度高于添加到“优秀”对象集中的任何其他对象的影响程度,这意味着在添加此对象之前,“优秀”对象集已经是稳定且集中的.因此,根据每个对象的最优偏差,可以将域分为三个相对稳定且集中的对象集,分别为接受区域、延迟区域和拒绝区域. 图1 一次三支决策形成的区域Fig.1 Region formed by one time three-way decision 因此,在一次决策过程中,自适应分类方法可以描述为:域的三个区域如图1所示,其中k表示给定的被接受区域内的对象数量,U={x1,x2,x3,…,xn}表示根据属性值由高到低设置的对象集.应用FEAOAV可获得各目标的最优偏差. 首先,k是U的一个分类点;U分为两个不相交子集X1={x1,x2,…,xk}和X2={xk+1,xk+2,…,xn}.然后,假设1≤i≤k和k+1 POS(α,β)(X)={x1,x2,…,xi-1} (9) 因此,阈值α,β能够通过以上分析得出: (10) (11) 该算法会出现以下几种情况: 1)前m次(m 假设要在t次分类中选出k个对象,令在前0.5t次分类中,如果划分到POS正域中的个数m大于0.5k个,则每次只选出前a′个对象到POS正域,其中a′=0.5m,(0.5m 图2 划分次数过少的解决办法Fig.2 Solutions for too small division times 如图2所示,在第M次的分类点为xa和xb,但a>k,通过调整后分类点为xa′和xb,a′ 2)在规定的t次分类中选出来的对象个数m小于k,此时可以在BND边界域中选择前k-m个具有最大值的对象作为需要的对象,如果边界域对象个数不足,则继续从负域中选择相应的具有最大值的对象作为需要的对象. 图3 接受区域对象个数不足的解决办法Fig.3 Solution to the insufficient number of objects in the receiving area 如图3所示,在第t次分类后的分类点为xa和xb,但a 算法 2.接受区域划分k个对象的三支决策算法. 输入:信息系统S=(U,AT,V,f),需要选出的对象个数k,预计划分次数t; 输出:集合POSt的k个对象. 1)初始化,POSt=∅,U={x1,x2,…,xn},已选出的对象个数m=0,已划分次数h=1,权重b=t-1; 2)对于(|POSt| (2)根据算法1计算出Dn={d1,d2,…,dn},找出两个最大的值di和dj,对应的对象为xi,xj; (4)根据定义6计算出: POS(X)={x1,x2,…,xi-1}; (5)If |POS(X)|>0.5 &&h<0.5: POS(X)取前0.5|POS(X)|个对象; POSt=POSt∪POS(X); (6)h=h+1,U=BND(X); 3)If(|POSt| 4)输出:POSt集合. 文献[10]中对具有属性动态更新的三支决策模型给出了评估方法,分别衡量模型的精度性能,最优率,与“最优”分类结果的相似度. 代表三支决策分类结果与“最优”分类结果的相似度,越大越好,其中POS*(X)代表最优分类的对象集,是所有更新操作完成后,前k个最大属性值的对象组成的集合. 代表三支决策分类的对象的属性值总和与二支决策分类的对象的属性值总和之差,衡量提出的模型的精度性能,其中POS(X)O表示二支决策模型接受区域的对象集. 代表最优率,也就是说,根据搜索“最优”分类结果过程中需要更新的对象数量,在三支决策过程中减少了更新的对象数量,其中,|NEGi(X)|代表第i层决策分到拒绝区域的对象个数,N代表决策对象的总数. 为了验证本文算法的有效性,将其与文献[10]中的FEAOAV算法进行比较.算法的仿真实验环境为:Windows7操作系统,配置为Intel(R)Core(TM)i3-4170CPU@3.70GHz,内存为8GB,使用java语言实现算法.算法测试使用的4个数据集均来自UCI数据库.在进行实验之前,首先对数据进行处理,需要的数据的属性是数值类型且值域范围较大,所以选取数据集的部分数值类型属性并改造属性值,使得新属性值为原属性值加上0-g之间的随机数(g为数据集的对象数),改造后的数据集1的属性数由23变为5,数据集2的属性数由16变为5,数据集3的属性数由15变为8,数据集4的属性数由16变为8.如表1所示. 表1 实验中使用的UCI数据集Table 1 UCI dataset used in the experiment 表2-表5为本文算法(FEBOG)和FEAOAV算法在不同数据集上的对比实验结果,t为划分次数,即为改造后的属性数,N为总的对象数量,k为正域POS需要的对象个数,λ,μ,ν 表2 Anneal 数据集Table 2 Anneal dataset 表3 Zoo 数据集Table 3 Zoo dataset 表4 Credit 数据集Table 4 Credit dataset 表5 Letter 数据集Table 5 Letter dataset 为3个评估指标.其中,表2设置t=5,N=693,表3设置t=5,N=101,表4设置t=8,N=690,表5设置t=8,N=1544.为了确保数据的客观性,实验结果为运行50次后取的平均值.从表2-表5中可以看出所有数据集上,在不同的k值上,本文算法大部分的λ,μ,ν指标值大于FEAOAV算法,且随着k的增大,λ,μ,ν值的增幅大于FEAOAV算法,说明本文算法在划分性能优于FEAOAV算法.λ能达到0.9714,说明本文模型有较高的可行性.ν的值在0.3632-0.3632之间,说明对比“最优”分类结果,本文算法能够减少0.3632-0.3632的对象的更新,表明具有较高的效率.所有的μ都大于0,表明在许多的动态决策问题上本文算法优于二支决策模型. 在接受区域的对象个数固定的这种情形时,人们通常采用二支决策的方法来解决问题的最优解.但是,由于更新过程中忽略了不确定性和成本,结果往往不合理,同时相应的三支决策模型没有考虑属性更新前后的关联性和重要程度,且很多情况下需要实时多次的划分,评判的数据随着时间逐渐到来.为了解决这些问题,首先,提出属性动态更新规则,建立更新前后的属性的联系和重要程度,然后根据对象的价值特征(偏差)和二支决策模型的不足,建立了一个动态的三支决策模型.然后,在给定目标属性值排序的条件下,提出了一种基于基尼系数的属性值特征提取算法FEBOG.并在此基础上,提出了一种自适应划分方法,并确定了一对阈值的计算方法,做到动态实时划分.针对两种分类异常情况,提出了解决方法.该模型可以在动态决策过程的最后获得二支分类结果.最后进行了仿真实验,实验结果表明,基于FEBOG算法的三支决策模型在λ,μ,ν指标上部分优于基于FEAOAV算法的模型.本文模型适用于非监督学习,可以应用在一些选拔比赛中,每轮比赛选出和淘汰一批选手,直到若干轮后选出合适数量的选手.本文模型还可以应用在一些在线学习中,及时动态的处理到来的数据.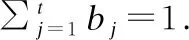
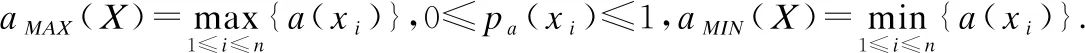
3.2 自适应阈值的计算

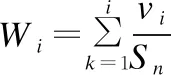
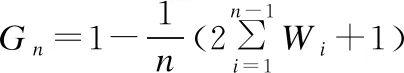
d3=G3-G2;…dn=Gn-Gn-1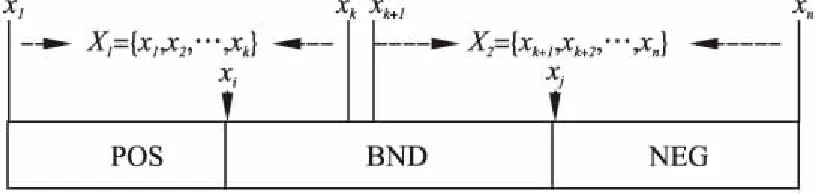
BND(α,β)(X)={xi,xi+1,…,xj-1}
NEG(α,β)(X)={xj,xj+1,…,xn}3.3 划分异常情况的解决
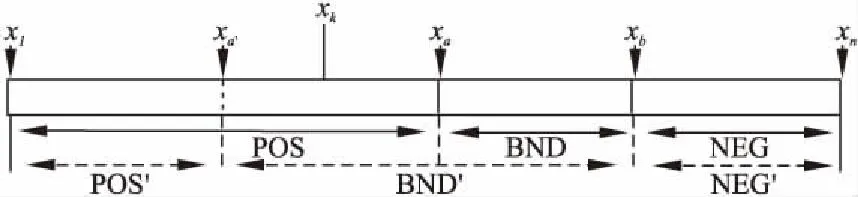
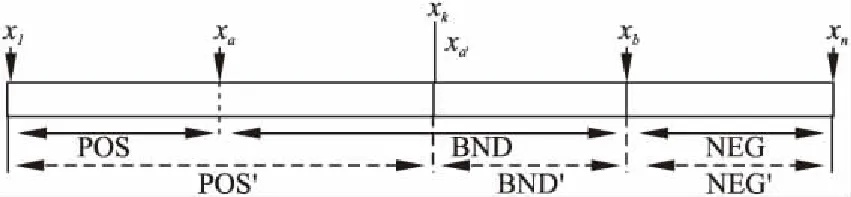
BND(X)={xi,xi+1,…,xj-1};
NEG(X)={xj,xj+1,…,xn}.
Else:POSt=POSt∪POS(X);4 仿真实验
4.1 模型的评估
4.2 实验分析

5 结 论
