如何在应用问题中培养学生的画图能力
2020-12-10庄辉龙
庄辉龙

摘 要:数学应用问题情境复杂、抽象难懂,对于低学段的儿童来说具有较大的难度,如何让抽象应用问题具体化和形象化,是每个数学教师需要探究的问题,而作图在解决问题中具有不可比拟的优势。文章结合多个教学案例呈现课堂实践:以“简单符号”为载体,表达数量关系;以“简单的示意图”为依托,表达数量关系;以“直观图”为延伸,分析数量关系。在这个过程中,帮助学生高效率地解决应用问题,同时提升学生的画图能力。
关键词:小学数学;简单符号;示意图;直观图;画图能力
随着新课程改革的深化,解决问题已经成为小学数学教学中举足轻重的一部分,在考试中占据着较大的分值,其重要地位不言而喻。而解决问题离不开作图,作图是帮助学生进行思考的重要方式。同时作图法是渗透数形结合思想的重要载体,同时也可以培养学生的几何直观这一重要数学核心素养。基于小学生的年龄特征和认知结构,不难看出作图在解决问题中具有不可比拟的优势,一方面,直观的图形可以引发学生的联想,化抽象为直观,帮助学生快速简捷地解决数学问题;另一方面,它与小学生学习过程的需求相切合,可以促使学生建构良好的认知表征。作图能力如此重要,教师该如何在低学段教学中逐步渗透和培养呢?笔者结合教学实践,从以下方面进行阐释。
一、以“简单符号”为载体,表达数量关系
低年级数学教材中数学解决问题大多数以直观情境图为主要呈现方式,而学生在理解抽象的数量关系上存在着或多或少的问题,这时通过简单符号则可以帮助学生理清其中的数量关系,找寻到解决问题的策略,成功获取结论。
案例1 以“直观情境图的解决问题”的教学片段为例
师:大家请看以上的图1和图2,我们是否可以通过简单的符号来表示其中的信息?
生:可以。
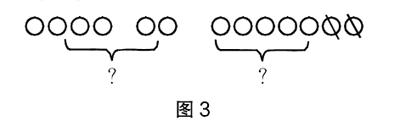
师:那我们一起来试一试吧。(学生纷纷进入画图状态,并呈现了如图3所示的图形)
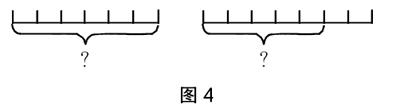
师:大家都画得非常棒,通过简单的示意图,可以让其中的数量关系显性化,对应用问题的解决有着重要的意义。事实上,我们还可以简化为以下线段图。(出示图4)
教材中图文结合所呈现的是生活情境中的应用问题,题中不仅呈现了信息,也蕴含了需要解决的问题,需要学生去找寻其中的信息并独立解决问题,此时简单的学具和符号在解决这一类问题中起到了“搭桥”的作用,形成了解决问题的策略,让学生轻松愉快地解决复杂关系的应用题,在培养学生能力的同时,提升了学生的学习兴趣,从而大大提升了教学效果。
二、以“简单的示意图”为依托,表达数量关系
数学问题中的比多少、几个几和平均分问题都源于不同的数量关系,对于低学段的学生来说难度较大,较易产生误解,如果能以简单的示意图为依托作为一个观察点,就可以让学生直观地理解和分析题意,让学生利用已知经验去建构,并为后期学会作线段图打下坚实的基础。
案例2 例题:试比较以下两道题,并选择合适的方法解答。
(1)教室里有4排课桌,每排有5张,一共有课桌多少张?
(2)舞蹈教室有2排桌子,一排有5张,另一排有4张,一共有桌子多少张?
在解答本题中,教师可以引导学生观察如图5所示的示意图,让学生通过简洁的语言来阐释图示中的数量关系,并通过思考将图示转化为正确的算式,让学生通过动手、动口、动脑等多感官参与,获取更多的画图体验,充分发挥图示的转化作用,体验画图的意义。
问题:如图6,小红来到小商店购物,她想要买3个皮球,需要付多少钱?
本题多余条件较多,情境相对较为复杂,需要学生通过乘法的意义来分析和理解,理清其中单价、数量和总价的数量关系。在教学过程中,教师可以引导学生从购物经验和对乘法意义的理解层面,借助简单的示意图来分析其中的数量关系,并以“几个几”的形式去表征,从而建构起对数量关系的深刻认识。学生经过思考可以快速画出如图7所示的示意图,深化对“倍”的认识,进一步形成正确的解题路径。
为了营造画图的外部环境,我们需立足于应用问题的逻辑结构,让学生感受到画图形象化和具体化的特征,看清简单示意图对数学理解的意义,对理清数量关系的作用,对正确解题的促进效果,从而自然运用到日常的解题中去。
三、以“直观图”为延伸,分析数量关系
不少教师一直都在探索用图示更清晰表达数量关系的形式,图示法本身就是数形结合的训练,如何让学生自然运用图示是大部分教师所要探究的问题。如果在课堂教学中能经常这样引导学生进行直观图的训练,学生的画图能力何愁不会提高。事实上,不仅“数与代数”领域的问题解决可以图示的方式来诠释其中的数量关系,图形和几何、统计与概率也可以通过直观图来表达其中的数量关系 [1]。
案例3 课题:测量旗杆的高度
师:大家回忆一下我们学习的旗杆,有谁知道它的高度是多少呢?(学生猜测)
师:这个问题的难度比较大,如图8,大家知道一根旗杆的高度是13厘米,还是13米呢?(学生叽叽喳喳地比画着)
生1:当然是13米,13厘米就这么一点长。(生1比画)
师:很好。13厘米就相当于一拃长,生1是通过排除法来解决这个问题的。事实上这个问题的解决方法有多种,如推算法和类比法,我们来了解一下推算法,以你的身高作为参照物进行估测,旗杆的高度相当于几个小朋友的身高呢?大家是否可以试着画一画估测的直观图呢?(学生进入画图状态,很快生成了图9所示的直观图)
师:非常好,从刚才的分析中我们发现确定物体长度的方法有很多种,我们在选择合适的长度单位时不仅需要多思多想,还可以通过直观图的方式,一目了然地找寻问题的答案,最终确定合适的长度单位。下面我们就通过这样的方法来完成以下的练习。
以上案例中,教師通过精心设计典型性的问题情境,让学生的思维经历一个层层递进的思维过程,通过图示将学生无法用语言表达的分析过程进行阐释,使学生的头脑中逐步形成关于长度单位的认知体系,并在此基础上通过画图深化学生对数量关系的理解。
综上所述,图示使应用问题中的隐形条件显性化,让复杂的数学问题简单化,在应用问题的解决中培养学生的画图能力是行之有效的 [2]。当然,学生画图能力的提升并非一蹴而就的,需要教师在长期的教学过程中不断渗透和加以培养,增强学习的趣味性,调动学生学习的自主性,从而发挥学生的学习技能,让学生的画图能力和数学素养落地生根。
参考文献:
[1] 赵生初,许正川,卢秀敏. 图形变换与中国初中几何课程的自然融合[J]. 数学教育学报,2012,21(4).
[2] 殷晓波. 小学数学教学中学生画图能力的培养探寻[J]. 新课程导学,2013(24).
