浅谈如何在分数学习中培养小学生“数形结合”思维方式

胡俊

摘 要：“数形结合”是数学学习中非常重要的一种思维方式，是至关重要的教学手段。掌握好“数形结合”的方法与思想，能够很好地帮助学生构建数学模型。小学阶段分数方面的知识内容较为抽象，学生利用“数形结合”思维方式，能够有效地理解分数之间的关系，并突破学习中诸多难点。文章将就如何在分数教学中培养小学生的“数形结合”思维方式进行分析，以期为小学数学教学提供理论参考。

关键词：分数教学;数形结合;思维方式

中图分类号：G623.5 文献标识码：A 收稿日期：2020-05-19 文章编号：1674-120X（2020）28-0049-02

一、培养小学生“数形结合”思维方式的原因

数学是以数与形为基础对象的学科，一切数学问题都是围绕数与形的演变、发展而展开的。“数形结合” 就是根据数量与图形之间的对应关系把抽象的数学语言与直观的图形相结合，使抽象思维和形象思维相结合，是一种常用的数学方法。在数学发展进程中，数与形于内容上互相联系，于方法上互相渗透，彼此间在一定的条件下互相转化。小学生的思维正处于由具体形象思维向抽象逻辑思维过渡的时期，而抽象逻辑思维仍具有很强的具体形象性。

例如，在教学分数大小比较的内容时，教师如果干巴巴地讲解二分之一大于三分之一，学生可能并不能够理解。因为在学生的认知里二小于三，可是在分数中二分之一大于三分之一。

例如，在讲解分数时，教师采用讲故事的方法：“猪八戒分西瓜。猪八戒刚咬第一口，悟空就从天而降。孙悟空说：‘我吃西瓜的二分之一。八戒心里一直想多吃点，听了高兴极了，说：‘我可要吃八分之一。。”学生这时候就议论纷纷了，到底谁吃得多呢？如果没有“数形结合”，学生就不能够准确地理解到底谁吃得多。

因此，在分数的教学中，教师可利用图形来表示具体的量，然后根据图形间彼此的关系，适当地提出合理的分析与解释，有效地突破教学中的重难点问题。学生运用“数形结合”的思维方式进行分数学习，就是非常有效的学习方法。

二、培养学生“数形结合”思维方式的作用

“分数”对小学生来讲是一个比较抽象的概念，教师在教学实践中，要淡化分数的表现形式，注重分数的实质，以学生能力的发展为本，以解决问题为中心，以引导学生发现问题、分析问题、解决问题的逻辑性来体现教学的严谨性。

（一）运用“数形结合”思维，理解分数意义

教学中“分数”与“图形”共同渗透，让学生见“分数”就想到利用“图形”来分析和理解分数的实质，见“图形”就想到背后“分数”的意义和相关运算。

例如，北师大版教材三年级数学“分一分（二）”这一课着重研究“多个物体的几分之几”的分数意义。在开课时，教师出示图1：用下边的分数表示涂色部分对吗？为什么？以此来复习“平均分”。学生形象直观地看出图形中每份的大小不同，体验什么叫作平均分，以及平均分在分数中的重要作用，从而有效地掌握这一知识要点。

（二）运用“数形结合”思维，讲解异分母分数加减法

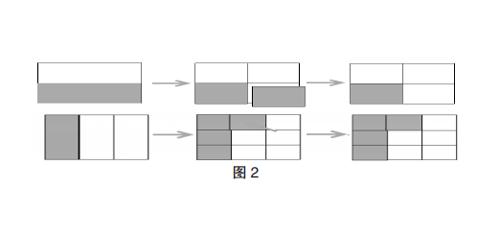
异分母分数加减法，对学生来说难点就是异分母，而“通分”这一概念有些抽象，在理解上有难度，所以有必要帮助学生构建分母相同概念，而且在理解相同单位“1”的基础上，分数才能进行加减法，这是异分母分数加减法的前提。利用“数形结合”的思想和方式，学生通过直观的图形，先把单位“1”平均分，然后进行通分，这一步骤是解决异分母分数加减法的关键和突破口。

例如：课本在设计上采用了图2的数形结合的方法，很好地体现了-，+先通分后計算的必要性，进一步借助面积模型的直观运算和通分的联系，结合方格图来说明各自思考的过程，以帮助学生在学习中，特别是在直观运算中，加深对异分母分数加减法算理的理解。

（三）运用“数形结合”思维，理解分数算理

分数乘除法教学的主要特点一是注重从不同的问题情境，引导学生多角度理解分数乘除法的意义;二是注重实践操作和各种直观模型的运用，让学生在自主探究中获得分数乘除法的计算方法。在教学过程中，教师要注重实践操作和直观比较相结合的教学方法，发展学生利用图形语言表示数量关系的思维能力，培养学生数形结合的数学思想。通过面积模型与线段图等直观数学建模，从不同角度理解分数乘除法的算理意义和计算方法，丰富学生的数学体验和学习经验。

1.分数乘法中，数形结合的合理运用

利用方格图，帮助学生理解分数与整数、分数与分数的关系，解决学习中的困难。

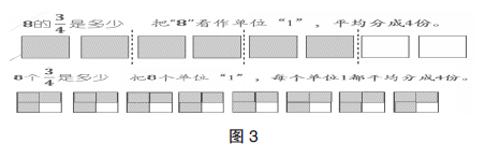
例如：8×表示什么意思？画一画，算一算。教材第25页在设计上，给出一列方格（如图3），让学生经历多种方法尝试表示8×的过程，既锻炼了学生数形结合的思想，又让学生体验表示方法的多样性，还能清楚地理解8×的算理。

2.分数除法中，数形结合帮助理解“量率对应”

在学习分数除法的意义和计算方法时，教材借助整数除法的意义，可以直观帮助学生理解除以一个非零的数，等于乘这个数的倒数。教材中设计了基于面积模型的活动，以让学生利用长方形的面积模型、线段图等直观图形，理解其中的算理和意义。特别在“量率对应‘求单位1”的处理环节中，借助直观的图形，能够有效地理清问题中的数量关系。而在教学中，教会学生这一重要技能，能够培养学生良好的数学修养，为后续学习的数学建模提供必要的技能支撑。

例如：某学校有故事书150本，故事书比科技书的本数多，科技书有多少本？（如图4）在解决这道题的过程中，首先，学生要找到单位“1”;其次，借助图形中的“故事书”与“科技书”的数量关系;再次，根据“量率对应”求出单位“1”对应的量。在解题过程中，学生可以通过数量关系直接求解，也可以根据图形的直观比较，利用方程解决问题。

小学数学中，有相当一部分的内容是计算问题。算理是抽象的、难理解的，如何把它简单地呈现出来，数形结合很重要。教师应以清晰的理论指导学生理解算理、掌握计算方法，正所谓“知其然，知其所以然”。

在分数除法这节课中，怎样让学生理解一个分数除以一个整数就等于这个分数乘以这个整数的倒数呢？比如，把一张纸的平均分成2份，每一份是这张长方形纸的几分之几呢？首先，让学生将一张纸平均分为5份，然后涂上4份的颜色，用来表示。展示图为：

然后，将这幅图的平均分为2份，再涂上颜色，如图所示：

每一份的的，使用计算公式表示为：×=

=。学生明白事实上就是乘以2的倒数。在教学第二道题目的时候：将一张纸的平均分为3份，每一份是这一张长方形纸的几分之几呢？学生很快明白了计算的道理，每一份就是的，也就是×=。这样结合图形开展教学活动，然后指导学生归纳正确的计算法则，让学生亲自经历、感受数形结合的整个过程。在图象的支持下，学生能够更好地理解算理。

（四）运用“数形结合”思维，帮助学生理解数量关系

数形结合应该全面贯穿整个小学时期，解决数学教学难题。通过数形结合的方式，表现出比较具体的、直观的数学符号，有助于分析题目中的数量关系，快速找到解决问题的办法，提升学生分析问题、解决问题的能力。

比如，应用题：根据科学规定，成人身体里面的水分占到人体体重的，然而儿童身体中的水分占身体体重的，小红身体中的水分重28千克，小红的体重是多少呢？

学生理解图片中的实际意义就是：小红体重的是小红

身体中水分的重量，进而列出数量的关系式为：小红体重×=水分的重量，然后得出方程式。解：设小红体重是x千克，那么×x=28。这样的话就等于将抽象思维转变成为直观思维来解决问题。

三、结语

坚持数形结合是很有必要的，这是尊重学生客观认知规律的。发展学生直观与抽象思维相结合的能力，提高学生的直观形象学科素养，让感性和理性认知相结合，让学生从形象理解向抽象思维延伸。把“數”和“形”有机地结合在一起，这不仅是数学自身发展的需要，也是社会发展赋予教育的基本任务。

参考文献：

[1]李 燕.数形结合，让数学思维动起来——小学数学数形结合教学实践论述[J].教育观察，2019（8）：108-109.

[2]王东凤.小学数学教学中数形结合思想的应用[J].数学学习与研究·教研版，2019（7）：61.

[3]王 倩.解析培养小学生数形结合意识的途径[J].数学学习与研究，2017（20）：46.