基于多风电相关性场景生成法的配电网随机多目标无功优化
2020-12-09崔承刚郑庆荣郝慧玲奚培锋
倪 爽,崔承刚,郑庆荣,郝慧玲,杨 宁,奚培锋
(1.上海电力大学,上海 200090;2.国网上海市电力公司,上海 200122;3.上海市智能电网需求响应重点实验室,上海 200063)
0 引言
随着高比例风电接入配电网,其出力间歇性和随机性,叠加多类型负荷波动性,容易造成馈线电压越限问题,对配电系统优化控制和运行态势预测分析带来极大困难[1]。为提高配电网对风电的接纳能力,利用OLTC(有载调压变压器)、分布式电源、储能装置以及并联电容器、SVG(静止无功补偿器)等各种设备进行无功优化,已成为改善风电接入带来的问题、提升电能质量的一项重要课题。文献[2-5]分析了风电接入对配电网的影响,并提出无功功率协调优化控制策略。由于风电具有波动性和不确定性,风功率无法准确预测,上述文献将风电等不确定性电源的出力视为确定值会对配电网无功优化产生较大误差[6],因此需要考虑大规模风电场接入的不确定性[7]。
目前,处理风电不确定性的方法通常有概率解析法和场景生成法。概率分析法一般建模复杂,计算量较大。而场景生成法将含有不确定因素的问题划分为多个确定的场景进行分析,从而避免了复杂的建模过程[8]。传统的场景生成法是以风功率历史数据为基础,针对某一时间断面或单一风电场的场景生成。文献[9]采用Wasserstein距离指标和K-means 聚类场景削减技术生成最优场景;文献[10]采用结合切片采样算法的马尔科夫链蒙特卡洛模拟法抽样生成风电场景;文献[11]基于单个风电场预测误差的多元高斯概率密度函数,通过逆变换抽样技术和场景削减技术生成大量场景。以上文献均未考虑不同风电场之间的相关性,但当大规模风电并网时,受气象及风能传播的影响,多个风电场之间出力必然会显现出一定的时空相关性,而传统场景生成法没有考虑多个风电场出力的时空相关性,具有一定局限性[12]。
针对多风电场的场景生成,文献[13-16]利用Copula 函数来对多维随机变量进行建模,将多风电场出力联合分布函数场景化,建立了场景概率模型。但是这种利用Copula 函数来构建具有相关性的随机变量概率模型的方法仅能够描绘2 个风电场之间出力的相关性,并且不能考虑风电场出力的波动性。文献[17]采用Cholesky 分解排序法描述随机变量之间的相关性。文献[18]采用秩相关系数描绘风电与负荷之间的相关性。以上文献中描述变量相关性的方法计算量较大,且缺乏对生成场景的定量分析。
针对以上问题,本文提出了一种基于多元随机变量协方差参数辨识的多风电相关性场景生成方法。该方法首先基于风电场功率的历史数据建立一种非参数的累计经验分布模型。其次,采用多元随机变量协方差参数辨识方法,生成风电场功率协方差矩阵,描述不同风电场之间的相关性。再通过逆变换抽样生成大量符合相关性和波动性特点的多风电场风功率场景,并利用Kmeans 聚类法进行场景削减生成最优场景。接着,以网络损耗最小、电压偏移最低为目标函数建立配电网随机多目标无功优化模型,并采用NSGA-Ⅱ算法求解该模型。最后,本文在改进的IEEE 33 节点进行仿真和分析,通过与传统的不考虑相关性的场景生成方法进行对比,在波动性贴合度、历史贴合度以及无功优化效果三个方面进行对比,验证了该方法的有效性。
1 多风电场相关性模型
1.1 多风电场风功率相关性模型
随着风电开发力度加大,一个地区的多个风电场在风速统计数据上呈现出一定的相关性,这将会降低含风电的电力系统可靠性。因此在对存在多个风电场接入的系统进行无功优化时,应当考虑不同风电场之间的相关性[19]。
多元风功率模型分为两类,即多元分布模型[20]和多元时序模型[21]。本文利用协方差矩阵的指数模型构建了风电的多元分布模型,并基于风功率的波动性模型设计了协方差参数辨识的目标函数,用来描述不同风电场功率之间的相关性。
1.2 基于协方差矩阵的多风电场相关性模型
含有相关性的多个风电场的输出功率可以视为一个多维随机变量P={Pk,k∈N}。假设多元随机向量Z=[Z1,Z2,…,Zk]T服从多元正态分布Z~N(μ,∑),K 为风电场个数,期望μ 是K 维零向量,则协方差矩阵∑如式(1)所示:
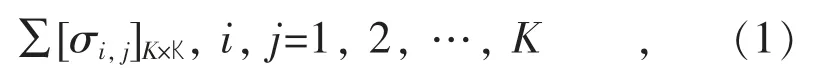
式中: σi,j为随机变量之间的协方差。
利用指数型的协方差函数对协方差进行建模:

式中: ε 为范围参数,用于表示不同风电场的随机变量Zk(k=1,2,…,K)的相关性强度。
估计最佳范围参数ε 使得随机生成的风功率场景符合风电的波动性统计规律。为此,本文引入了协方差参数辨识指标Iε[22]:

式中: S 为在数值区间[-0.15,0.15]上的等间距抽样点s 的集合;s 为抽样点;N 为抽样规模;pdf(·),(·)分别为动态场景与历史数据的风功率波动的t location-scale 分布概率密度函数值。
Iε表征了生成的风功率场景的波动与历史数据的风功率波动的差异性。Iε越小,说明生成的场景越接近历史数据的概率分布,也就越能准确描述不同风电场功率之间的相关性。
ε 确定以后,协方差矩阵Σ就被唯一确定了,那么就可以产生N 个服从正态分布的多元随机向量,再进行逆变换抽样,产生N 个多风电场的风功率场景。
2 多风电场的风功率场景生成方法
2.1 风功率的概率分布模型建立
本文采用一种非参数的经验分布函数来估计风功率的概率分布[23],即在风功率的理论分布未知的情况下,将关于风功率随机变量p 的样本x1,x2,…,xl按照单调递增排列,则风功率的ECDF(累积经验分布函数)可按照式(4)得出:
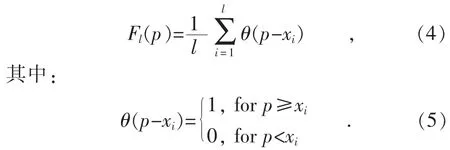
2.2 风功率的逆变换抽样
根据风功率的累积经验分布,可通过抽样法生成风功率场景。常用的抽样法有拉丁超立方抽样法、逆变换抽样法等等。其中逆变换抽样方法操作简单,适用于多个存在相关性的风电场输出功率的场景生成,因此本文选择逆变换抽样法生成场景。
假设随机变量Zk~N(0,1)服从标准正态分布,那么在已知随机变量Zk的随机数时,对随机变量Pk可以采用如下公式抽样:

逆变换抽样的示意图如图1 所示。
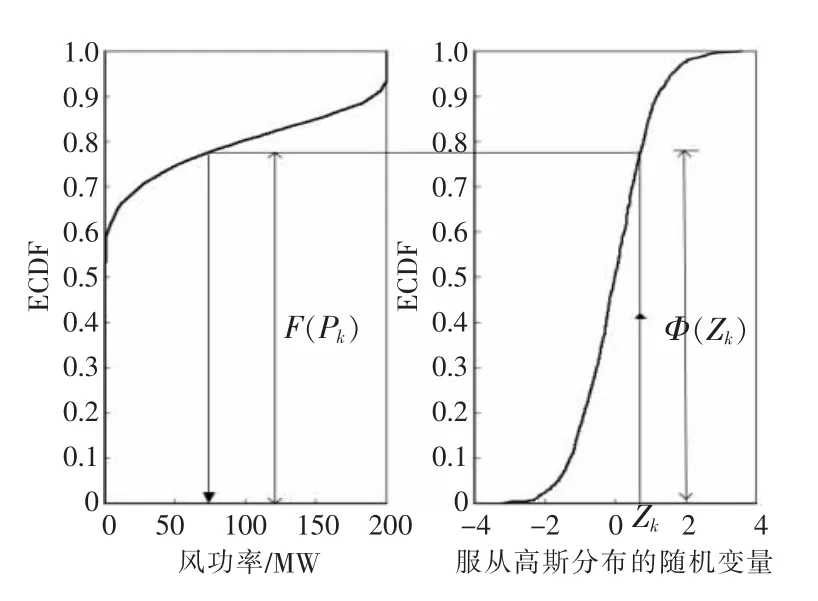
图1 逆变换抽样示意图
2.3 基于多元正态联合概率分布的多风电场场景生成
综上,基于多元正态联合概率分布的多风电场的风功率场景生成步骤如下:
(2)根据各个风电场的历史数据,计算出各个风电场的风功率波动的历史数据,并用MATLAB 工具箱中的fitdist 函数确定各个风电场的风功率波动服从的t location-scale 分布。
(3)根据式(3)确定了最佳范围参数ε 后,再根据式(2)生成对应的协方差矩阵,生成N 个服从正态分布的多元随机向量,进行逆变换抽样,产生N 个多风电场的风功率场景。
(4)采用K-means 聚类法[9]将生成的场景削减到M 个具有代表性的场景。
3 基于场景生成的配电网随机多目标无功优化模型
以网络损耗的期望最小和节点电压偏差的期望最小作为目标函数,建立含有多风电场的配电网随机多目标无功优化模型。
3.1 目标函数
(1)目标一: 网络损耗
网络损耗的期望表达式为:

式中: E()为期望;ns为场景个数;Ps为场景s 对应的场景概率;PLOSS为网络损耗;n 为系统节点数;Ui为节点i 电压幅值;Gij,Bij,δij分别为节点i 和节点j 之间的电导、电纳、电压相位差。
(2)目标二: 电压偏差
古生物学家在整理早期发现的化石时,注意到了那具于19世纪60年代在蒙大拿州出土的化石,发现其特征与肿头龙相同。这说明其实我们早在150多年前就已经发现了肿头龙的化石,肿头龙也成为了北美洲发现最早的恐龙之一。
电压偏差的期望表达式为:
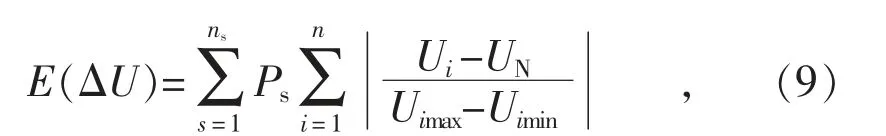
式中: n 为节点总数;Ui为第i 个节点电压;UN为系统额定电压;Uimax,Uimin为系统允许电压的上、下限,分别是1.05UN和0.95UN。
3.2 约束条件
(1)功率平衡约束

式中: Pi,Qi分别为流进节点i 的有功功率和无功功率;Ui为节点i 电压幅值大小;Gij,Bij为节点i,j 之间线路导纳参数;δij为节点i,j 之间的电压相位角(超前/滞后)之差。
(2)控制变量约束
控制变量约束主要来自变压器分接头档位T与电容器组的无功补偿容量Qc两个部分,约束关系可表示为:
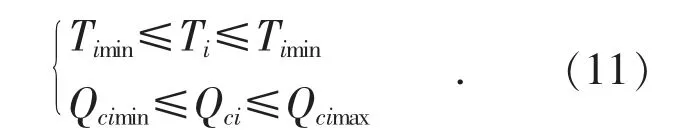
(3)电压约束

式中: Uimin,Uimax分别为节点电压幅值允许的下限和上限。
3.3 基于NSGA-Ⅱ算法的多目标优化模型求解
运用NSGA-Ⅱ算法求解配电网随机多目标无功优化问题最优解的优化流程如图2 所示。
4 算例分析
4.1 多风电相关性场景生成
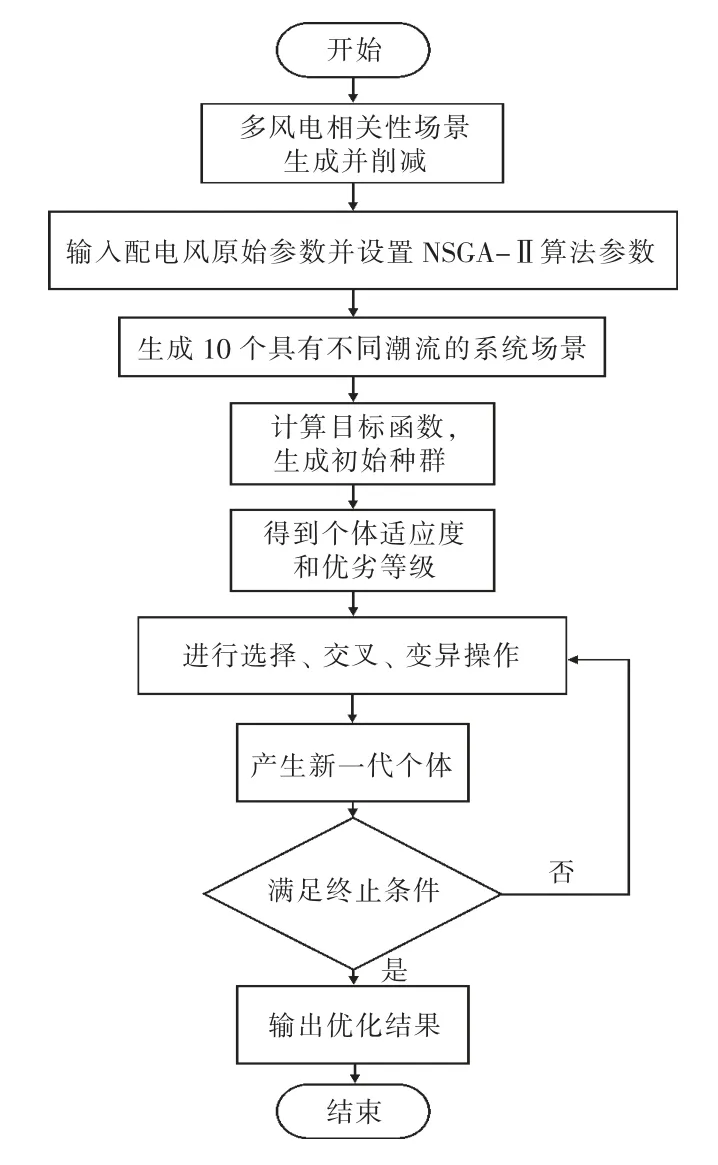
图2 基于NSGA-Ⅱ算法的无功优化流程
本文采用某地5 个风电场一年内的数据,共计15 120 组,数据采集间隔为5 min,根据本文第2 节提出的多风电场风功率场景生成方法,生成5 个风电场的累积经验分布如图3 所示。

图3 5 个风电场的累积经验分布
接着计算确定各风电场的风功率波动服从的t location-scale 分布。本文算例中5 个风电场波动性的t location-scale 分布如图4 所示,t locationscale 分布参数见附件A。
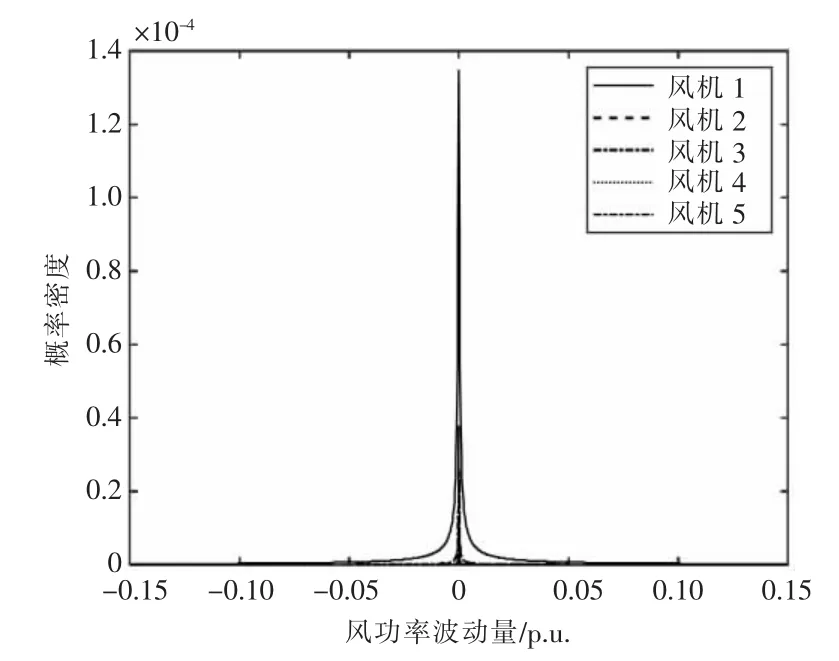
图4 风功率波动的历史数据t location-scale 分布
根据式(3),经多次寻优后最终确定本算例最佳值为83,代入式(2)后得到协方差矩阵,生成1 000 个服从正态分布的多元随机向量。接着进行逆变换抽样,产生符合5 个风电场相关性的1 000 个风功率场景。最后基于生成的这1 000 个场景,采用K-means 聚类法实现场景削减,最终得到10 个具有代表性的场景。
4.2 场景评估
为了便于比较,本文分别用传统场景生成法和多风电相关性场景生成法来生成场景。2 种方法下最终生成的10 个具有代表性的场景分布分别如图5、图6 所示。场景数据及其概率见附录B中的表B1 和表B2。

图5 传统场景生成法下的多风电场景
为了全面评价场景的优劣性,本文从风功率的波动性分布和历史数据分布两个角度来判断生成场景是否贴合实际数据。
(1)波动性贴合度指标

图6 多风电相关性场景
判断波动性贴合度,本文采用第2 章提出的协方差参数辨识的目标函数Iε,Iε表征了生成的风功率场景的波动与历史数据的风功率波动的差异性。Iε越小,说明生成的场景越接近历史数据的概率分布,也就越能准确描述不同风电场功率之间的相关性。
(2)历史数据贴合度指标
本文采用文献[24]提出的ES 指标判断场景与历史数据的贴合度。ES 指标着重于风电场景与实测值累积分布函数的距离。ES 指标如式(13)所示:
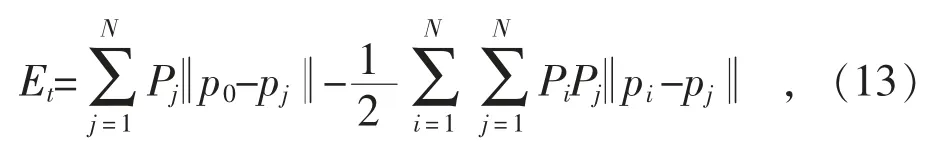
式中: N 为场景个数;Pj为场景j 的概率;pj为场景j 下的风电场出力;p0为风电场的实际出力。
ES 的值越小,则表明两者越接近,那么生成的场景更符合实际的风功率分布。
不同情况下的场景评价指标计算结果如表1所示。
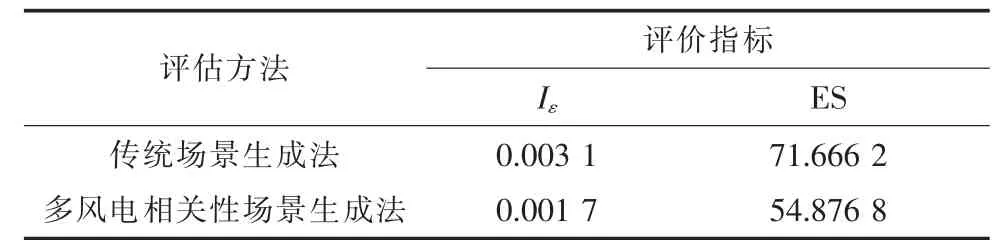
表1 场景评价指标计算结果
从表1 可以看出,在波动性和历史数据贴合度方面,考虑了采用多风电相关性场景生成方法生成的场景比传统场景生成法分别降低了45.16%和23.43%,说明考虑了相关性以后生成的场景的波动性分布更贴合实际波动,更加符合实际出力情况,更有利于不同风电场间无功优化的协调配合。
4.3 基于多风电场景生成的配电网随机多目标无功优化
本文基于IEEE 33 节点系统的拓扑结构,设计了如图7 所示的含多个风电场的配电网系统。节点1 为平衡节点;节点1 与节点2 间装设1 台OLTC,其标准变比为1,共11 个档位,变比的上、下限分别为1.05 和0.95。节点29 装设1 台SVG,其无功调节范围在[-300 kvar,300 kvar]。分别在节点15,17,22,25,32 接入风机DG1,DG2,DG3,DG4,DG5,额定功率为200 kW;电容器组每个电容大小均为212 μF。
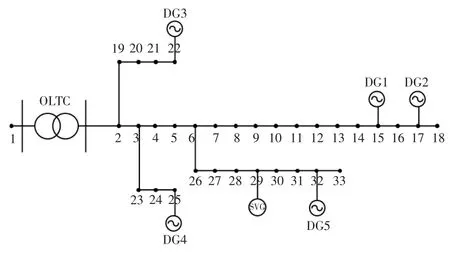
图7 改造后的IEEE 33 节点配电系统
算法参数设置如下: 群体规模设为300,Pareto 最优解集容量阈值为100,迭代次数为30,交叉概率为0.8,变异概率为0.3。
采用本文方法优化以后的OLTC 变比为1.02,SVG 补偿容量为290 kvar,电容器的最优配置方案如表2 所示。
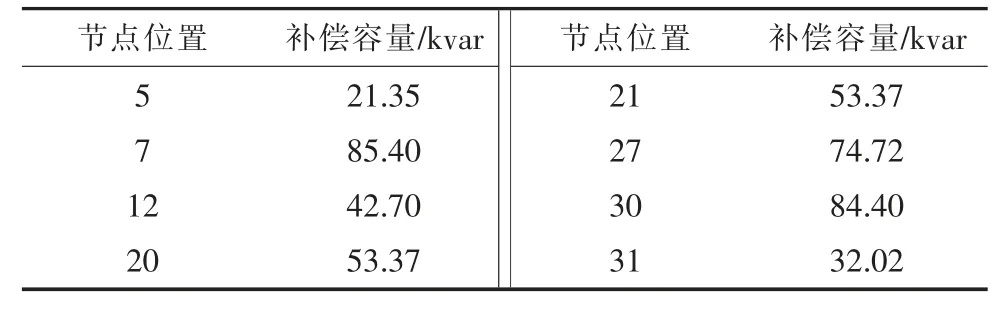
表2 电容器最优配置方案
为了便于比较,本文对基于预测值[22]、基于传统的不考虑相关性的场景生成[25]和基于多风电相关性场景生成这3 种方法的配电网无功优化策略获得最优配置方案下的优化效果进行比较。
3 种情况下生成的Parote 最优解分布如图8所示。从图中可以看出,如果不考虑场景生成,而仅用预测值进行优化,在相同的网损下,电压偏移明显大于考虑场景生成下的电压偏移值。而在相同的电压偏移下,仅用预测值进行优化得到的网损也高于考虑场景生成下的网损。说明直接采用预测值进行优化并不能很好地降低网损、提升电能质量。

图8 基于多风电场景生成的多目标无功优化Parote最优解分布
在考虑场景生成时,不考虑相关性的传统场景生成方法和基于多风电相关性场景生成方法对最优解的分布影响不大[26-32],但是考虑了不同风电场之间的相关性后,得到的最优解的范围更大,在电压偏移值较低的区域有更多解。经分析,这是因为考虑了相关性以后不同风电场之间能够相互配合出力,单个风电场的波动性降低,从而增加了电压稳定性,使电压偏移量更小,电能质量更高。因此,采用多风电相关性场景生成方法,即基于多元随机变量协方差辨识法考虑不同风电场之间相关性生成的风电场景具有更好的优化效果。
在得出最优解分布以后,本文还采用计算模糊贴近度的方法得出了接地电容的最优配置方案。表3 分别列出了基于预测值、基于传统场景生成和基于多风电相关性场景生成这3 种方法得到的最优配置方案下的网络损耗以及电压偏移。

表3 优化前后各变量对比
图9 描绘了IEEE 33 节点系统的原始电压分布以及上述3 种情况下优化后的电压分布。从图中可以看出,不同情况下配电网的最优配置方案均没有节点出现电压越界的情况。但是基于多风电相关性场景生成获得的配电网最优配置方案网络损耗更小,电压偏差值更低。这表明考虑风电场相关性场景生成的配电网优化方案电能质量更好,电能输送效率进一步提高,具有更好的优化效果。
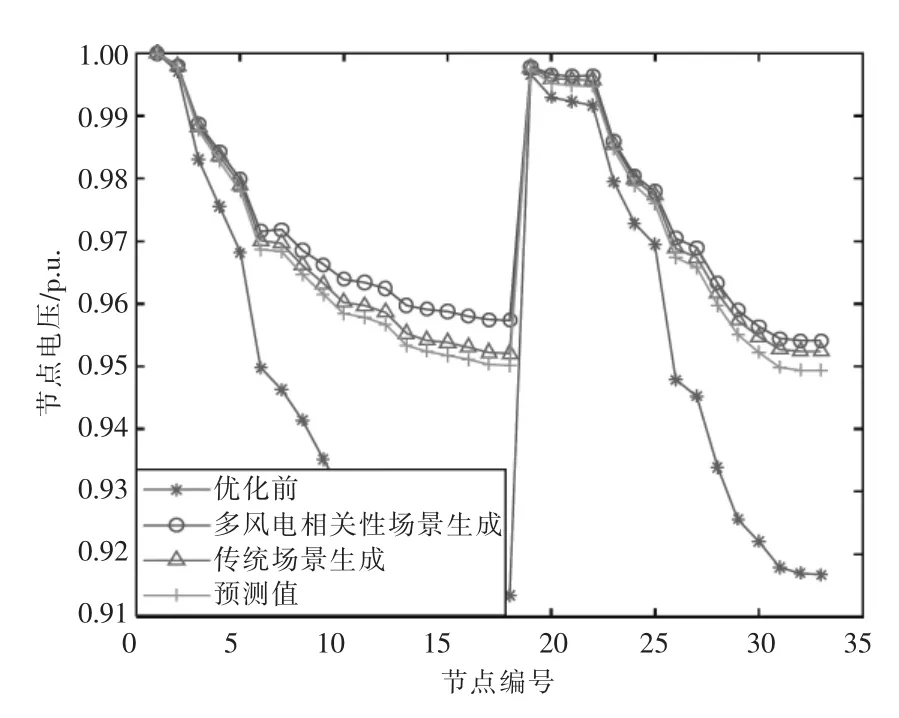
图9 不同情况下的电压分布
5 结论
本文主要研究了基于多风电相关性场景生成的配电网无功优化问题,主要结论概括如下:
(1)基于风电场的历史数据建立非参数的经验分布模型,采用多元随机变量协方差辨识方法确定最佳协方差矩阵,生成多元随机变量随机数。
(2)通过逆变换抽样得到符合相关性和波动性特征的多风电场风功率场景。利用K-means 聚类法削减得到具有代表性的多风电场景。
(3)根据生成的场景,采用NSGA-Ⅱ算法求解以网络损耗最小以及电压偏差最小为目标建立的配电网随机多目标无功优化模型,运用模糊贴近度获得电容器组最优配置方案。
(4)以IEEE 33 节点配电网无功优化问题为例,对比分析了基于预测值、基于传统场景生成方法和本文方法获得场景的波动性贴合度、历史数据贴合度以及最优配置方案优化效果。结果表明,本文提出的方法获得场景的贴合度更好,配电网无功优化效果更经济、更可靠。
附录A

表A1 各个风电场t location-scale 分布参数
附录B

表B1 传统场景生成及其概率

表B2 多风电相关性场景生成及其概率
