以加拿大为例的全球气候变化建模分析

许林峰，裴子安，刘旭程，唐聪，许弢，岳洪伟，王洪涛

（五邑大学 智能制造学部，广东 江门 529020）

全球气候变化与自然环境变化密切相关，影响着社会和经济的发展. 建立能预测全球气候变化的数学模型，对未来的环境保护和政策制定都具有重要的理论意义和现实意义. 目前，全球部分地区频繁出现“极寒天气”引发了公众对全球变暖的质疑. 在国内，李志军等[1]探讨了内蒙古气温的停滞现象. 王岱等[2]得出了中国区域极端气温（最高和最低气温）存在变暖减缓或变冷现象. 但是这些研究的数据往往受到人类大规模活动的干扰，而且上述文献以降雨量以及温室气体量等少量参数建立模型，忽略了其他因素对气候变化的关联性.

加拿大人口密度小，气候受人为影响较少，研究加拿大气候对预测全球气候变化趋势具有一定的参考价值. 因此，本文对加拿大区域气温变化及全球海洋表面温度变化趋势进行研究，利用回归分析和主成分分析等方法对气温与地球辐射、海洋温度、冰川面积、二氧化碳浓度、海平面高度、降水量和陆地温度之间的相关性进行分析，并针对极端天气提出了气候变异指标.

1 加拿大全国气温变化及海洋表面温度变化趋势

1.1 加拿大全国气温变化的时空趋势

本文研究数据来自2019年“华为杯”第十六届中国研究生数学建模竞赛. 为方便探究，首先对数据进行了分阶段处理，并进行5阶多项式拟合，其数学表达式为：

其中M是多项式的次数，横坐标x代表年份，wj是j x的系数. 样本的数量为N，对于每一个样本xn，其对应的输出为tn，其中tn为当前时刻的温度，用平方误差和作为损失函数，损失函数可以表示为：

加拿大全国气候变化趋势图如图1所示. 从多项式拟合曲线可知，自1840年到1960年期间加拿大温度呈下降趋势，1960年至今呈上升趋势，在未来可能持续上升. 因气候变化是长期作用的结果，故以10年的温度平均值来分析，结果如图2所示，1950温度代表1950～1959年的平均温度，由图2可知，在1900～1959年之间，加拿大温度整体呈现下降趋势，而1960年至今温度呈上升趋势. 本文把 1910～1919年定义为第一阶段，1950～1959年定义为第二阶段，2000～2009年定义为第三阶段.

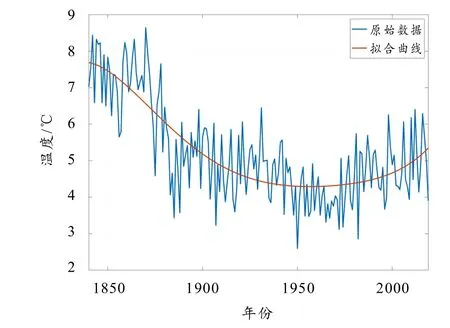
图1 加拿大全国气候变化趋势图

图2 加拿大全国气候变化趋势（每10年）

对每个阶段进行具体分析获得其空间的变化趋势如图3、4所示. 在1910～1919年和1950～1959年这两个时间段，由于加拿大北部的温度监测站还没有完全建立，导致北部区域缺少温度数据. 但从图3和图4的对比可以看出，无论是第一阶段的由热转冷还是第二阶段的由冷转热，在全国温度变暖的大趋势下，除了局部地区呈现出相反的温度变化，大部分地区符合拟合的温度变化趋势.

图3 第一阶段至第二阶段气候变化趋势

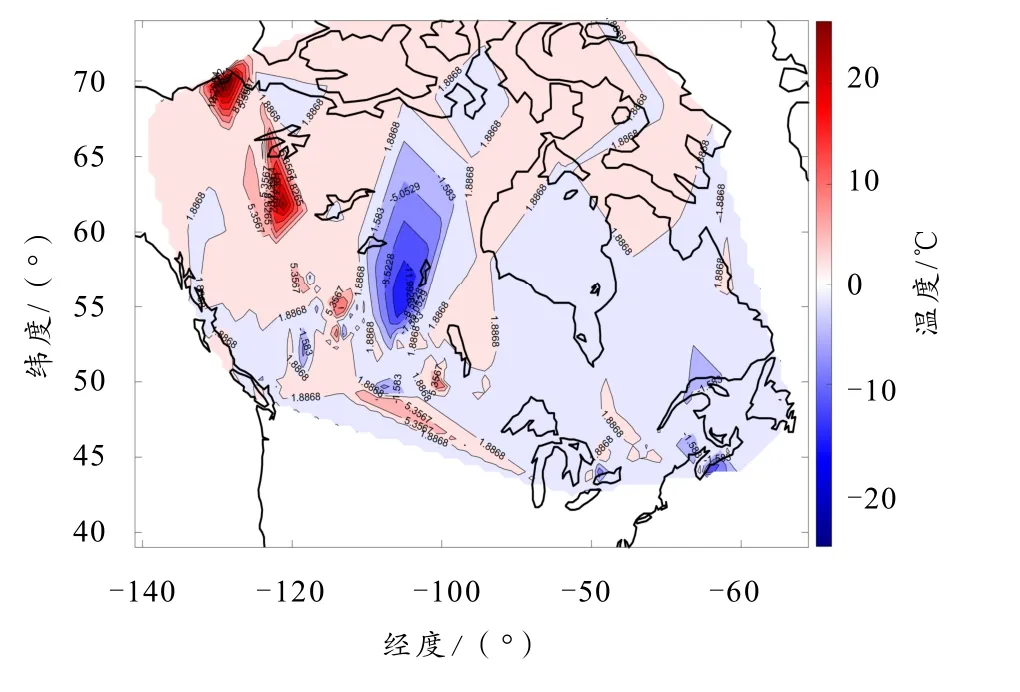
图4 第二阶段至第三阶段气候变化趋势

本文从纬度变化的角度来观察加拿大气温的时空变化，如图5所示. 图5显示了当前纬度和时间下，气温相比前一年的升降变化.图中亦表明，加拿大气候变暖在时间和空间上的分布是不均匀的. 从纬度上来看，高纬度地区的温度变化比低纬度地区的温度变化较平缓. 在 1950～2010年期间，低纬度地区的气温变化呈现剧烈的冷热交替变化；在 2010年之后，气温呈逐渐上升的趋势，符合全球变暖的预期. 这为全球变暖提供了重要的数据支撑.

图5 加拿大全国气候时空趋势变化

1.2 海洋表面温度变化趋势

对全球每年平均海洋温度进行 5阶多项式拟合，如图6所示. 拟合之后系数分别为9.255e-10，-8.952e-06，0.034，-66.958和64 715，常数项为-250 116 68. 图6表明，近100年来海洋温度在加速上升. 由于全球变暖的原因，海洋吸热可能在初始阶段对全球变暖有一定的阻碍作用，但从加速上升的趋势看，全球变暖的速率可能会大于海洋吸收热量的速率，表明全球变暖趋势不容乐观.

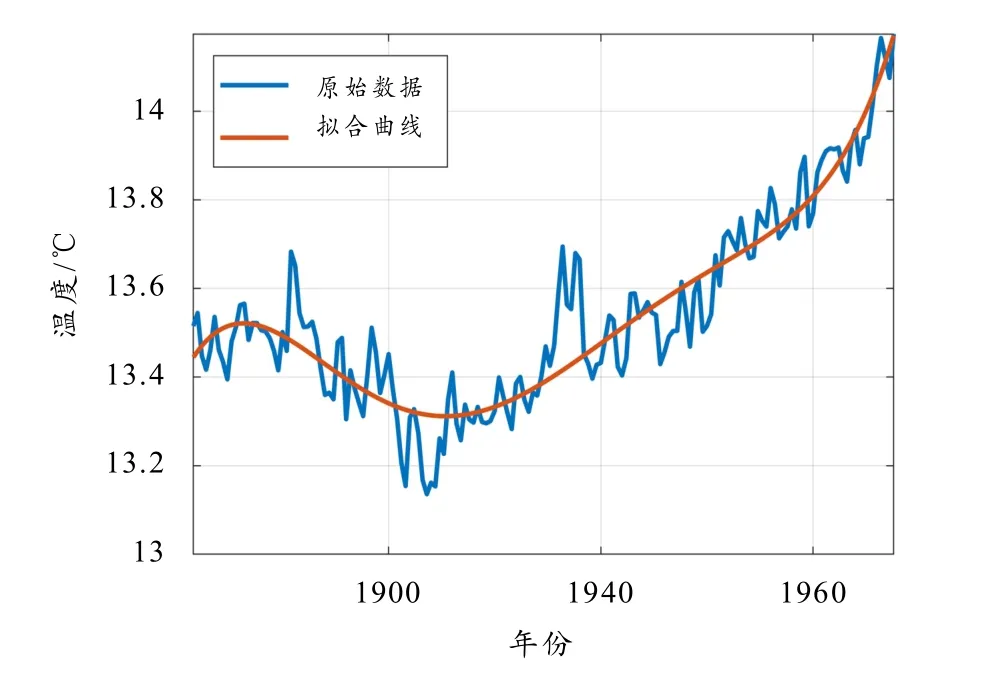
图6 海洋表面平均温度趋势

2 基于地球吸热、散热和海洋温度变化等因素的全球气候变化预测

2.1 主成分分析及相关检测

影响全球气候变化的因素很多，本文选取地球辐射[3]、海洋温度、冰川面积、二氧化碳浓度、海平面高度、降水量和陆地温度 7个特征作为主要因素. 地球散热的主要方式是长波辐射，而长波辐射在经过大气层时会被气体吸收，因此，可以用大气层顶部的长波辐射代表地球散热. 地球吸热主要来自太阳的短波辐射[4]. 假设太阳对地球的辐射量是一定的，考虑到冰川对短波辐射的反射是地球反射的主要因素，本文用冰川面积来代表地球吸热[5]. 根据上述因素的时间动态趋势进行分析，利用主成分回归分析法对各个因素进行相关性检验[6]，采用线性回归建立模型进行气候变化预测.

在主成分分析前，需采用KMO[7]和巴特利特球状检验[8]对主成分分析的可行性进行判断. 获得的KMO和巴特利特检验值如表1所示，KMO为0.801，巴特利特球形检验的显著性小于0.05，这说明各影响因子间存在显著相关性，有利于后续的主成分分析[9]. 经主成分提取后，获得的主成分系数如表2所示. 设前两个主成分分别为y1，y2，可以得出相应的线性表达式为：

从公式（3）和（4）可以看出主成分y1与海洋温度、冰川面积、二氧化碳浓度、海平面高度和陆地温度呈强相关，而主成分y2与降雨量呈强相关，故可将主成分y1归纳为非降雨影响因素，主成分y2归纳为降雨影响因素.

表1 KMO和巴特利特检验

表2 主成分分析成分矩阵

2.2 线性回归预测

本文采用线性回归进行统计分析. 假设某一因变量y受k个自变量x1,x2,… ,xk的影响，某n组观测值为，则多元线性回归模型[10]为：

式中β0,β1,…,βk为待定参数，εa为随机变量. 因此将7个大气气温自变量代入上式求解出的线性回归方程组系数分别为：0.110，0.111，-0.084，0.098 2，0.089，0.114，0.075. 绘制出的预测曲线如图7所示. 图7表明，在 1980～2018年间，预测曲线基本符合当年的气温变化情况；在 2018年后的 25年里，曲线基本呈现出稳步上升的趋势，这与全球气温变暖的大趋势一致.

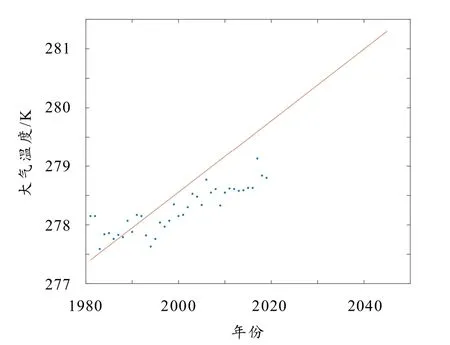
图7 大气温度变化趋势预测

3 局部极寒现象和厄尔尼诺现象的关系

厄尔尼诺现象被证明与极端天气密切相关，本文对厄尔尼诺指数和极寒天气做斯皮尔曼检验[11].斯皮尔曼相关系数被定义成等级变量之间的皮尔逊相关系数，n个影响因素形成一个n×n的相关系数矩阵，相关系数ρ为：

经计算可得厄尔尼诺指数[12]与极寒天气的相关系数为-0.265 4，说明两者之间负相关. 极寒天气与全球温度的相关系数为0.396 9，说明两者正相关，因此，说明厄尔尼诺现象与局部极寒天气有相关关系. 在全球变暖的趋势下局部地区会出现极寒现象，采用全球异常温度变化数据绘制的局部极寒示意图如图8所示.

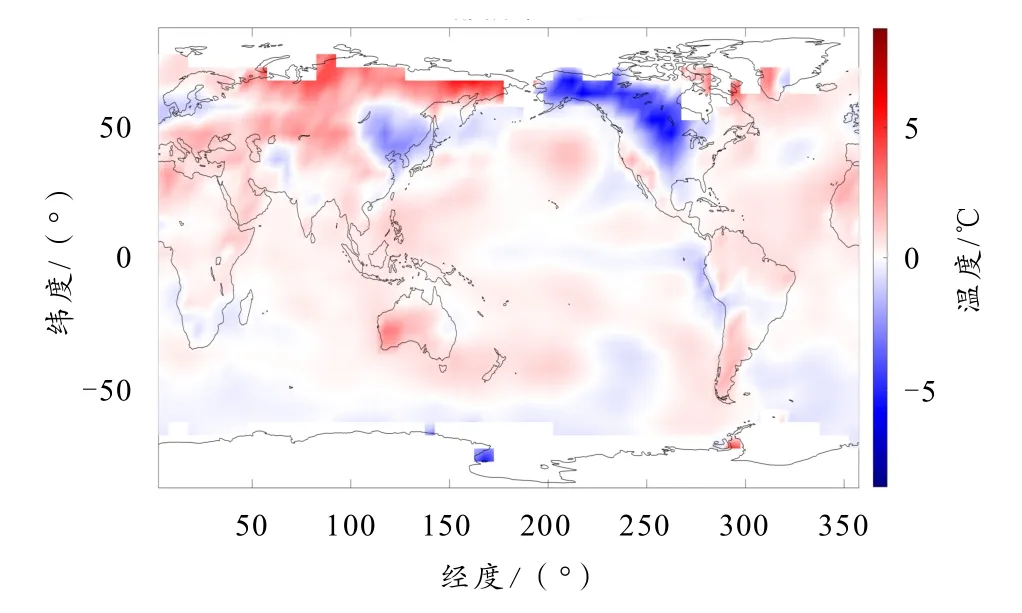
图8 局部极寒现象

4 基于变异指数的全球变暖趋势分析

据前面的分析可知，全球温度增高导致海洋温度急剧上升，尤其是低纬度的大洋. 热量形成暖流向北极方向移动，导致北极的冷空气被热空气“挤”到南方，因此，某些地区会有极寒天气出现.由前文分析可知，极端天气出现的原因跟降雨量、冰川面积、海平面高度这3个因素有很大的关系，而这 3个因素也是全球变暖的重要因素，因此提出气候变异系数，具体公式如下：

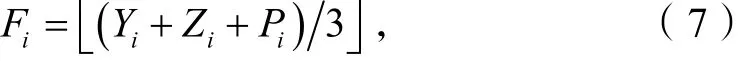
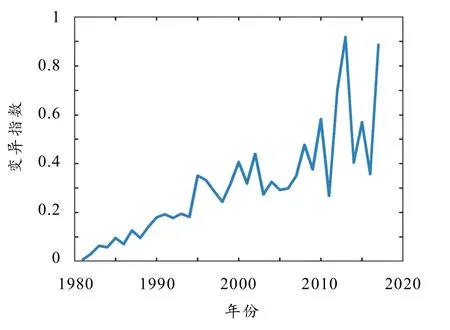
图9 全球气候变异指数

5 结论

本文从时空分布、年际变化等方面对加拿大和海洋表面温度变化进行定量分析，然后通过气温与客观要素之间的相关性建立了多变量的气温变化模型和表征全球变化趋势的气候变异指数，得到了全球变暖的数据支撑. 本论文提出的模型和气候变异指数对于预测未来几十年内全球气候变化趋势具有一定的参考意义. 目前关于极端天气气候影响因子的观测和研究还有很多不足，后续研究将引入纬度、海拔等因素为建立模型提供更好的支撑点.