城市轨道交通列车开行方案和客流控制协同优化研究

吴开信，梁艳娟，王文宪

（五邑大学 轨道交通学院，广东 江门 529020）

城市轨道交通早晚高峰期有大量客流短时间在车站内高度集聚，列车过载、站台乘客滞留等现象已呈常态，这不仅严重降低了客运服务水平，而且给运营安全带来隐患. 如何使线路运力资源得到充分利用，使运输需求和运输供给在时空上合理匹配是亟待解决的问题.

从客流控制角度进行需求管理是运营决策者短期内缓解车站拥挤问题的可行方法之一，客流控制也称“限流”，根据控制的范围可分为车站级、线路级和网络级[1]. 在车站级方面，李曼等[2]通过构建城市轨道交通车站客流状态的模态集，分析了设备设施与客流之间的非线性函数关系. 郑雪梅等[3]基于系统动力学原理通过确认客流拥堵的关键位置对控制方案进行优化设计. 豆飞等[4]以车站设备设施不同客流状态级别对应的模板云模型和实测客流状态合成的指标云模型之间的相似程度，提出客流控制触发判别方法. 局部车站调控策略主要是从站内客流承载率的阈值来判断调控的时机和强度. 在线网级联动控制方面，文献[5-7]分别从客流聚集预警值、旅客周转量、行车组织模式等角度构建沿线多车站客流协同控制整数规划数学模型. 张正等[8]提出以车站入口限流量、站台上车旅客数量和换乘站邻线间的客流流入量作为网络级控制的重要指标.

高峰期列车开行计划和客流控制的协同方案决定了运输效率和服务质量，而目前大多数文献只侧重于对其中某一方面进行研究，实际中的限流主要按车站运营管理人员的主观经验去判断和执行，缺乏科学依据. 本文从运营安全和追求效率角度，针对常态大客流提出城市轨道交通列车开行方案和多站客流控制协同优化，以解决高峰时段线路运力资源优化配置与车站容量协同利用问题.

1 模型的构建

1.1 假设条件

假设1：列车运行只考虑一个运行方向（上行或下行），所有列车从始发站按次序开出，在同一区间的运行时间相等，每个车站在任意时刻最多只接发一列列车；

假设2：列车采取站站停的停站方案，停站时间是旅客上、下车人数的函数；

假设3：相邻两列车到站间隔期间内，站厅收费区到达乘客数服从均匀分布；客流需求量及OD结构已知；出站客流不予考虑，换乘站的换乘客流可折算成相应的进站客流.

对于假设 1，城轨列车一般采取双线追踪运行，上、下行线相互独立，因此在建模分析时可只考虑其中一条正线，定义车站（站台）集合N=｛1,2,…,i,…,j,…,I｝，共有I-1个区间，车站按先进先出的排队模式接发列车，前后列车按移动闭塞安全间距保持间隔. 对于假设 2，站站停是目前国内城市轨道交通停站方案采取的主要形式；停站时间可基于相同时间段内的历史数据进行拟合. 对于假设3，高峰期常态客流通常以通勤通学为目的，乘客的工作地点和家庭住址相对固定，从i站去往j站的乘客比例xij可由AFC数据统计分析获得；出站客流对站台和站厅的拥挤影响较小，建模时予以忽略.

1.2 优化模型构建

1.2.1 行车约束条件

列车k∈｛1,2,…,K｝表示控制时间内从始发站发出的第k次列车，其在车站i的到达时刻为ak,i，停站时间为，根据假设1，列车k在两车站间[i,i+1]的运行时间RTk,i为定值，为保证列车的运行安全，设fk,i表示前车k-1与后车k在车站i的到达间隔时间，决策变量fk,1表示在始发站的发车间隔，f1,1=0，列车动态运行过程如图 1所示. 相邻两站的列车到达间隔时间有如下关系：

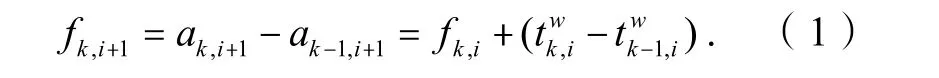
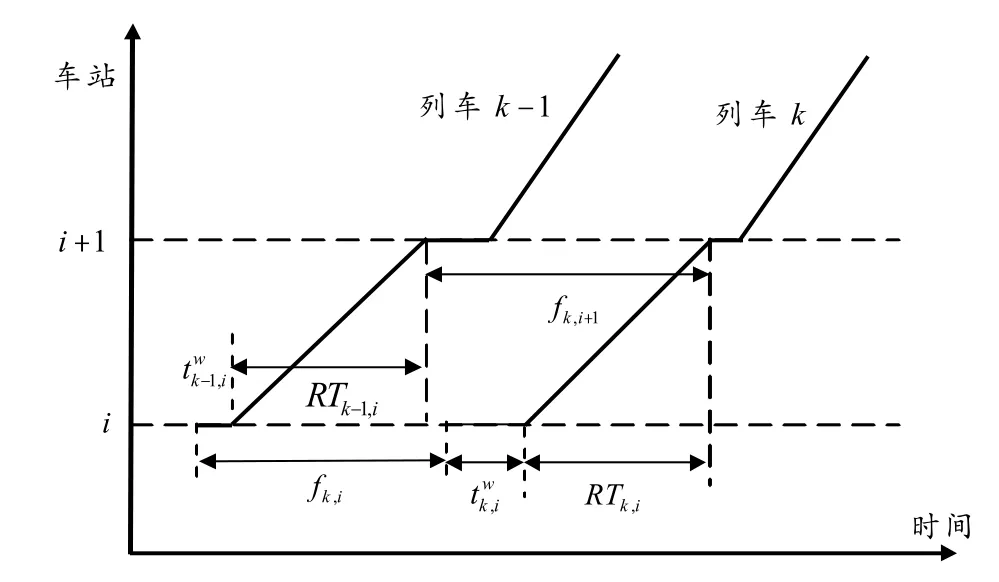
图1 列车区间运行过程

即前后列车在i+1站的到达间隔时间主要是由车站i的到达间隔时间及前后列车的停站时间决定的.在以往文献中通常作为常量，由于城市轨道交通站距较短，停站时间是列车运行周期的重要组成部分，在此将其作为决策变量之一，且是上、下车人数的线性函数，可表示为：

且满足：

式中和分别表示在站台i实际下车、上车人数，γ、γ、τ和τ为已知参数.12minmax

1.2.2 客流控制及加载过程约束

前后列车到达车站i为一个计算周期，即包括前车到达、停站、列车出发、发到间隔时间 4个阶段. 受站台容量的限制，为保证运营安全，对站厅非付费区到达乘客进行客流控制，决策变量ck,i为一个周期内的限流人数，为简化问题，忽略付费区闸机处到站台的走行距离，客流在站厅的控制过程和列车到站时的加载过程如图2所示，从图中可以看出车站乘客集聚、消散与列车运行状态之间的动态关系.

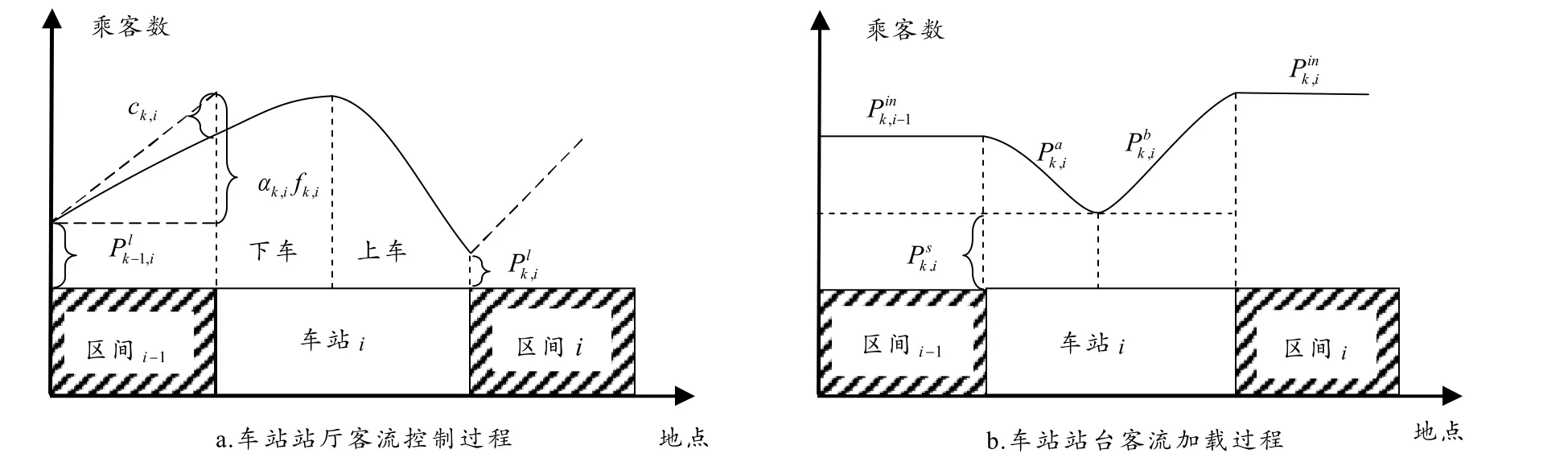
图2 列车运行状态与车站客流控制及加载过程之间关系

列车k从站台i发车时站台的滞留乘客人数、区间的断面客流量分别为：

式中α为列车到达间隔时间内乘客在站厅到达率，单位“人/s”，和可由下式得出：

k,ii

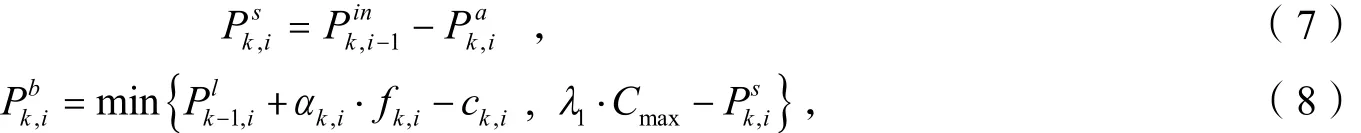
式（6）表示下车乘客数为前方所有车站上车乘客中以当前站为目的地站的乘客数之和；式（7）表示列车到站时不下车的乘客数；式（8）表示实际上车人数是由候车人数以及列车到站时的剩余运力决定的，Cmax和λ1分别为列车定员数和高峰期加载系数. 为了防止站台过分拥挤造成安全事故，假设在站台滞留的乘客皆能登上下一次列车，即：

车站i的客流控制情况如图2-a所示，受站厅通道和站台承载能力的限制，站厅内的进站人数和站台候车人数不能超过其最大容量，即：

1.2.3 目标函数

客流控制策略在保证城市轨道交通安全运营的同时，也在一定程度上增加了乘客延误，主要包括两部分：站台延误和站厅延误. 列车到达站台后，若站台上候车乘客数量小于列车空余载客能力，则不存在滞留情况，否则存在滞留. 依据式（9）的假设，乘客因无法上车而造成的滞留时间长度为本趟列车与下趟列车的到站时间间隔. 为此引入0-1变量ηk,i：当时，η=1，k,i否则为0. 则站台滞留乘客的延误时间为，在站厅因被限流而导致的乘客延误时间为：

本文以乘客的总延误时间最小化构建目标函数1：

各站站厅在任意采样周期内控制人数越少将对乘客产生的影响越小，以此构建目标函数2：

因为只考虑上行（或下行），本问题以最后一列车通过各站后，各车站总滞留人数最小化构建目标函数3：

以式（13～15）为目标函数，以式（1～12）为约束条件，构建城市轨道交通客流控制和列车开行方案协同优化模型.

2 算法分析

根据各变量特征可知，该协调优化问题模型是含 0-1变量的多目标混合整数非线性规划模型（MOMINLP）. 首先，本文采用评价函数法中的线性加权系数法处理多目标情形，即满足权重jω反映了决策者对延误时间、客流控制强度、站台滞留数的偏好程度. 其次，由于约束条件（8）是一个非凸约束，难以直接获得全局最优解. 文献[9]提出一种ICP算法（Iterative Convex Programming，ICP），即采用线性逼近、惩罚函数和近似赋值等方法处理非凸约束条件，通过迭代求解凸规划过程，使新的凸规划在保证解的收敛性的同时，逐渐逼近原问题的最优解，但针对大规模优化问题，算法的时效性有待提高. 为了降低算法的复杂度，本文提出引入 0-1辅助变量yk,i，把MINLP变为混合整数线性优化问题（MILP）进行求解. 具体算法思路如下：

1）引理[10-11]：假设不妨考虑g（x）≤0的情形，若y为0-1变量，则当且仅当时，g（x）≤0与y=1等价，其中ε是任意小的正数.

2）引入变量gk,i和yk,i：设yk,i为0-1变量，令取，则当且仅当时，g≤0 与y=1等价，同理，k,ik,i也是gk,i≥0 与yk,i=0等价的充要条件，其中ε为任意小的正数.

综上，把模型可转化为等价的单目标混合整数线性规划问题（MILP），可直接利用通用代数建模系统（GAMS）编程调用相应的求解器求解.

3 算例实验

3.1 基础数据

将本文提出的模型在8个车站、5条运行线、24个客流 OD 的小型算例中进行测试. 为确保行车安全，地铁列车在载客运营之前需安排空驶列车限速轧道，本文设f1,i=0，且=0，车站其中ko表示不停站，列车在各区间的运行时间分别为{100，200，200，100，100，100，110}，单位：s，参数人，车站i站厅旅客到达率ak,i、站台面积Si及此站上车人数在之后各站的下车比例xij如表1所示.

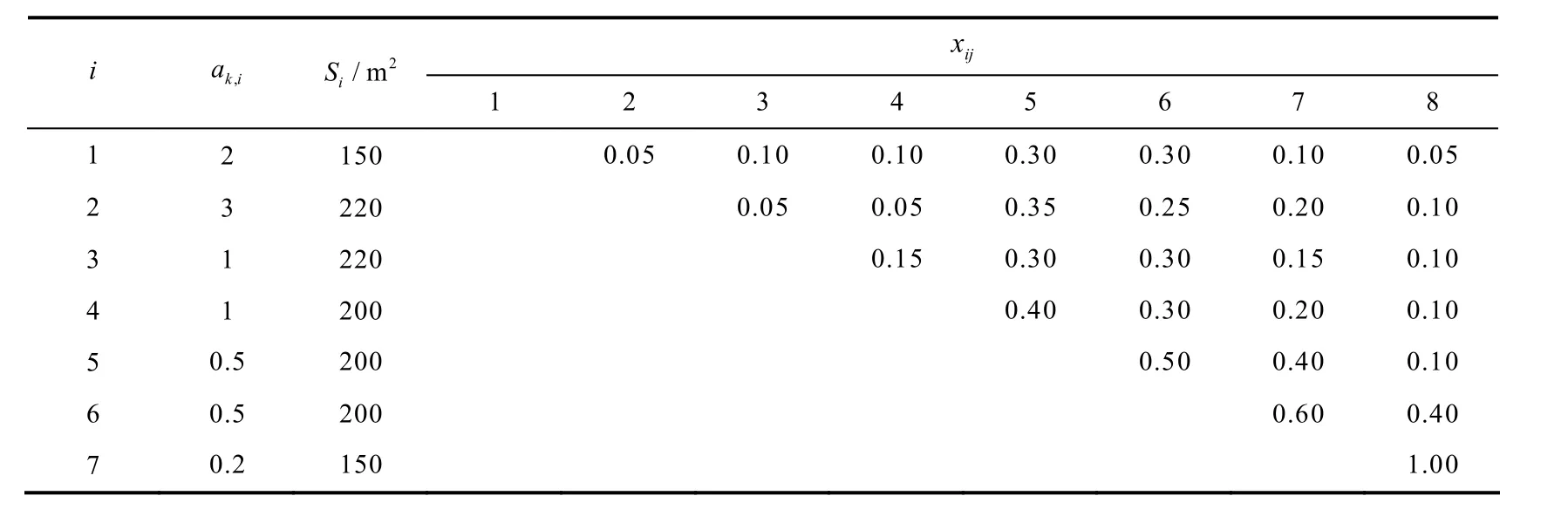
表1 站厅旅客到达率及去向分布规律

由于GUROBI在数学规划问题第三方优化器评估中展示出较好的优化速度和精度，本算例建模后利用GAMS编程调用求解器GUROBI进行求解，计算终止条件取Gap=0.5%.

3.2 结果与分析

控制方案主要包括控制车站、控制时间和控流强度3个要素. 经过52s迭代计算，得出问题的最优解，列车运行图如图3所示. 乘客的总延误时间为389138 s，各车站站厅在计算周期内需控制的人数合计1 917人次，站台滞留人数如图 4-a所示. 站台滞留客流主要集中在车站 4的站台，但在承载能力范围之内.

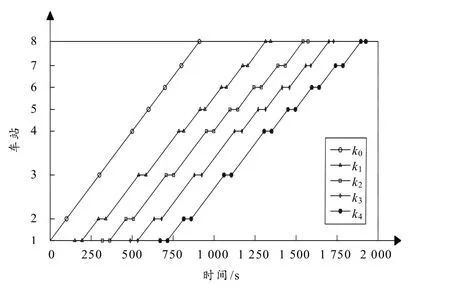
图3 地铁列车运行图

若各车站不采取控流措施，乘客的总延误时间为878348 s，增加了 126%，如图 4-b所示，以车站3、车站4站台的场景为例，不仅列车满载率在第3、4区间段都达到极限值，严重影响了车厢内乘客的舒适性，而且每列车发车后站台都有乘客滞留，随着时间的推移，滞留乘客人数呈逐步递增的趋势. 进一步计算可知，当站厅乘客到达率αk,i达到1.5倍时，两个站台的滞留人数都超过了站台的承载能力，拥堵现象特别严重，极易发生踩踏等事故.

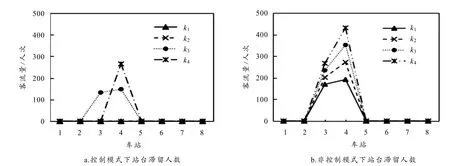
图4 不同模式下的站台滞留人数

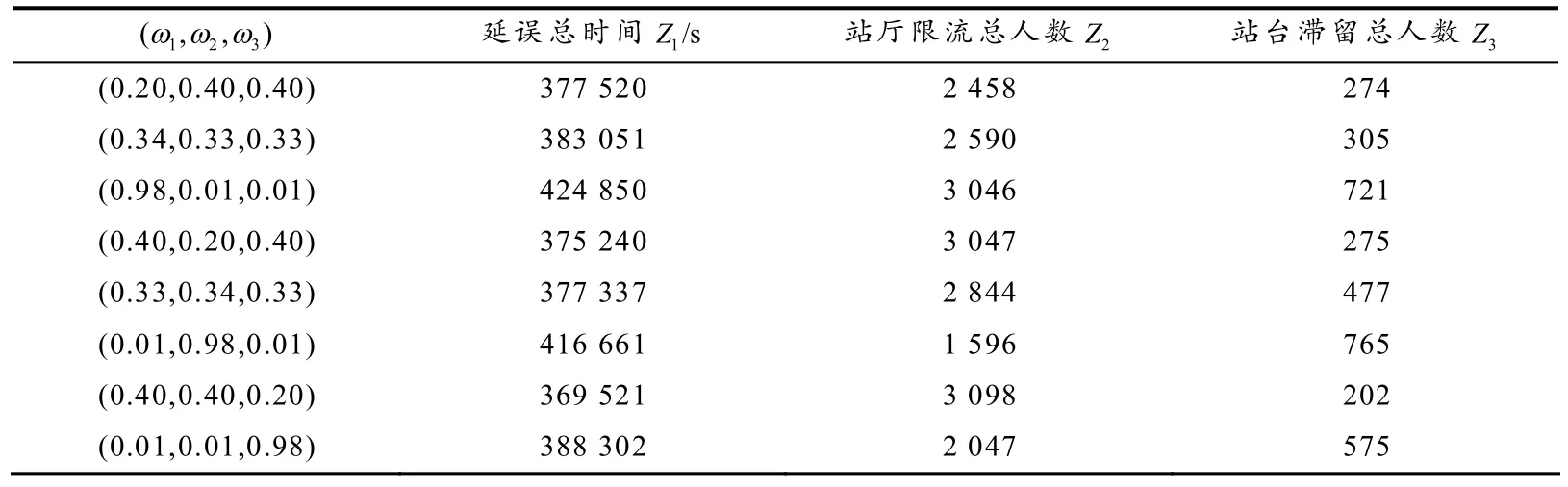
表2 目标函数不同权重下的情景分析

4 结语

城市轨道交通早晚高峰期客流拥挤，站台滞留现象严重，存在运营安全隐患. 本文在考虑乘客时空分布规律以及站台和列车承载率的基础上，通过沿线各车站站厅客流协调控制，改变客流需求分布状态，在保证车站运营安全的同时使运力资源在各车站间得到有效配置. 最后通过算例对限流车站的选择、限流时机和强度及目标函数不同权重下的限流效果作了分析.

本文仅考虑站站停、固定编组等常见的运营模式，在今后的研究工作中可考虑客流控制与多交路组合运营模式，以及为缩短列车运行周期，在不均衡系数较大的线路采取客流控制与跨站停车运行组合模式等，以应对多样性的客流需求，满足运力与客流动态匹配关系，提高服务水平质量.