一种Dual-LSTM混合模型的产线设备状态预测方法与应用

马 跃，李成蒙，尹震宇，李明时，柴安颖，赵志浩

(中国科学院大学，北京 100049) (中国科学院 沈阳计算技术研究所，沈阳 110168)

1 引 言

现如今，随着科学技术的发展，现代工业已基本实现了机械化、自动化的生产流程.在生产线作业中也越来越多地引入大型机械化设备，这些设备间一般具有先后的生产次序关系，单个设备作为生产线的一部分，其稳定性和安全性直接影响着整个生产线的持续性运行[1].一旦生产线中的设备发生故障，不仅会降低生产效率，而且可能带来严重的安全生产事故.同时，在大多情况下，设备故障并不是瞬时发生的，而是通过一定的时间累积出现的异常现象，具有一定的规律性[2].因此，如何有效地对生产线中设备的运行状态进行预测，对于做好安全生产和提高生产效率至关重要.

传统上对于设备运行状态的判断主要依靠人工经验来完成，一般根据已掌握的设备历史维护信息来判断未来一段时间内是否会发生故障，但是这种维护方式带有很强的主观性，可能会受到设备的运行强度、环境因素、人为因素等的影响；另外就是采用定时维护的方式，但是会带来“维修不足”以及“维修过剩”等问题[3].

一般来说，设备运行过程中产生的数据属于时序数据，其本质上反应的是某个或某些随机变量随时间不断变化的趋势[4].时序数据会受到各方面的影响，具体表现为数据的非线性、非平稳性、快速变换且包含噪声等特点[5].传统ARIMA(差分整合移动平均自回归)模型要求输入为平稳数据，但是现实中获取到的时序数据一般多为非平稳的，因此还需要对数据进行差分处理，使数据最终满足平稳性的要求.随着人工智能技术的发展，出现了越来越多的深度学习算法，这些算法能够很好地对非线性数据进行处理，有效地解决了ARIMA模型对数据平稳性的依赖问题.晏臻等[6]人采用CNN和LSTM相结合的方式实现了对交通流量的短时预测；冯浩等[7]人针对样本类别分布不均衡的问题，提出了一种加权焦点损失函数(WFL)，并与LSTM模型相结合，实验结果表明，这种预测模型相较于传统的机器学习算法能够更好地学习到特征在时间维度上的变化规律；陈平等[8]人基于GRNN神经网络建立了电子装备的状态预测模型，通过仿真分析，验证了模型的可行性与预测的准确性；侯晨煜等[9]人在神经网络算法的基础上，结合卡尔曼滤波，提出了一种新型有效的地铁客流短时预测算法；代杰杰等[10]人为预测电力变压器运行状态，建立了基于长短时记忆网络的电力变压器状态预测模型，能较准确地反映出变压器的优劣状况.

为了能更好地描述设备的未来运行状态，为设备维护提供及时有效的建议，本研究针对生产线设备维护过程中存在的问题，结合获取到的设备运行状态数据，采用LSTM网络结构作为预测模型对设备的状态进行初步预测.同时针对多步预测过程中存在的误差“累积”问题，采用另外一个LSTM网络结构对预测模型的残差数据进行建模，作为辅助模型对初步预测结果进行修正，可以有效降低误差传播对预测精度的影响.

2 相关理论基础

随着Hinton等[11]人提出深度学习的概念以来，诸如人工神经网络(ANN)、卷积神经网络(CNN)和递归神经网络(RNN)等逐渐被越来越多的领域所采用.深度学习相较于传统的统计学习方法，能够通过多层非线性变换，从原始数据中提取到由底层到高层、由具体到抽象、由一般到特定语义的特征[12].这种结构上的优势，让深度学习能够在计算机视觉、自然语言处理等领域中发挥较好的预测效果.

2.1 循环神经网络

循环神经网络(Recurrent Neural Network,RNN)将时序的概念引入到了网络设计中，使其能够更好地处理时序数据问题[13]，能更大限度地挖掘出时序数据间隐含的信息.循环神经网络在相邻的神经节点之间都有连接，可以用来传递数据间的状态信息，同时每个神经节点又可以接受新的状态输入，结合历史保留信息，能够预测输出下一时刻的数据状态.具体网络结构如图1所示.

图1中xt-1、xt、xt+1代表输入的时序数据，yt-1、yt、yt+1表示每个时刻的输出，可由如下公式得到：

ht=f(U·xt+W·ht-1)

(1)

yt=g(V·ht)

(2)

其中U、V、W为权重矩阵，可以被网络所共享，大大减小了网络的训练复杂度；f(x)和g(x)分别为隐藏层和输出层的激活函数，f(x)通常采用tanh(x)函数，而g(x)根据输出数据的类型来选择对应的激活函数；ht则为网络保存的历史状态，可以有效地利用数据间的关联性信息.

2.2 长短时记忆网络

虽然循环神经网络能够记忆状态信息，但是，在处理时间跨度较长的输入时会存在长期依赖问题.这是由于状态ht在接受每个输入时都会被更新，因此会失去前期输入的“记忆”，导致不能有效利用时间跨度较长的时序数据中的信息.因此，在循环神经网络的基础上演化出了长短时记忆网络(LSTM)，通过加入3个“门”和一个能保存输入“记忆”的结构，有效解决了RNN在处理长序数据时存在的问题[14，15].其细胞结构如图2所示.

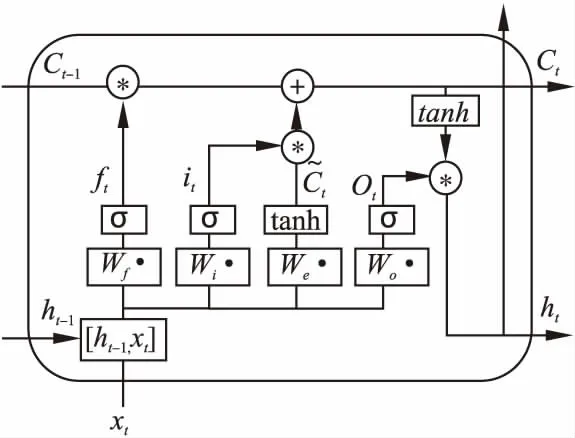
图2 LSTM细胞结构图Fig.2 LSTM cell structure diagram

1)遗忘门(forget gate)：用来控制需要保留的细胞状态信息，计算公式为：

ft=σ(Wf·[ht-1,xt]+bf)

(3)

其中[ht-1,xt]为上次输出与本次输入向量的一个拼接，Wf和bf分别表示权重矩阵和偏置项.运算结果通过一个sigmoid激活函数映射到0-1之间，决定了保留之前信息的程度.

2)输入门(input gate)：主要负责当前序列位置的输入，计算公式为：

it=σ(Wi·[ht-1,xt]+bi)

(4)

(5)

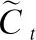
3)细胞状态更新：将遗忘门和输入门得到的数据添加到上一细胞状态中，计算公式为：

(6)

细胞状态记录了起始输入到当前输入所保留的信息，通过遗忘门信息与输入门信息进行求和运算，可以有效解决RNN中的梯度消失和梯度爆炸的问题.

4)输出门(output gate)：根据细胞状态和输入数据决定当前的输出，计算公式为：

ot=σ(Wo[ht-1,xt]+b0)

(7)

ht=ot*tanh(Ct)

(8)

其中状态输出由两部分组成，第1部分ot为上次输出和本次输入向量拼接后通过sigmoid激活函数映射得到，第2部分则由细胞状态与第1部分的输出相乘得到.状态输出有两个作用:1)作为当前时刻的预测值，2)进入下一个细胞网络中参与参数运算.

3 系统设计

根据时序数据前后相互关联的特点，通过滑动窗口的方式进行数据分割，结合LSTM循环神经网络，本节给出Dual-LSTM混合模型的数据预测方法，实现对设备状态的准确预测.

3.1 系统总体结构

系统的总体结构如图3所示.首先通过数据库或者远程推送的方式获取到设备的历史状态数据.由于设备信息采集装置处于工业环境现场，可能会受到传感器失效、网络阻塞等各种情况的影响，从而导致采集到的数据出现异常，因此需要采用一定的方法对这些原始数据进行预处理，主要包括异常值去除、缺失值补全、数据归一化等.然后对处理后的时序数据进行数据分割，以满足后续模型的输入格式要求.最后进行模型的网络参数训练，通过预测模型和辅助模型相结合的方式完成对设备状态的预测工作.

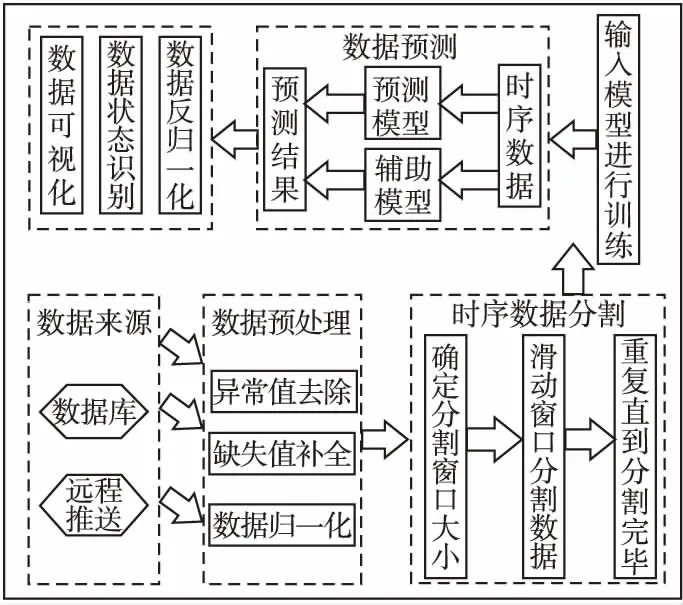
图3 系统结构Fig.3 System structure

3.2 数据集构建

为了提升模型的收敛速度以及训练精度，首先采用公式9对数据做归一化处理，将数据映射到[min,max]的区间中，一般取min=0，max=1.

(9)

其中x′为归一化后的值，x为原始值，xmax和xmin分别为数据中的最大值和最小值.通过归一化后，数据保留了原始的走向趋势，但是其值被限定在一个较小范围内，在一定程度上减小了异常值对模型的影响.对于模型的预测结果，还需要进行反归一化为实际值，反归一化的公式为：

(10)

然后在归一化后的数据基础上构建数据集，对于时序数据采用的是过去一段时间内的数据对未来数据进行预测，因此可以采用滑动窗口的方式构建数据集.具体做法为指定滑动窗口的长度为n，在原数据上以步长为1进行滑动，以窗口中的数据作为模型的输入数据，窗口的下一个数据作为预测值，不断重复这个过程，直到构建出符合要求的数据集，具体做法如图4所示.同时为了验证模型的准确性，保留最后2000个时刻的数据作为测试集，其余的数据作为训练集参与模型参数的训练工作.

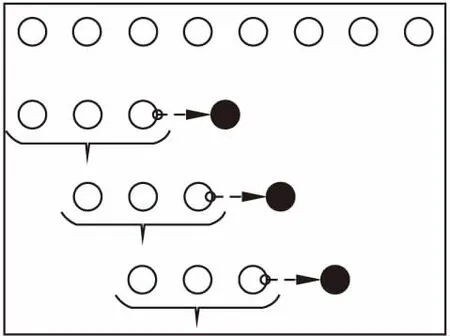
图4 数据集构建Fig.4 Construction of data sets

3.3 模型构成

预测工作主要由预测模型和辅助模型共同完成，其中预测模型主要完成对数据的初步预测，辅助模型则对预测模型的预测残差值进行确定，从而实现对初步预测结果的修正.模型均采用了第2节中提到的LSTM循环神经网络结构，主要包括输入层、隐藏层、输出层3部分，其中输入层节点个数与数据分割窗口大小相对应，隐藏层则实现对输入数据的非线性变换，输出层通过linear线性激活函数将输出映射到实数空间中.同时考虑到不同设备状态数据间的差异，可以在模型的隐藏层中加入全连接层对数据进行多维度映射.

3.3.1 预测模型构建

根据数据的特点，将分割数据的窗口大小设置为100，即每次预测需要依赖前100个时刻的序列数据，其数据格式表示为{yt-100,…,yt-2,yt-1}.同时预测模型的输入节点个数与输入数据长度相等，然后加入3层LSTM层学习数据中的隐含信息和1层全连接层进行维度映射，采用平均绝对误差(Mean Absolute Error, MAE)作为损失函数，利用自适应动量估计(Adaptive Moment Estimation, Adam)优化算法更新网络权重，并将划分好的训练集送入模型进行训练.

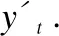
通过上述动态构建输入序列数据的方法，预测模型进行多步预测的步骤如下：

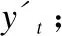
2.判断是否达到预设的预测步长，若不满足，则进入步骤3，否则，进入步骤4；

3.重新构建输入序列，加入预测值，并将新构建的序列带入步骤1中；

4.将各个预测流程中的值返回，预测结束.

3.3.2 辅助模型构建

1.将初始时间序列数据输入预测模型和辅助模型中，分别得到初步预测结果和残差预测值；

2.通过残差预测值对初步预测结果进行修正，得到更为精确的预测值；

3.判断是否达到预设的预测步长，若不满足，进入步骤4，否则，进入步骤5；

4.重新构建输入序列，加入修正后的预测值，并将新构建的序列带入步骤1中；

5.将各个预测流程中的值返回，预测结束.

4 实验验证与结果分析

为了验证本文所提出的Dual-LSTM混合模型对时序数据预测的有效性，以实验产线为目标，通过将温度传感器部署到六轴机械手伺服电机的外围壳体处，以采集到的温度数据进行实验验证，从不同的预测方式上进行结果对比，采用均方根误差(RMSE)、平均绝对误差(MAE)作为模型的预测性能评价指标.

4.1 实验准备

首先从数据库中读取已储存的温度数据，由于数据中存在一定的异常值和缺失值，因此采用线性插值算法对这些值进行替换、填充，使数据满足连续性的特点要求.然后采用第3节中的分割方法将数据划分为训练集和测试集，分别进行预测模型和辅助模型的网络参数训练.

4.2 模型单步预测效果验证

为了验证混合模型能够有效地降低预测过程中产生的误差，首先在测试数据集上对模型的单步预测效果进行验证分析，利用训练完成后的预测模型和辅助模型进行预测，与单LSTM模型预测结果对比如图5所示.

从图5中可以看出，单模型预测曲线虽然与真实值曲线趋势保持一致，但是与真实值之间还是存在一定的差距，而加入辅助模型后，由于能够对每次的预测结果进行修正，因此混合模型能够更好地拟合真实数据值，减小预测过程中产生的误差.另外从表1中的预测结果指标数据上也可以看出，混合模型在RMSE值和MAE值上均比单预测模型更低，验证了本文提出的Dual-LSTM混合模型在设备状态数据单步预测上具有良好的有效性.

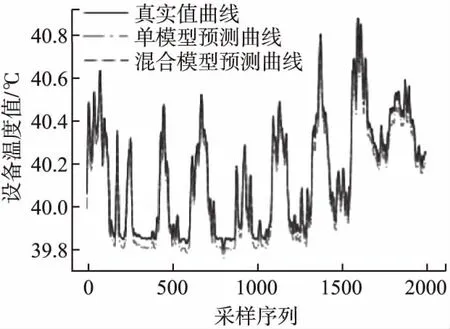
图5 单步预测结果对比Fig.5 Comparison of single-step prediction results

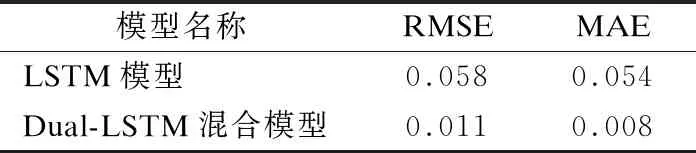
表1 单步预测结果Table 1 Single-step prediction results

4.3 模型多步预测效果验证

为了进一步说明本文提出的Dual-LSTM混合模型在数据多步预测上的有效性，利用第3节中提到的对数据循环预测的方法，在测试集上进行循环预测25个时刻的状态数据，结果如图6所示.

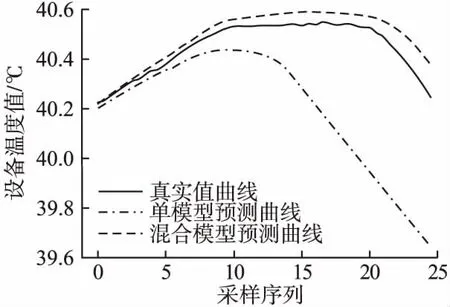
图6 多步预测结果对比Fig.6 Comparison of multi-step prediction results

由于每次在进行输入序列重建时都会引入一个预测误差值，因此单模型在预测到第7个时刻的数据时，误差的“累积”导致输入序列数据偏离了正常范围，在后续过程中已经不能准确地预测出当前时刻的真实值.而混合模型能够对每一步的预测结果进行修正，因此，在前期预测过程中引入的误差较小，预测模型依然可以进行正常预测.在第10个时刻时，

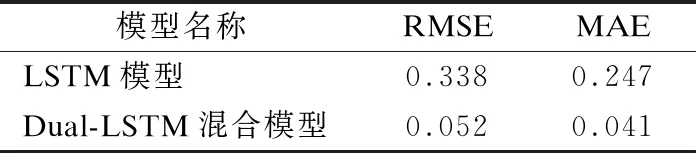
表2 多步预测结果Table 2 Multi-step prediction results

虽然预测值与真实值的差异变大，但是依然能够捕捉到真实数据的走向趋势,从表2中的预测结果指标数据对比中也可以看出，混合模型的预测精度更高.

5 结 论

本文提出了一种Dual-LSTM混合模型数据预测方法，针对时序数据预测过程中出现的误差“累积”问题，提出了一个可以对预测结果进行修正的辅助模型，并在实际产线设备数据上进行了验证，通过与单LSTM模型在单步和多步的预测结果上进行对比，实验结果表明，辅助模型能够有效提升预测精度，并在多步预测上也能有较为出色的表现效果，较大地改善了对产线设备状态预测的能力.在本实验研究的基础上，下一步的研究工作应该主要放在对状态数据的识别以及故障预测方面，通过对已有故障数据进行建模，来识别出预测数据中可能会出现的故障信息.