利用可变参数和二阶回归方法建立海南省相思树立木材积模型
2020-12-08陈怡
陈 怡
(国家林业和草原局 中南调查规划设计院,湖南 长沙 410014)
森林蓄积量指一定森林面积上存在着的林木树干部分的总材积,它是反映一个国家或地区森林资源总量、森林资源丰富程度和森林生态环境优劣的重要指标之一。立木材积表作为森林经营管理中最重要也是最常用的林业数表之一,是森林蓄积量的计量依据,同时也是森林蓄积量估测的主要误差来源之一。
一元与二元立木材积表是制定最佳森林经营措施的基本工具之一,也是长期以来林业工作者开展各项森林经营活动的度量和标尺,在监测森林资源中发挥着重要的作用。在森林资源调查监测评价中,通常采用以胸径和树高为自变量的一元、二元立木材积模型对森林蓄积进行计量。在生产中以山本材积式模型应用最为常见[1,2],该模型能较好地反映干形随胸径(D)和树高(H)变化的规律,在生产实践中普遍认为适用性好,精度较高。有学者以山本材积式为基础,对提高模型拟合效果与适用性进行了探索研究,如骆期邦等[2]、曾伟生等[3-4]等构建的可变参数动态模型和综合考虑材积与生物量的相容性建立了联立方程组模型,陈振雄等[6-7]分别采用分段建模和多元混合效应模型方法建立了橡胶树、加勒比松立木材积模型,上述改进模型与常规山本材积式相比,拟合效果更好,模型精度更高。相思树是海南省广为种植的树种之一,主要品系为大叶相思Acacia auriculiformis、马占相思Acacia mangium、粗果相思Acacia crassicarpa等,研究建立其一元、二元立木材积模型,以期为科学计量评价森林资源、完善海南省森林资源监测体系等提供重要依据。
1 数据来源
数据来源于海南省常用数表编制项目[8],共实测样木150 株,全部为人工起源。采集样木覆盖海南省东部湿润区的琼海市、文昌市,中部山区的五指山市、琼中县、白沙县、屯昌县和西部干旱区的临高县、儋州市。胸径按径级取样分为4、8、12、16、20、24、28 cm 以上7 个取样点位,在每个取样点位按高径比控制选取样木。样木数据采集时,首先将选定的样木进行伐前胸径、地径和10 cm 高度处直径测量,伐倒后将所有枝丫砍掉后,量测树干总长度(H)和树干相对高0.05H,0.1H,0.2H,0.3H,0.4H,0.5H,0.6H,0.7H,0.8H,0.9H处带皮直径。
树干材积采用区分求积法[1,9]计算得出:
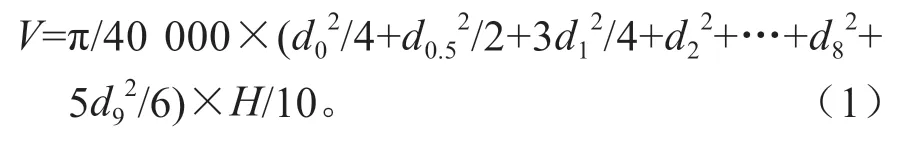
式中:di(i=0,0.5,1,2,…,9)分别表示0,0.5/10,1/10,2/10,…,9/10(H)处的带皮直径(cm);H为树高(m);π 取3.14159。
得到建模样木按径级分布情况见表1。

表1 海南相思树建模样本径阶分布情况Table 1 Distribution of diameter classes of modeling samples of Acacia spp.in Hainan province
2 研究方法
2.1 二元立木材积模型
2.1.1 山本材积式模型
对于主干材积而言,山本材积式能较好地反映干形随胸径和树高变化的规律,因此,树种材积模型的建立选定山本材积式作为基本模型,模型结构式[2]为:

式中:V为立木材积(m3),D为胸径(cm),H为树高(m),c0为模型固定参数,c1、c2为模型待求参数。
2.1.2 可变参数动态模型
立木材积模型误差大小和效率高低不仅与两个解释变量的选择有关,而且与变量的体现形式及模型参数是否可变有关。树木干形变化随胸径和树高变化的速度不一样,并且有着复杂的变化规律,为反映材积随胸径和树高变化的客观规律,提高模型预估精度,本研究中的动态模型以山本材积式为框架,将山本式的参数设计成胸径和树高的函数式,得到可变参数动态模型结构[2]如下:
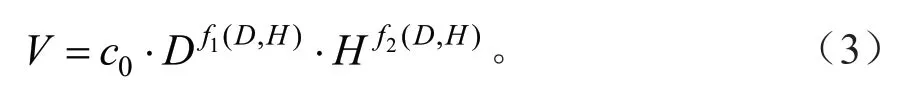
要确定fi(D,H) 的具体模型结构,先固定已拟合得到的(2)式固定参数c0,再把式(2)待求参数c1、c2看成是与形数有关的参数,分不同径阶、不同树高阶按方程式(2)拟合,求解得到不同径阶、不同树高阶对应的参数c1、c2值,再做出c1、c2值随不同径阶、不同树高的散点图,分析确定c1、c2与D、H的相关关系函数式,从而得到相思树可变参数动态模型结构如下:

式(4)中:V为立木材积(m3),D为胸径(cm),H为树高(m),c0为模型固定参数,c3-c4·(D+H)、c5+c6·(D+H) 中c3、c4、c5、c6分别为模型待求参数。
2.2 一元立木材积模型
2.2.1 常规模型
一元立木材积常规模型采用如下结构[10]:

式中:V为立木材积(m3),D为胸径(cm),Ci为模型参数。
2.2.2 采用二阶回归方法建立一元材积模型
采用以树高—胸径模型为基础的二阶回归方法来建立各树种树高一元材积模型,该方法主要基于以下三步来考虑[11]:
第一步,对树高—胸径数据进行分析,选取合适的树高—胸径模型结构式:

第二步,利用建模样本数据,采用加权回归拟合二元山本材积式模型(7),求出参数值a、b、c:

第三步,固定参数a、b、c值,将树高—胸径模型式(6)代入二元立木材积模型式(7),利用建模样本数据拟合求出模型f(D)的参数值:

此方法实际上就相当于设计出了一个更为复杂的材积—胸径模型,只要式(6)的树高—胸径模型选择得当,一元材积模型式(8)就会比式(5)做出更加符合客观规律的描述。
根据上面的思路,分析得到相思树采用如下树高—胸径模型结构式:

将上述树高—胸径模型结构式代入模型(8),得到相思树一元胸径材积模型结构为:
模型式(10)中参数a、b、c值直接采用式(2)中建立的二元山本材积式拟合结果,c7、c8、c9为相思树树高—胸径模型待求参数。
2.3 异方差处理
由于立木材积等数据普遍存在着异方差性,在求解模型参数时必须采取措施消除异方差的影响,常采用对数回归法或加权回归方法。加权回归方法的权函数选择一般有两种:一是模型本身为权函数进行加权回归,它是相对误差为等方差时的最优权函数,能得到参数的无偏估计值;二是根据普通最小二乘法回归结果的残差平方拟合与树高的回归关系,再用权函数进行加权回归。本文采用加权回归的方法,每个方程的权函数采用模型本身确定。
2.4 模型评价方法
为了对建立的模型拟合效果进行科学检验与评价,本研究采用如下评价指标:确定系数(R2)、标准误差(SEE)、预估精度(P)、总相对偏差(TRB)、平均系统偏差(MSB)和百分标准误差(MPSE)[12-14]。其中,R2、SEE是回归模型的常用指标,P是反映平均估计值的精度指标(可视为估计林分水平的精度指标),TRB和MSB是反映拟合效果的重要指标,二者都应该控制在一定范围内,趋向于0 时效果最好,MPSE是反映平均单株林木材积或质量估计值的精度指标。根据《一元立木材积表编制技术规程》,总相对偏差(TRB)要求控制在±3%范围以内,建立的数学模型有效。
3 结果与分析
3.1 二元立木材积拟合结果与分析
以模型本身的倒数为权函数进行加权回归,得到相思树山本材积模型式(2)和可变参数动态模型式(4)的拟合结果见表2。从表2中可以看出,无论是采用山本材积式模型或可变参数动态模型,拟合的结果都较好,确定系数(R2)均在0.98 以上,平均预估精度(P)均在98%以上,两模型均具有较高的确定系数(R2)、较小的标准误(SEE)、稳定的模型参数和较高的预估精度,模型拟合结果良好。且可变参数动态模型相比山本材积式模型确定系数、平均预估精度进一步提高,可变参数动态模型拟合程度优于山本材积式模型。
对山本材积式模型和可变参数模型进一步分径阶进行检验,结果如表3所示。从表3中可以看出,建立的山本材积式模型和可变参数动态模型整体总相对偏差(TRB)和平均系统偏差(MSB)均在±3%以内,这表明从整体上看,两种模型都不存在明显系统偏差。对各径阶进行分析,山本材积式模型在8、20 cm 径阶总相对偏差(TRB)和平均系统偏差(MSB)均超出了±3%范围,而可变参数动态模型各径阶总相对偏差(TRB)和平均系统偏差(MSB)均在±3%范围以内。可变参数模型在各径阶上总相对偏差(TRB)和平均系统偏差(MSB)指标基本都优于山本材积式模型,尤其对于大径阶和小径阶效果更加明显。

表2 二元立木材积模型拟合结果Table 2 Fitting results of binary tree volume model
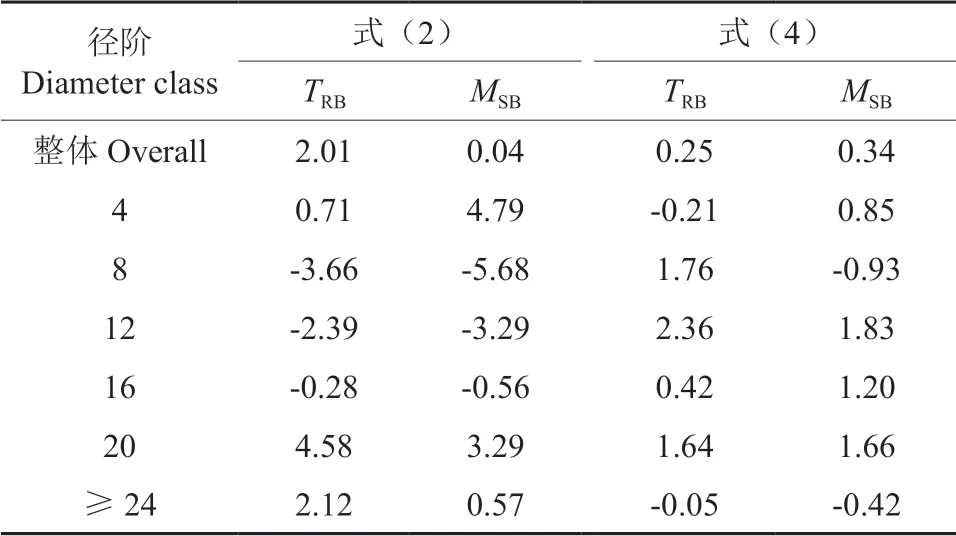
表3 二元立木材积模型分径阶检验结果Table 3 Test results of binary tree volume model by diameter classes
3.2 一元立木材积拟合结果与分析
采用非线性加权回归方法,以模型本身的倒数为权函数进行模型拟合,相思树一元立木材积常规模型式(5)和二阶回归模型式(10)拟合结果见表4。从表4所列统计指标来看,利用二阶回归方法建立的相思树一元材积模型式(10)的拟合效果和预估精度与常规模型(5)相差不大,模型的确定系数(R2)均在0.94 以上,预估精度(P)均在96%以上。两模型均具有较高的确定系数、较小的标准误、稳定的模型参数和较高的预估精度,模型拟合结果良好。

表4 一元立木材积模型拟合结果Table 4 Fitting result of one-way stand volume model
对一元立木材积常规模型式(5)和二阶回归模型进一步分径阶进行检验,得到检验结果见表5。从表5中可以看出,采用二阶回归建模和常规建模2 种方法得到的一元材积模型,总体相对偏差(TRB)、平均系统偏差(MSB)都在±3%以内,但采用常规方法建模,12、16、24 cm 以上径阶的总相对偏差(TRB)均超出5%范围,16 cm 径阶甚至达到了9.57%。而采用分段建模和二阶回归建模方法建立的模型更能真实地反映了材积随直径大小变化的客观规律,不仅可有效控制材积估计的总相对偏差、平均系统偏差趋近于0%,而且能有效控制各径阶的材积估计偏差,仅16 cm 径阶的总相对偏差超出±5%范围(为6.80%)。上述说明采用二阶回归方法建立的一元胸径立木材积模型拟合效果明显优于常规模型。
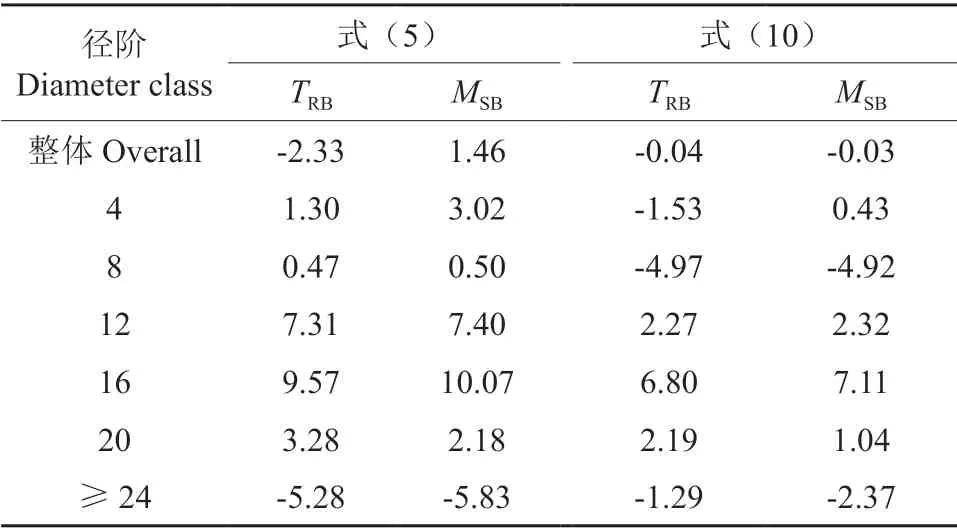
表5 一元立木材积模型分径阶检验结果Table 5 Test results of one-way stand volume model by diameter classes
4 结论与讨论
本研究以海南省相思树为研究对象,建立了以胸径和树高为自变量的二元山本材积式模型、可变参数动态模型,采用常规幂函数式和以树高—胸径模型为基础的二阶回归估计方法建立一元胸径立木材积模型,并对建立的一元、二元立木材积模型拟合效果进行了对比分析和检验。有如下主要研究结论:
1)建立的相思树二元山本材积式模型和可变参数动态模型均取得了比较好的拟合效果。在整体上,山本材积式模型和可变参数材积模型的确定系数均在0.98 以上,平均预估精度均在98%以上;在各径阶下,山本材积式模型总相对误差在±3.0%以内,8 cm、20 cm 径阶的总相对误差和平均系统误差超出±3%的范围,存在一定偏差。而可变参数材积模型总相对偏差在±3%以内,且各径阶总相对误差和平均系统误差均能控制在±3%以内。总体上无论是山本材积式模型,还是可变参数模型均具有较高的精度,具有较好的模型切合性能,可变参数模型对于大径阶和小径阶上总相对偏差和平均系统偏差指标明显优于山本材积式模型。
2)常规模型与采用二阶回归方法建立的一元立木材积模型的确定系数均在0.94 以上,预估精度均在96%以上;在各径阶之下,采用分段建模和二阶回归建模方法建立的模型仅16 cm 径阶的总相对偏差超出±5%范围,而常规方法建模较大部分径阶的总相对偏差、平均系统偏差存在明显的偏差。总体上常规模型与采用二阶回归方法建立的一元立木材积模型均具有较高的精度,二阶回归模型在各径阶上总相对偏差和平均系统偏差指标基本都明显优于常规模型。
在材积模型的提出和选择上,长时间以来,人们一直都在提出和改进材积模型。本研究对山本式材积模型和可变参数动态模型的拟合效果进行了对比分析,发现相较于山本材积式模型,可变参数动态模型拟合精度更高,各径阶误差更小,明显优于山本材积式模型。这与不少学者的研究结论相同,如候长谋等[15]分别以山本式固定参数模型和可变参数山本模型建立了广东省杉木树种的二元立木材积模型,研究表明可变参数山本模型具有更优的适用性能;贺鹏等[16]以海南松树为研究对象,以山本材积式为模型基础,建立固定参数和可变参数二元立木材积模型,研究发现两个模型的总体预估精度均较高,在各径阶上,可变参数材积模型具有更好的全面切合性能,可变参数材积模型明显要优于固定参数模型。这是由于树干材积随胸径和树高而变化的变化率与两个自变量的量值相关,可变参数模型能更为客观地反映材积随胸径和树高变化地规律,因而提高了模型的预估精度。此外,还有学者采用多元、多项回归方程和迈耶方程[17]对材积模型进行拟合,虽然精度较好,但可变参数能更为充分地利用样木信息,产生符合生物学规律的曲线。因而利用可变参数二元立木材积式编制材积表是提高立木材积表精度的一个有效途径,可变参数材积模型应作为生产上首选的二元材积模型,也是今后模型改进的方向。
本研究表明利用分段建模方法和二阶回归方法建立的一元材积模型在各径阶上总相对偏差和平均系统偏差指标基本都小于常规方法,这反映出二阶回归方法建立的模型全面切合性能更好,精度更高,各径阶误差更小。不少学者也得出了相同的结论。如曾伟生等[18]利用此种方法建立了西藏自治区四旁树阔叶树的一元立木材积模型,证明了利用二阶回归估计法比一般使用的利用树高曲线方程代入二元材积模型得到一元材积模型精度高而且能有效改善各个径阶拟合效果。有学者[18-19]将其归因于一元胸径立木材积模型未考虑树高因子,二阶回归估计方法树高曲线方程代入二元立木材积模型,利用建模样本的数据再次对模型进行拟合,这样便直接利用了材积进行拟合,可以很方便地对材积模型的拟合精度进行控制,进而客观反映材积随胸径大小变化的规律。此外,也有学者采用胸径-材积Logistic 衍生模型[20]对一元材积进行拟合,虽然精度不高,但在特定条件下,这些模型具有其他材积模型难以比拟的意义。因此,二阶回归模型可作为生产上优先采用的一元立木材积模型。
模型的检验与评价是关系到二元材积表精准与否的关键步骤。本研究采用确定系数、标准误差、预估精度、总相对偏差、平均系统偏差和百分标准误差作为模型评价指标,并运用了分径阶检验的方法,可以非常全面直观地反映各个模型的优劣,为模型检验、最优模型的选取提供了比较客观的判断标准。
由于一元(胸径)控制下的材积变动很大,其对样地水平乃至小区域范围的估计,不可避免地会产生很大的偏差,在生产中可结合相对树高曲线模型使用,以提高一元材积的适用性。
