一种移动机器人路径规划新算法
2020-12-08朱宏辉王嘉豪
朱宏辉,王嘉豪
(武汉理工大学 物流工程学院,武汉 430063)
0 引言
轮式机器人是通过驱动电机带动轮子转动来使得机器人发生移动行为的机器人,由于其具有结构简单、控制方便、模型易建、承重大、自重轻、行走速度快等特点,在生活、物流、交通等领域应用最为广泛。路径规划是移动机器人完成各种功能的基础,具备路径规划能力的移动机器人才真正具备实用性。机器人路径规划是在已知自身位置和目标点或者目标区域的条件下,在机器人运动空间寻找一条能够无碰撞抵达目标点或者区域的线路[1-3]。路径规划能够极大地扩展移动机器人工作空间,提高移动机器人的实际应用价值。
传统的路径规划算法有:Dijkstra算法、A*算法、蚁群算法、粒子群算法等。Dijkstra算法简单,但搜索速率较慢,耗时较长。A*算法通过启发式图搜索方式寻找起始点到终点之间的最低代价路径,降低了算法的复杂度,提高了算法效率,但算法对启发式函数选取较为严苛,且随着场景规模的增大,算法运行空间呈指数增长。蚁群算法与粒子群算法等仿生学路径规划算法易与其他算法结合,但算法运行效率低,不能满足移动机器人实时性要求,且容易陷入局部最小值。这些传统算法效率低下,求解困难,且无法应用于高维复杂空间[4-5]。
1998年,LaValle等提出快速扩展随机树(rapidly-exploring random tree,RRT)算法[6],它通过不断在状态空间随机性选取样本点并进行选择来规划一条可行路径[7]。RRT算法无需对状态空间显式建模,规划速度快且能够考虑机器人的各种约束,这种算法能够很好解决复杂环境下的路径规划问题。相比其他算法而言,RRT算法适用于高维复杂空间的路径规划问题,且算法路径搜索效率更高。不过,RRT 算法也存在一些缺陷,如收敛速度缓慢、路径节点冗余等[8-9]。2000年,Kuffner和LaValle等提出了RRT-connect算法,提高了节点的扩展效率,并于第二年提出双向搜索树(Bidirenctional-RRT)算法,由起点和终点同时延伸搜索树,寻找最优路径。2011年,Karaman等[10]提出RRT*算法,通过优化节点扩展方法使得算法具备概率完备性,随着采样点的不断增加,总能在空间中寻找一条由起始点到可到达点的路径。同时,RRT*算法那还具备渐进最优性,通过增加采样点逐步优化规划的路径,但是这种算法在复杂场景下冗余节点较多,且收敛时间较长。2013年,M.Jordan和A.Perez提出了将双向扩展的思想同RRT*算法结合的B-RRT*(Bidirenctional-RRT*)算法,加快了算法的收敛速度,但是算法在扩展过程中缺乏方向性并且规划路径距离障碍物过近[11]。2015年Qureshi A H等人使用智能样本插入函数使得算法快速收敛到最佳路径[12]。
针对RRT*算法在室内应用场景下规划路径存在较多冗余路径点导致移动机器人移动过程中出现多次停顿及转向的问题,本文提出一种基于局部逆序试连的路径优化策略的改进RRT*算法,通过局部逆序试连法剔除冗余路径点,缩短了规划路径长度,且提高了算法运行速度,避免了实际应用中冗余路径点导致机器人在转弯过程中出现多次停顿和换向现象。
1 RRT*算法原理
RRT* 算法是在RRT算法基础上进行了相应的改进,而使其保留算法概率完备性的同时,还具备渐近最优性的显著特征[13]。RRT算法虽然提升了路径搜索效率,但是由于节点扩展过程中的随机采样,导致路径规划过程的不确定性,算法运行效率时高时低。相同起始点和终点的条件下规划路径差别较大,可复用性差,同时规划路径往往与最佳路径偏差较大。由于RRT算法获取的最终路径并非全局最优路径,Karaman和Frazzoli提出RRT*算法来解决这个问题[14]。RRT*算法同样采用随机采样方式扩展随机树,但其在新产生路径节点附近寻找更优的父节点,以保证从起点到新路径点的路径代价为最小,然后对随机树进行重布线。RRT*算法通过寻找最优父节点和随机树重布线来不断优化路径,使得整个路径规划过程渐进优化。算法的实现原理如下:
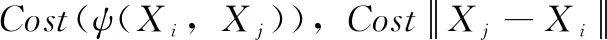
RRT*算法寻找节点的方法如下:首先将起点Xinit作为根节点放入随机树中,构建初始随机树T1。然后,通过随机函数在安全区域Cfree内获取一个随机点Xrand,并在随机树中寻找与Xrand距离最近的节点Xnearest。令步长为ρ,在Xnearest与Xrand连线之间寻找一点Xnew,使得Xnearest与Xnew之间的欧几里得距离为ρ。如果Xnearest与Xnew连线没有与障碍区域Cobs相交,则将Xnew作为新的路径节点放入随机树T中,形成新的随机树。重复上述过程,随机树扩展过程如图1所示。
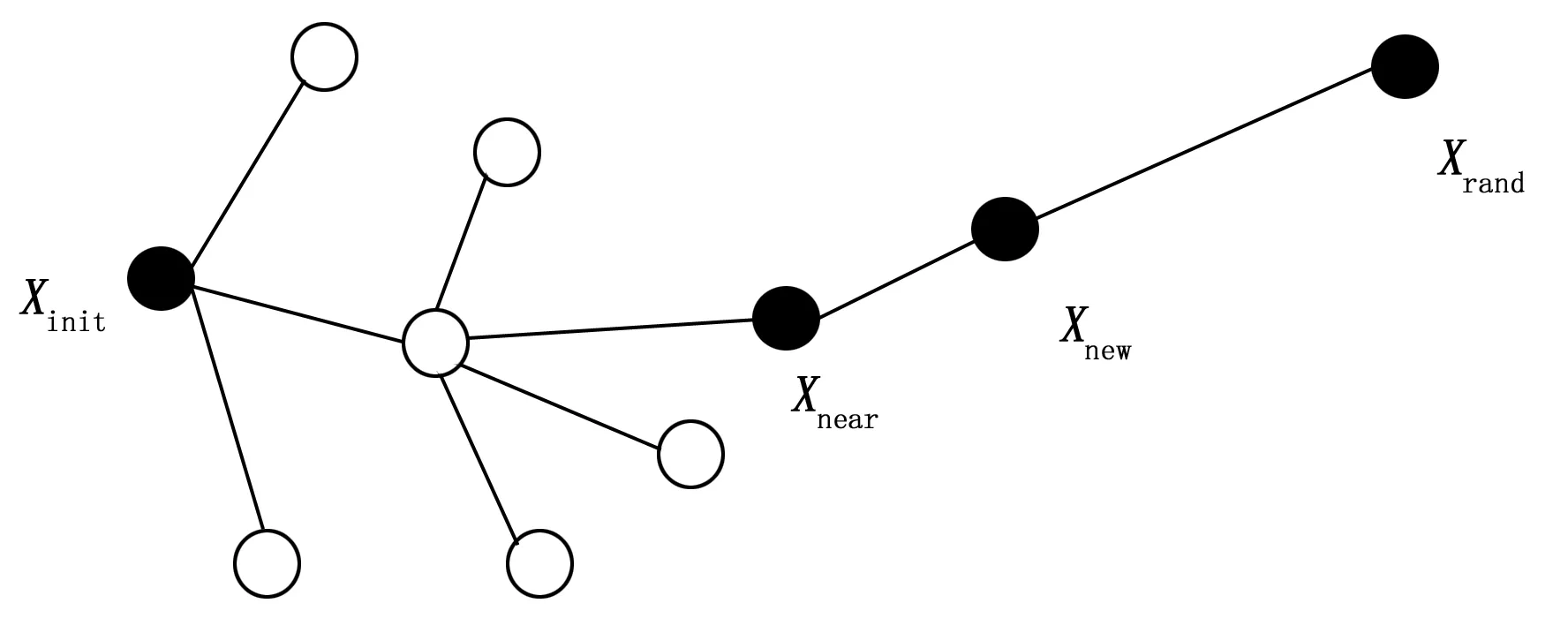
图1 随机树节点扩展
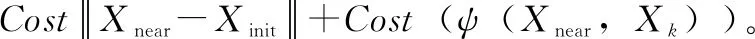
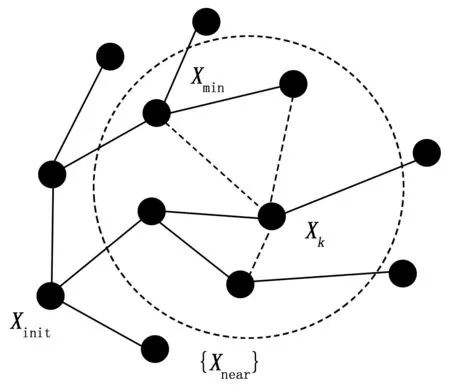
图2 随机树扩展k次后
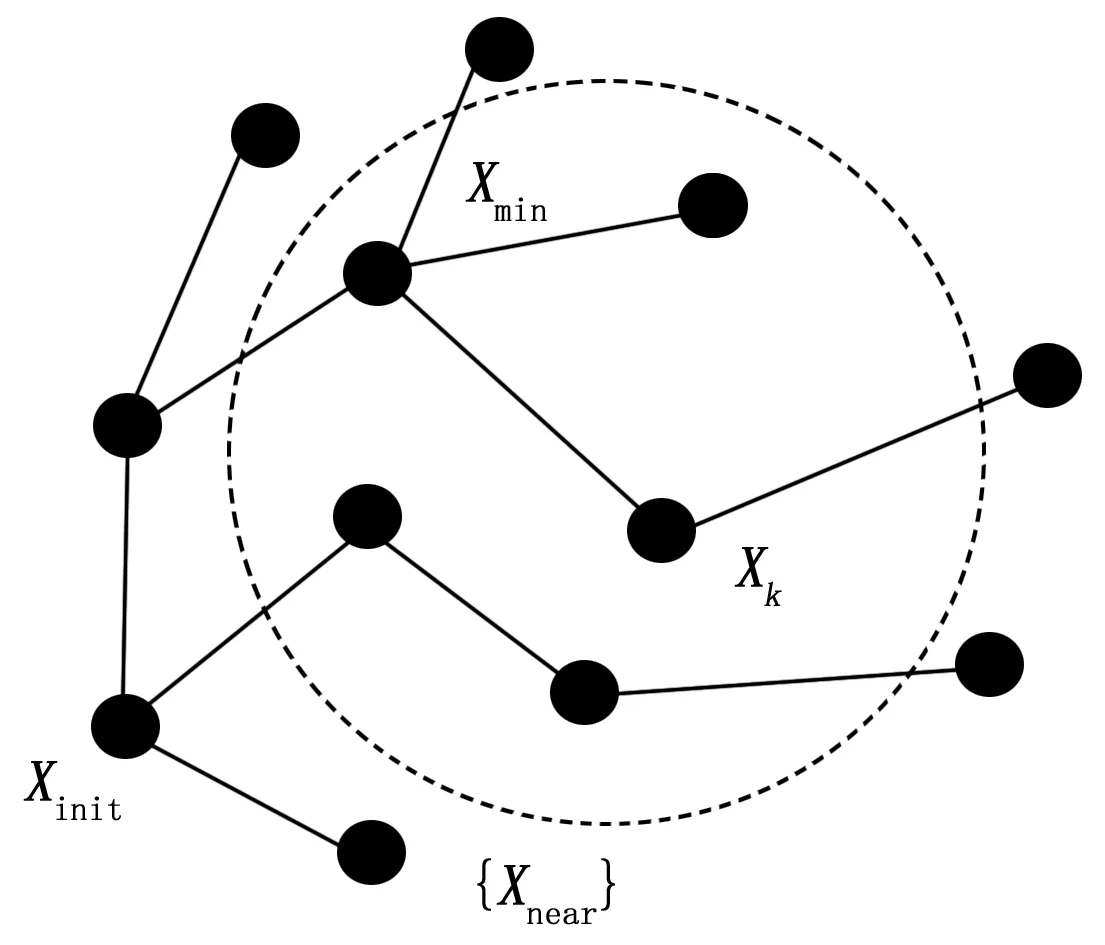
图3 选择最佳父节点
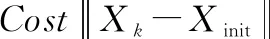
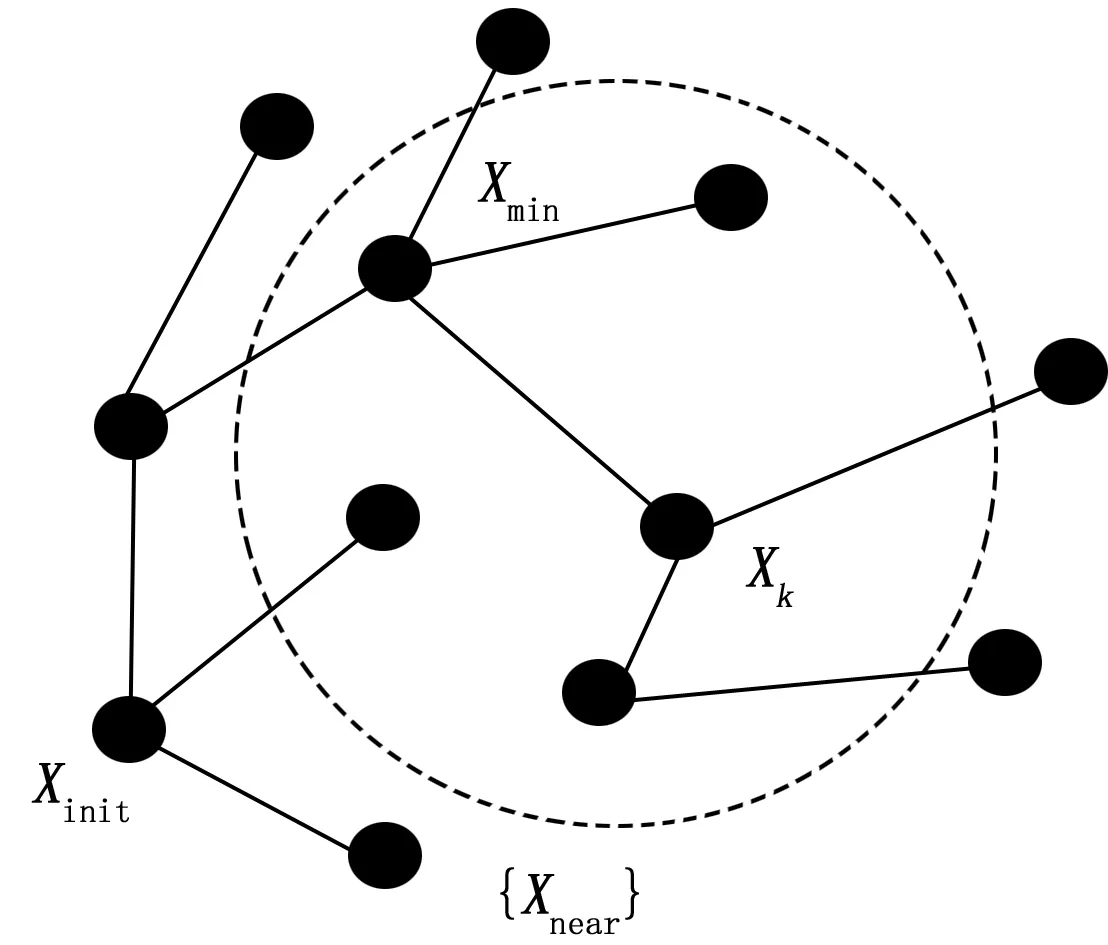
图4 随机树重布线
重复上述随机树扩展和优化过程,直到新的路径节点Xnew与目标路径点Xgoal距离在允许范围内,迭代终止。每一次迭代过程中,若随机树重连后任一路径节点连线与障碍区域相交,则放弃随机树重连,直接进入下一次迭代过程。
原始RRT*算法伪代码如表1所示,由原理分析可知算法存如下问题:采样过程中在全局区域随机生成采样点,导致在生成路径中存在大量冗余路径节点,尤其在转向部分路径。

表1 RRT*算法伪代码
2 RRT*算法改进
RRT*算法通过不断寻找最佳父节点和随机树重连来逐渐优化路径,但是因为在迭代过程中对全局状态空间进行采样,产生了大量没有必要的节点,特别是在转弯部分的路径,如图5所示。产生的冗余节点不仅降低了算法的收敛速度,还导致算法在实际应用中使得机器人在运动拐角处产生多次停顿和换向运动,降低了机器人运动的流畅度。
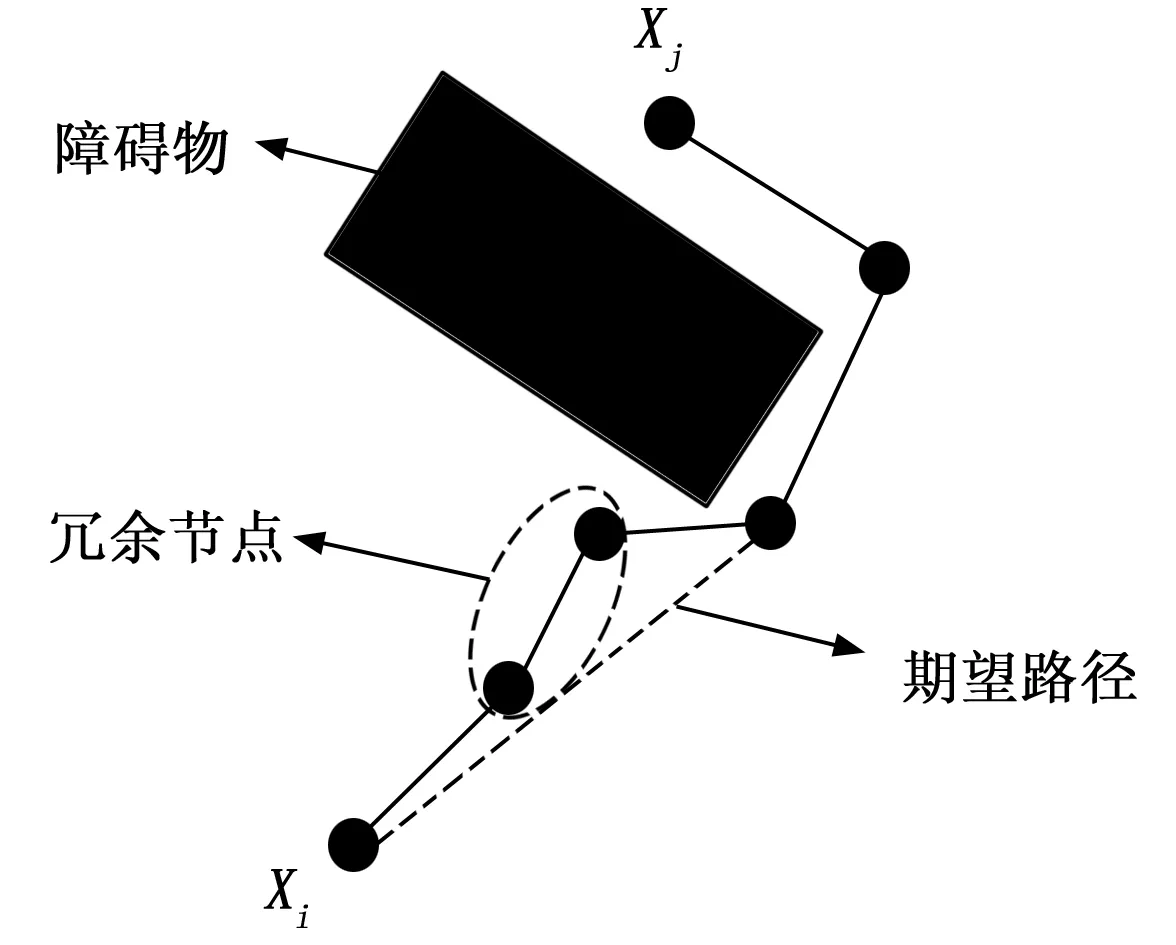
图5 规划路径中的冗余节点
在实际应用场景中,由于RRT*算法规划的路径中在障碍物附近的拐角处产生了许多冗余节点,导致移动机器人在拐角附近运动时,产生多次停顿并换向。这种现象导致移动机器人的运动流畅性差,同时降低了机器人的运动效率。同时,移动机器人频繁停顿和转向产生的机械冲击将增加移动机器人各机械部件的性能损耗,缩短了机器人的机械寿命。为避免这种现象出现,本文提出一种局部逆序试连的方法对RRT*算法规划的路径进行优化,通过局部逆序试连法剔除规划路径中的冗余路径节点,从而缩短规划路径的长度,使得转向部分路径更加平滑。在实际应用场景中减少移动机器人停顿和转向的次数,可以提高移动机器人的运动流畅性,延长机器人机械寿命,缩短规划路径,算法流程如下:
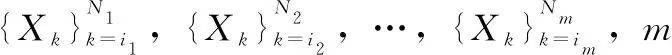
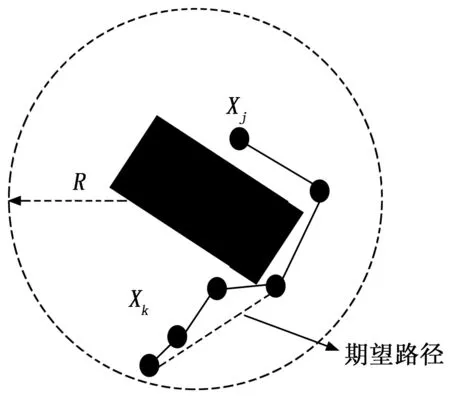
图6 局部逆序试连
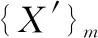
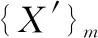
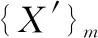
4)将得到的更新节点集合替换原始的节点集合,并以更新节点集合中的节点替换随机树中原始节点集合中的节点,即完成了一次局部路径平滑。使用下一个节点集合替换此时的节点集合,重复上述步骤,进行下一次局部路径平滑。
5)利用更新路径节点集合中所有节点依次替换扩展随机树T中与障碍物距离小于等于R的节点,将更新后的扩展随机树T′中的路径节点依次连接,即可得到最终的规划路径。
通过引入局部逆序试连路径优化方法,有效剔除了RRT*算法规划路径中的冗余路径节点,缩短了规划路径长度。改进后的RRT*算法在移动机器人路径规划实际应用中,能够规划出更接近最优路径的路径,且能够避免移动机器人在转向时候出现多次停顿和换向,使得移动机器人运动更加流畅。
3 实验与结果分析
为了验证对原始RRT*算法改进的有效性和性能更优,首先需要通过仿真软件进行路径规划模拟实验。仿真实验平台为安装在64位Windows7系统(电脑配置:Intel Core处理器,主频3.7 GHz,内存32 GB)上的MATLAB 2018a。仿真实验中在不同状态空间条件下分别使用RRT*算法和改进后RRT*算法进行路径规划实验,通过分析在相同条件下两种算法得到的规划路径的对比结果,验证算法改进的有效性。仿真实验中模拟地图大小为1 000×1 000,S表示机器人起始位置,G表示目标位置,黑色阴影区域表示障碍区域,白色区域为安全区域。
RRT*算法的随机采样步长和邻域半径决定了算法的收敛速度和路径的准确度,适当减少搜索步长和邻域半径可以提高算法的准确性,但同时降低了搜索效率[15]。实验中将随机采样步长设置为25,邻域半径为50,以使得路径规划实验效果最佳。在相同状态空间条件下,分别使用RRT*算法和改进的RRT*算法进行20次路径规划实验。路径规划过程中迭代次数越多,表示规划路径所用时间越长[16],通过对比两种算法规划路径所用迭代次数和规划路径长度可以直观地比较两种算法性能优劣。
在相同状态空间中使用不同的RRT改进算法进行路径规划仿真实验,通过对比不同路径规划算法的仿真实验结果,分析比较算法性能,仿真实验中各算法计算得到的规划路径如图7所示。其中图7为RRT-Connect算法规划的路径,由路径规划结果可知该算法搜索效率较高,但其规划路径会出现与理想路径有较大的偏差的现象。图8为B-RRT*算法路径规划仿真结果,其路径规划过程中搜索效率更高,且收敛速度更快,但是路径在局部区域容易出现与障碍物贴近的情况,在移动机器人实际应用当中容易出现碰撞事故,不适合直接用于室内服务机器人的路径规划。图9中RRT*算法规划路径与B-RRT*算法生成的路径相似,但其生成路径与障碍物能够保持一定的距离,更适合移动机器人实际使用。但是RRT*算法规划的局部路径存在较多冗余路径点,导致规划路径曲折,同时收敛速度较慢。通过局部逆序试连方法对RRT*算法进行优化,可以得到冗余转折节点大幅度减少的平滑路径,并使得路径缩短,如图10所示。增加障碍物种类,使用改进后的RRT*算法再次规划移动机器人运动路径,如图11所示。实验结果表明,在增加障碍物数目和种类的情况下,改进后的RRT*算法仍能够正确规划路径,且规划路径更接近最优路径。
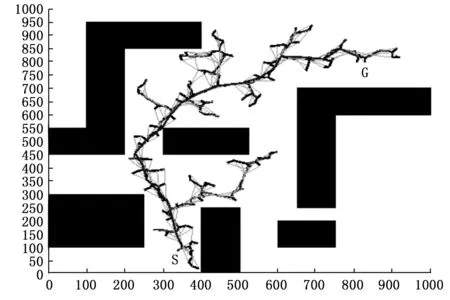
图7 RRT-Connect算法规划路径
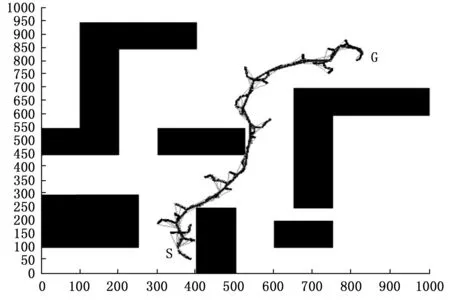
图8 B-RRT*算法规划路径
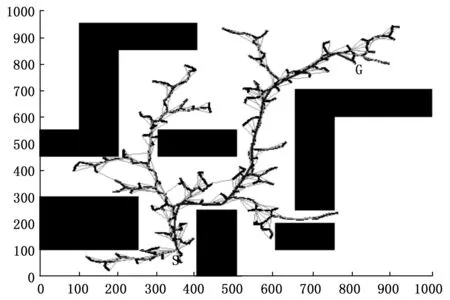
图9 RRT*算法规划路径
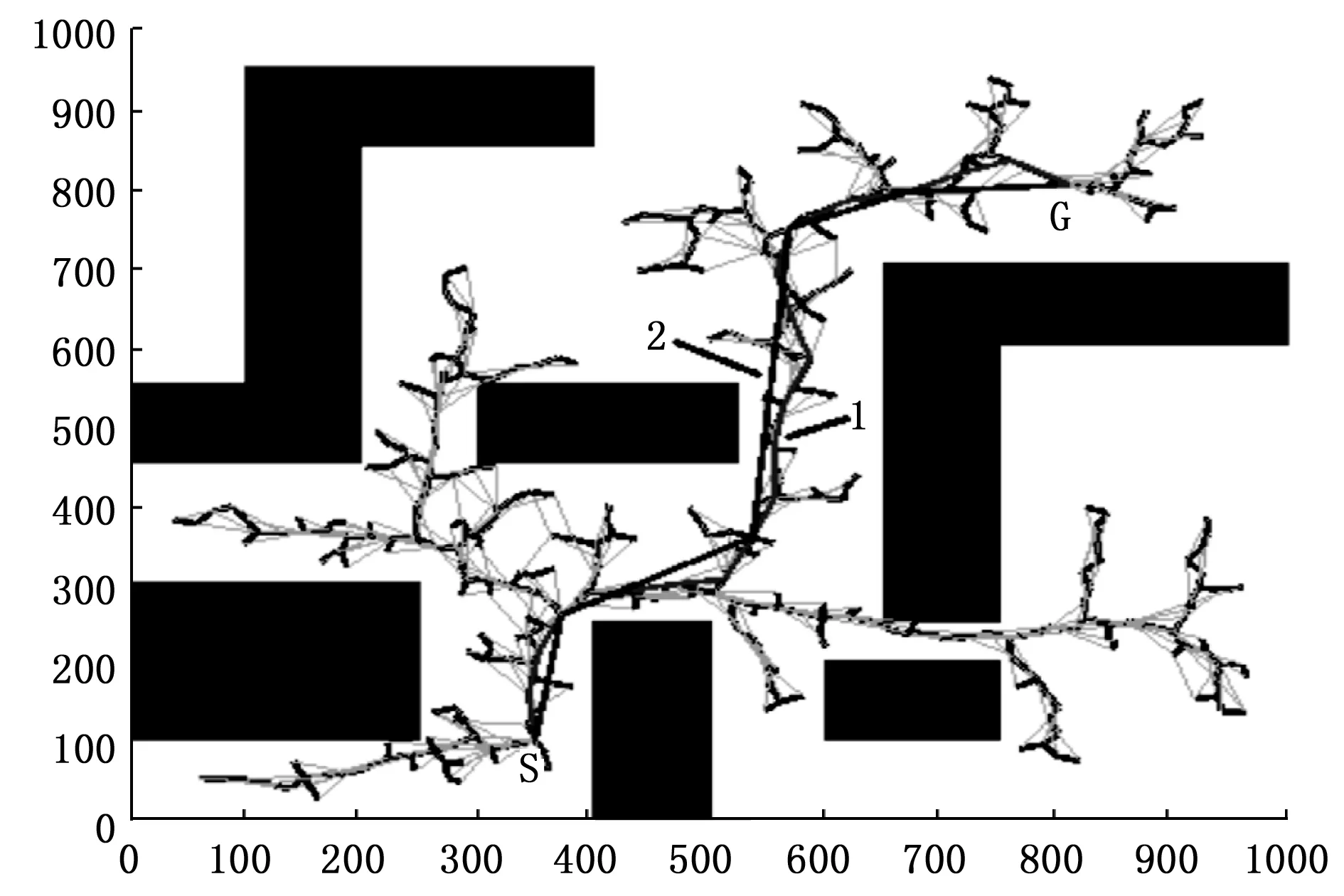
图10 RRT*算法与改进算法规划路径对比(单一种类障碍物)
图10和图11中路径1为原始RRT*算法规划路径,路径2为改进后的RRT*算法规划路径。由观察可知,改进后的RRT*算法的规划路径中冗路径节点远少于原始RRT*算法生成路径中冗余路径节点数目,不仅有效缩短了规划路径的长度,同时使得规划路径更为平滑。
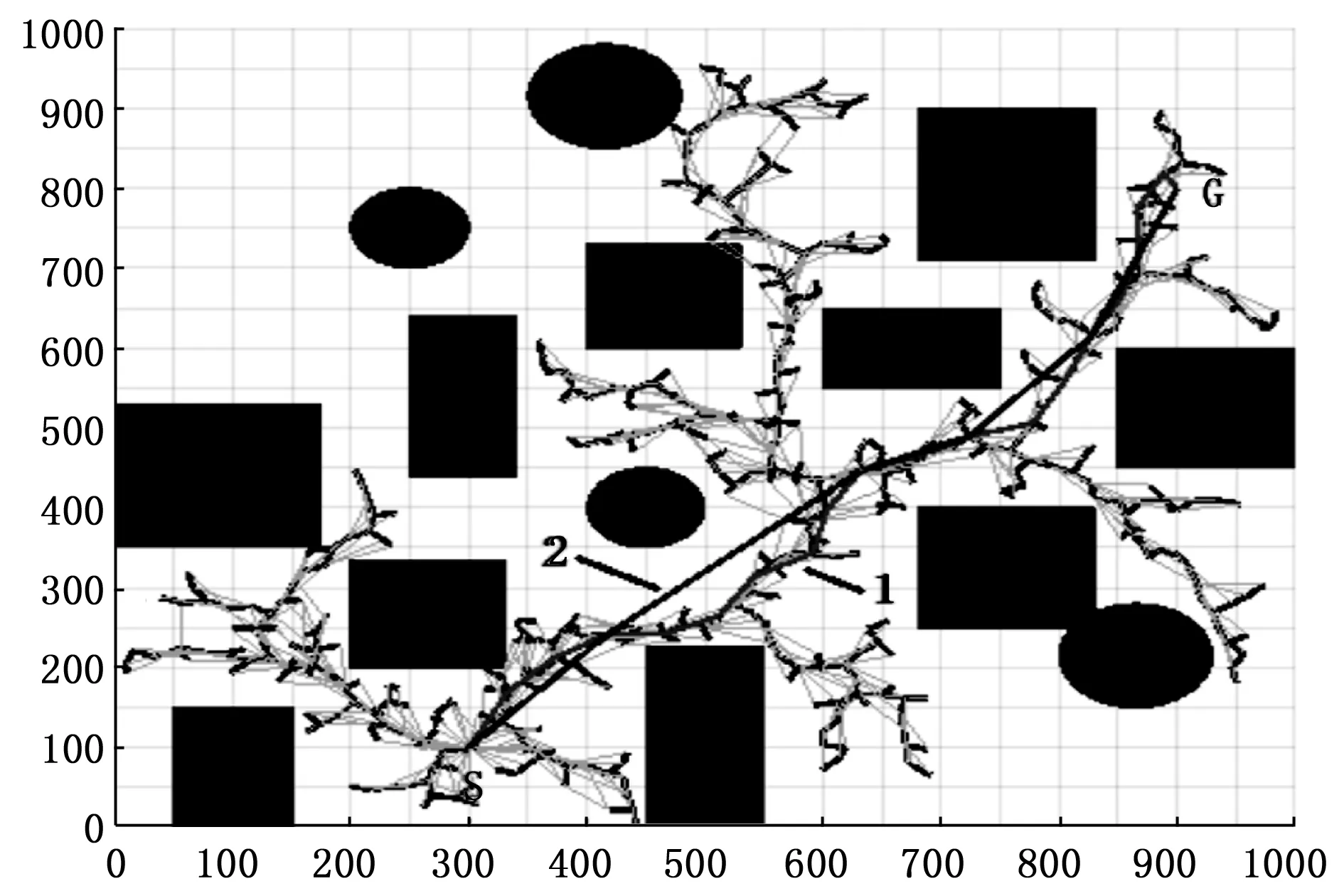
图11 RRT*算法与改进算法规划路径对比(多种类障碍物)
图12为RRT*算法改进前后在多种障碍类型区域下的实验数据对比结果折线图。由折线图可知,改进的RRT*算法路径规划过程所需迭代次数更少,并且在任意状态空间条件下其规划路径长度也更短。仿真实验数据统计结果如表2所示 ,统计结果表明在不同状态空间下改进后的RRT*算法平均迭代次数减少了38%左右,平均规划路径长度缩短了4%左右,算法耗时减少35%左右。
由仿真实验结果可知,改进的RRT*算法保留了原始RRT*算法概率完备性和渐进最优的特点,成功剔除规划路径中的冗余路径节点,缩短了规划路径的长度,使得路径规划结果更接近最优路径。
为进一步验证改进RRT*算法在实际应用中的正确性和实用性,使用该算法进行移动机器人路径规划实验。实验所用移动机器人为X2BOT V2.0,实验环境为一般室内
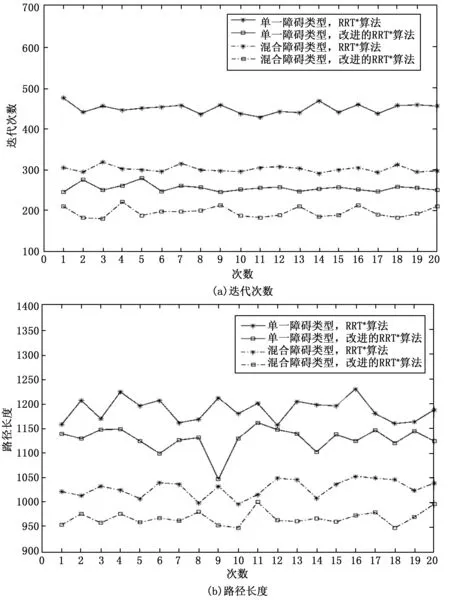
图12 两种算法实验数据对比结果
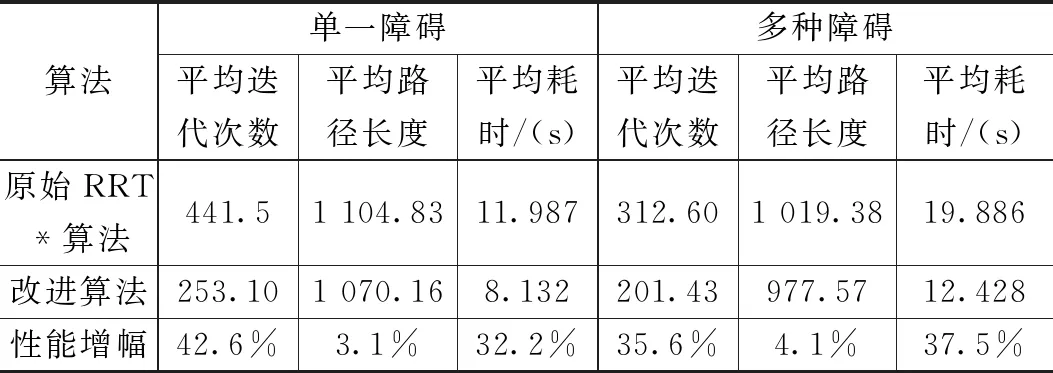
表2 实验结果对比分析表
房间,如图13所示。上位机为安装Ubuntu18.04系统的笔记本电脑(Intel Core处理器,主频2.6 GHz,内存8 G),程序运行环境为ROS。图14为机器人在控制软件中的路径规划图,图中箭头表示机器人在环境地图中的起始位置,实心方块表示目标点,算法生成的规划路径由若干路径节点构成。从图14中能够看出,机器人规划出的路径较为平滑,规划路径中没有多余的路径点。移动机器人在转弯过程中,没有出现停顿和多次转向的动作,机器人从起始点到目标点整个移动过程运动流畅。实验结果证明,改进的RRT*算法通过逆序试连法剔除规划路径中的冗余路径节点,在实际应用中能够有效避免移动机器人在移动过程出现多次停顿和转向动作,提高机器人运动连贯性。

图13 X2BOT V2.0实物图
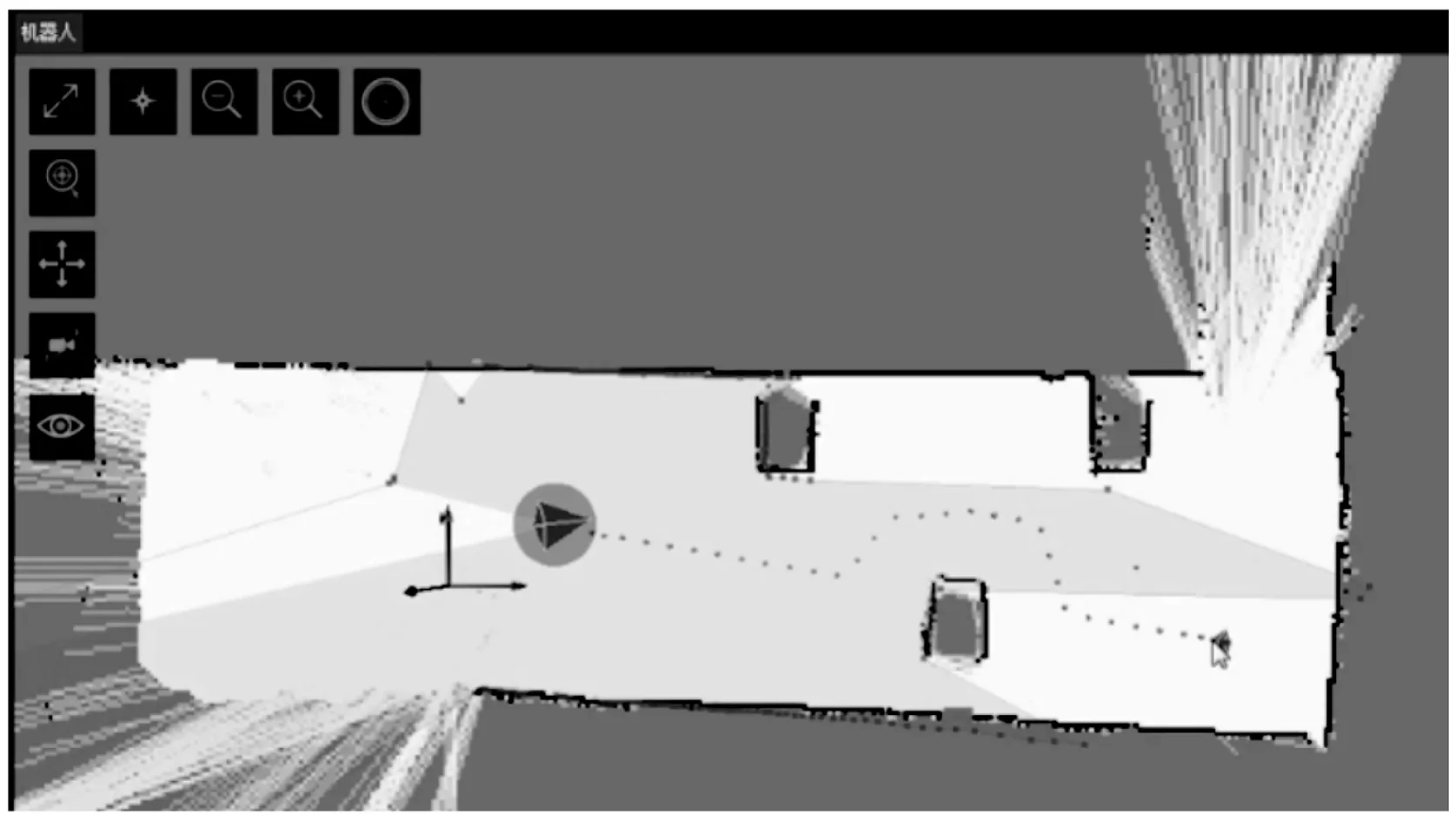
图14 移动机器人路径规划
4 结束语
RRT*算法能够规划一条较为接近最短的可行路径,但是生成路径存在大量不必要的冗余转折节点,导致机器人移动不连贯和实用性差。为此,本文提出的一种改进RRT*算法,通过引入局部逆序试连策略,能够减少规划路径中的冗余节点,缩短路径长度,使得规划路径更加平滑,更适用于室内移动机器人路径规划。仿真实验和机器人路径规划实验表明,改进后的RRT*算法规划的路径更接近最优路径,且路径规划耗时更少。在实际应用中,能够有效避免移动机器人在转向区域出现多次停顿和换向,保证机器人移动连贯性。
