基于拓扑单向波导的电磁诱导透明效应研究
2020-12-08袁庆斌
袁庆斌
(1.上海理工大学 上海市现代光学系统重点实验室,上海 200093;2.上海理工大学 光电信息与计算机工程学院,上海 200093)
引言
最早将拓扑概念引进光学系统中的是Haldane等[1]和Raghu等[2],他们发现,在有法拉第效应的旋电介质构成的六角晶格光子晶体中,电磁波可以实现类似量子霍尔效应的单向传播模式。其产生的原因类似于电子体系:在六角晶格中,狄拉克点的简并是由时间反演对称性和空间反映对称性保护的,因此,通过破缺系统的时间反演对称性来打开狄拉克点,可以实现光学系统的拓扑相变。然而,自然界中存在的旋电材料对时间反演对称性破缺的响应不大,实验上很难观察到稳定的单向传输的边界态。因此,Wang等提出采用旋磁介质来替代旋电介质[3],通过打开具有二次型的能带交叉点来实现拓扑相变。这个方案随后就在实验上得到了验证[4],并给人们后来在基于磁性光子晶体的拓扑光子系统中的电磁波调控提供了一个重要的研究方向。Fu等分别从理论和实验上研究了不同的波导宽度对单向边缘模式的影响[5]。Liu等提出,利用具有非互易磁表面等离子激元的波导结构能够设计出完美的电磁波单向吸收器[6]。Liu等研究了两个独立的拓扑光子态在双通道磁性光子晶体中的反向相互耦合效应[7]。Yang等通过调节波导两侧磁柱的尺寸以调控色散结构,实现了受拓扑保护的单向慢光态[8]。Skirlo等在大陈数波导中提出了具有单向性质的功率分配器[9]。Liang等研究了磁可调的三端口向环形器[10]。Li等基于错位磁光光子晶体结构和利用“双拓扑态结构”实现了低维的光捕获[11]。
以上这些成果说明,通过磁性光子晶体中的单向边缘模式对电磁波进行调控具有广阔的应用前景。本文是在拓扑保护耦合谐振腔波导中研究电磁诱导透明(EIT)效应的物理特性。耦合谐振腔波导中电磁诱导透明效应的产生有两种物理途径:一种是一个波导辐射共振腔(明模腔)与一个非辐射共振腔(暗模腔)进行直接耦合[12];另一种是两个失谐的共振腔通过波导间接耦合[13]。本文采用第一种途径实现单向拓扑波导中的EIT效应。我们在磁性光子晶体构成的单向波导的一侧加入两个谐振腔,通过调节谐振腔的位置,可以改变其谐振频率。由于两个谐振腔的共振模式之间的相干相消,实现了具有单向特性的电磁诱导透明效应。
1 EIT效应基本原理与模型设计
1.1 EIT效应基本原理
电磁诱导透明最早发现于三能级原子系统中[14],是光与物质媒介相互作用中电磁场与原子能级系统之间产生的一种量子干涉效应。图1为电磁诱导透明三能级模型,整个三能级系统由|0〉基态,|2〉亚稳态和 |1〉激发态组成。在图1中,当强度较弱且频率为 ωp的探测光照射到能级结构中时,若探测光能够为原子在 |0〉 基态和|1〉激发态之间跃迁提供足够的能量,原子将从|0〉基态跃迁到 |1〉 激发态并吸收几乎全部的探测光,从而得到一个明显的吸收光谱,跃迁路径为:|0〉→|1〉。当在 |2〉亚稳态和 |1〉 激发态之间加入强度为 ωc的泵浦光时,亚稳态和激发态能级跃迁被打通,新的跃迁路径为:|0〉→|1〉→|2〉→|1〉。两种不同的跃迁路径之间产生相消干涉,导致探测光不再被吸收,从而形成一个明显的透明窗口,即电磁诱导透明现象。EIT透射窗口的特性在光学方面也有重要的应用,目前光学耦合谐振腔的EIT效应已经在光子晶体波导[15-17]、平行平板波导[18-19]和表面等离子体[20-24]等很多光学结构中被发现。
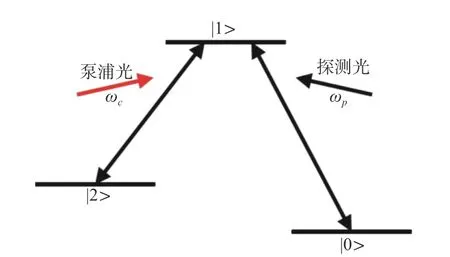
图1 电磁诱导透明三能级模型Fig.1 The three-level model of electromagnetically induced transparency
本文设计的单向波导由正方晶格的钇铁石榴石介质柱(YIG)光子晶体构成,其半径r=0.13a(a为晶格常数),介电常数 ϵ=15。在一对大小相等方向相反的外磁场作用下,该磁性光子晶体结构的时间反演对称性被破坏,并产生一个单向畴壁,使得限制在其中的电磁波呈现单向传输特性[25-26]。单向耦合谐振腔波导结构如图2所示,其中:上半部分和下半部分分别代表方向相反的外加磁场,整个结构的边界条件设置为完美匹配层(PML);H1和H2分别代表两个谐振腔与波导的距离,D表示两个腔之间的水平距离。基于三能级理论,在光子晶体中不同高度挖空两组2*2的介质柱构造两个共振频点不同的高Q值谐振腔,其共振频点分别为 ωA和 ωB。当光源从左边端口输入,在波导中将产生单向的边缘模式。设 φ和 δAB分别为电磁波在两个腔中一个往返产生的相移和衰减,当两个腔满足相位匹配条件φ=2nπ并且 δAB=2τtotal(ωA−ωB)≠0 时(其中τtotal为电磁波在两个腔中一个往返所需的时间),耦合进入共振腔的电磁波将形成F-P谐振并形成驻波模式。此时,由于两个腔模之间的相消干涉,导致出现电磁诱导透明窗口。
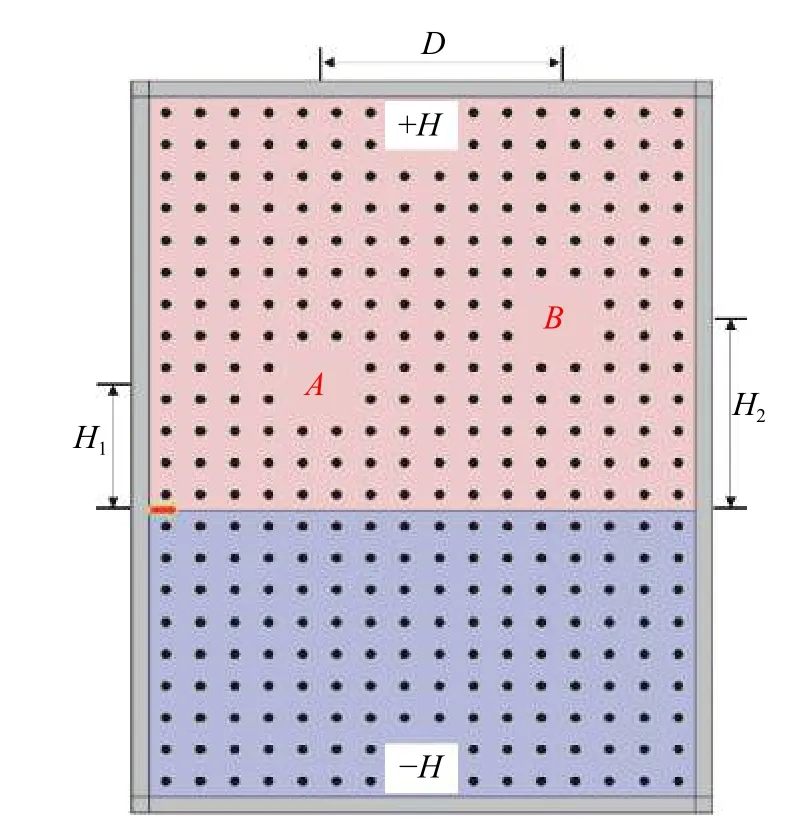
图2 实现EIT效应的耦合谐振腔波导结构Fig.2 Coupled resonant waveguide structure to realize EIT effect
2 仿真结果与分析
采用有限时域差分法对单向电磁诱导透明效应的透射谱进行仿真。图3为光源从左边端口输入时的EIT效应透射谱,此时A、B谐振腔与波导的距离分别为H1=4a、H2=6a。两个谐振腔分别在 ωA= 4.274472GHz和ωB=4.274488GHz处存在各自的共振频点,同时腔A的共振谱明显宽于腔B的透射谱。根据三能级原理,腔A可视为耦合谐振腔波导中的明模腔,腔B可视为暗模腔。当两个谐振腔同时存在时,两个腔的共振谱在 ω=4.27448GHz 附近叠加,并出现了一个向上的透射峰和两个向下的透射谷。由于两个腔模的相互作用,两个透射谷的频点相较单独两个腔的透射谱分别向两个方向发生了偏移。作为对比,当光源从右边端口输入即光反向输入时,由于拓扑波导的单向性,使电磁波无法在波导中传输。
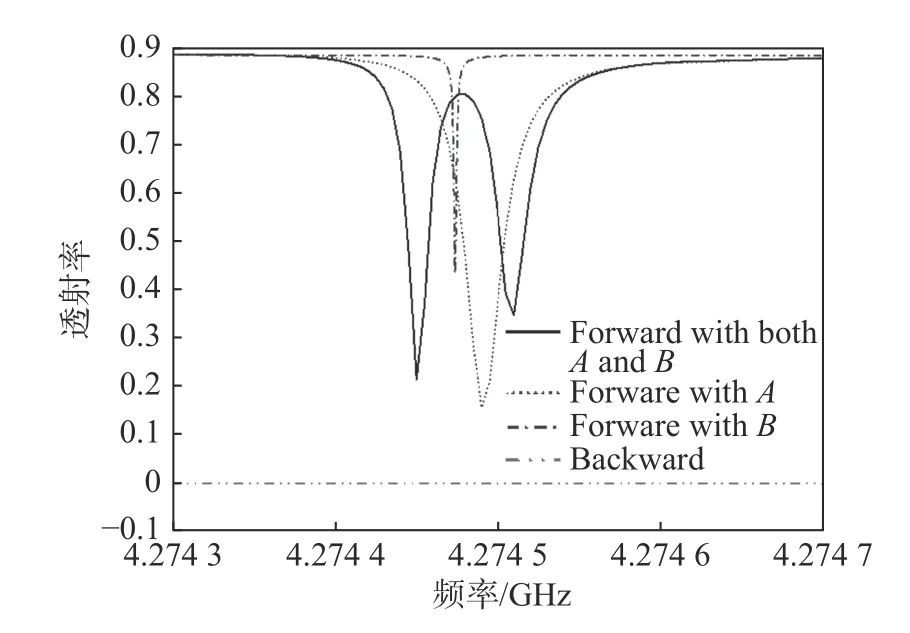
图3 EIT效应透射谱Fig.3 Transmission spectrum of EIT
图4分别给出了两个透射谷和透射峰处z方向的电场分量。当频率为 4.27445GHz 时,两个腔模被同时激发,且能量几乎集中于腔中,如图4(a)所示;当频率位于第二个透射谷4.274 51 GHz时,电场能量同样几乎集中在两个腔内,如图4(c)所示;当频率位于透射峰4.274 48 GHz时,两个腔模同样被激发,但是由于两个腔模之间的相干相消,此时几乎没有能量被局域于腔中,反之,波导中的能量较强,对应的电场分布如图4(b)所示。
为了进一步了解单向EIT效应在拓扑波导中的物理过程与机制,对图4透射谱中每个透射峰(谷)附近的电场分布进行进一步分析。图5分别显示了频率为4.274 44 GHz、4.274 47 GHz、4.274 49 GHz和4.274 55 GHz时的电场分布,其中:图5(a)、(c)和图5(b)、(d)分别为左、右边透射谷两侧频点的电场分布,图5(b)和图5(c)分别为中间透射峰两侧频点的电场分布。由图可知:对于腔A,频点每经过一个透射谷(峰),相应的电场模式均会改变,而腔B内的电场模式只有经过两个透射谷时才会发生模式转换。
通过数值仿真还研究了腔A和腔B之间不同的高度差 ΔH对透射谱的影响。固定腔A的位置不变(H1=4a,D=8a),当ΔH=H2−H1=0时,两个谐振腔的谐振频率相同,此时δAB=2τtotal(ωA−ωB)=0,不能满足EIT效应的条件。ΔH由a增加到3a时:两个腔之间的耦合强度随着距离的增加而减小,代表EIT效应的透射峰和右边的透射谷逐渐发生红移;与之相反,由于决定左边透射谷的共振谱特性主要来源于腔A与波导的相互作用,左边透射谷的偏移量很小,如图6所示。同时,随着 ΔH的增大,代表EIT效应的透射峰逐渐变窄,当 ΔH≥5a时,两个腔之间的相互作用逐渐消失,此时的透射谱对应单个腔A的情况。
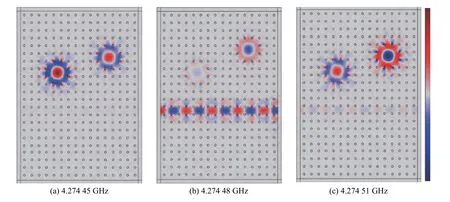
图4 透射峰(谷)处的电场分布Fig.4 The Ez distribution corresponding to the frequency at each transmission peak (dip)
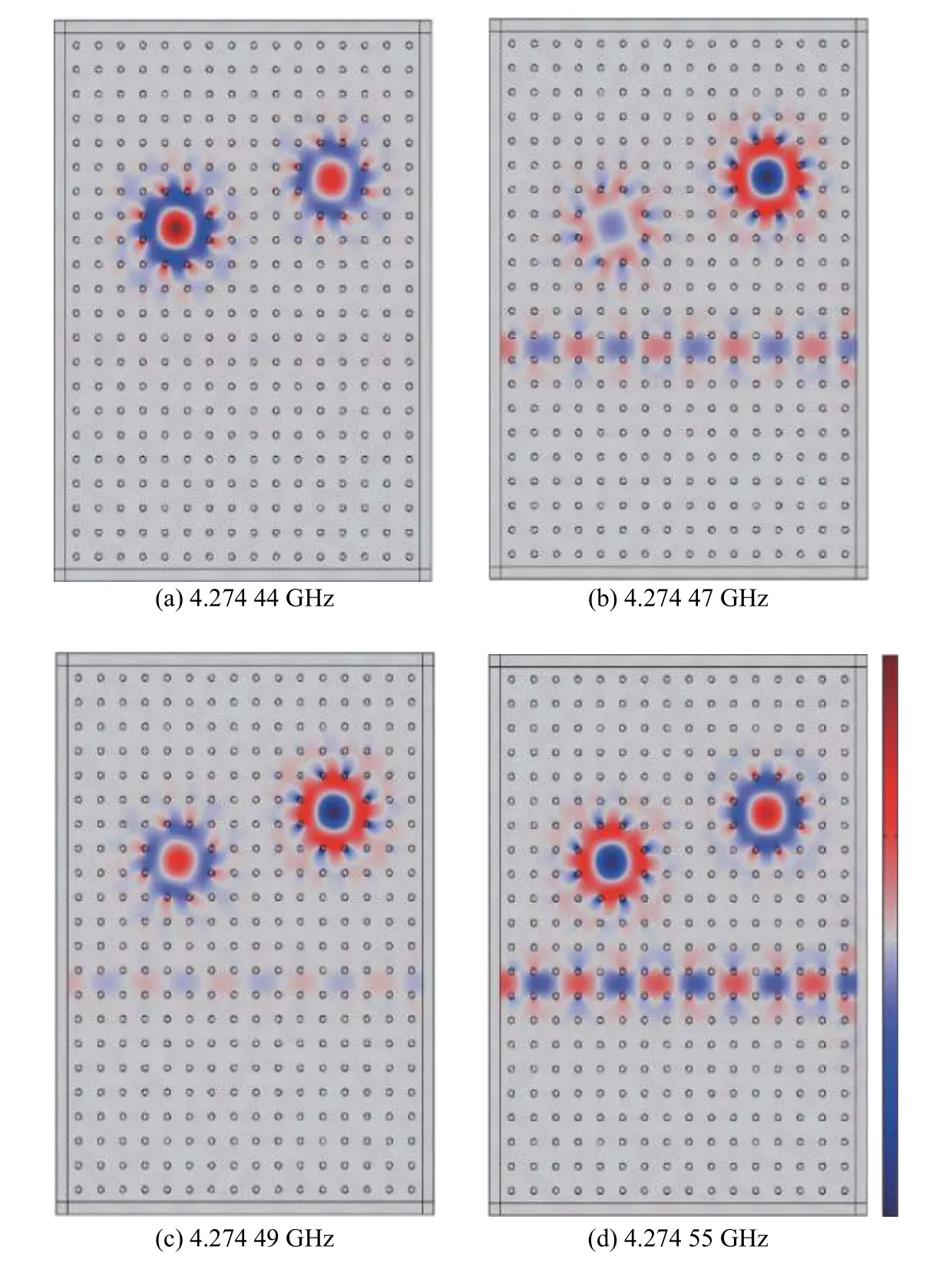
图5 透射峰(谷)两侧频点对应的电场分布Fig.5 The Ez distribution corresponding to the frequency on both sides of each transmission peak (dip)
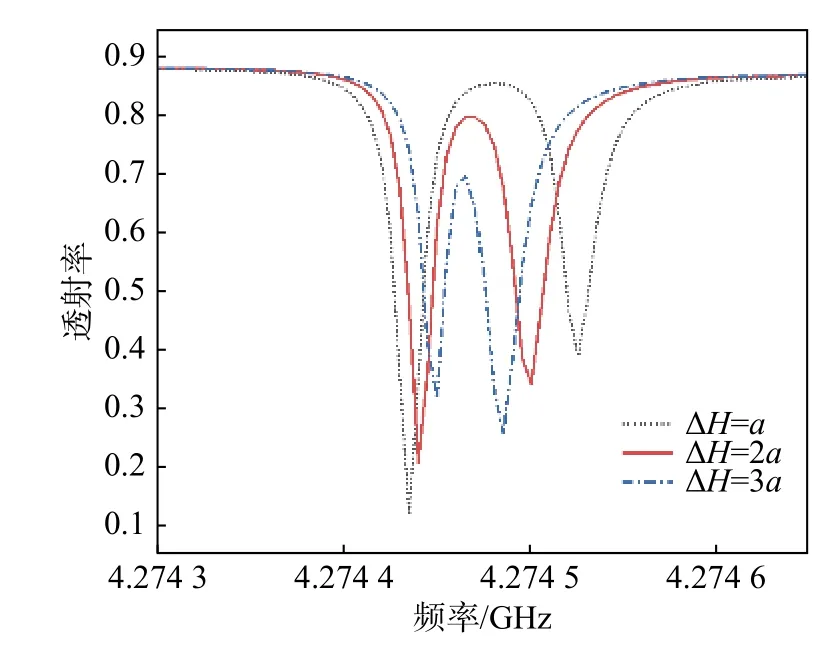
图6 耦合距离对EIT效应的影响Fig.6 The effect of coupling distance on EIT effect
3 结论
通过设计一种基于拓扑单向波导的耦合谐振腔波导结构,实现了具有单向性质的电磁诱导透明效应。通过有限时域仿真得到的透射系数,详细分析了其实现电磁诱导透明的物理机制。此外,通过改变两个谐振腔的耦合距离,研究了电磁诱导透明的频率可调现象,发现随着耦合距离的增加,电磁诱导透明窗口发生红移。
