基于概率统计的电力负荷时间序列预测模型

摘  要： 电力负荷预测属于设置发电计划与电力系统发展的核心，高精度的负荷预测对于电力系统经济、安全、稳定的工作存在着不可忽视的作用。为此，构建基于概率统计的电力负荷时间序列预测模型，采用基于概率主分量分析模型的电力运行数据预处理方法，去除冗余數据。对预处理后的电力运行数据，通过基于多变量时间序列的电力负荷预测模型，实现电力负荷预测。经实验验证，所构建模型对电力负荷的预测结果可信度高，且对短期、长期的电力负荷的预测精度均显著，针对不同时间序列类型的电力负荷预测任务而言，均可实现高精度、全方位的电力负荷预测，可作为电力负荷预测任务中的参考模型。

关键词： 电力负荷预测; 概率统计; 时间序列; 预测模型构建; 数据预处理; 实验验证

中图分类号： TN911.1?34; TU413                  文献标识码： A                    文章编号： 1004?373X（2020）21?0179?04

Power load time series forecasting model based on probability statistics

JIA Qinglan

（College of Mathematics and Statistics， Cangzhou Normal University， Cangzhou 061000， China）

Abstract： Power load forecasting is the core of power generation planning and power system development. High?precision load forecasting plays an important role in the economic， safe and stable work of power system. Therefore， a power load time series prediction model based on probability statistics is constructed， and a power operation data pretreatment method based on probabilistic principal component analysis model is adopted to remove redundant data. For the pre?processed power operation data， the power load prediction model based on multivariable time series is adopted to realize the power load prediction. The result of experimental verification shows that the built model are of high reliability for the power load forecast results， and are significant for short?term and long?term power load forecasting accuracy， can achieve high accuracy and all around power load forecasting for all different types of power load time series forecasting， and can be used as a reference model of power load forecasting task.

Keywords： power load forecasting; probability statistics; time series; forecasting model construction; data preprocessing; experimental verification

0  引  言

近几年，伴随经济的高速发展与生活水平的优化，电能的需求量愈发显著，电能供不应求的情况逐渐加重。所以，高精度的电力负荷预测工作不单可以让未来电网的经济性、合理性、安全性均得到优化，且对设置发电机组的开关与国民经济的发展均存在十分关键的影响[1]。

负荷预测为按照电力负荷历史数据预测未来的负荷，近几年负荷预测方法得到相关学者的重点关注，很多新型理论与方法逐渐出现，对电力负荷均起到了举足轻重的作用[2?3]。但此类方法均是构建于单变量时间序列之上，按照Takens嵌入原理，仅需要嵌入维数与延迟时间选取不存在异常的单变量时间序列能够实现相空间重构，方可获取高精度的预测结果[4]。但实际应用时，电力负荷时间序列存在噪声，所以，在预测阶段，电力负荷预测会遭到噪声干扰，致使时间序列数据出现缺损情况，导致预测精度受损，为此，本文将概率主分量分析模型使用在电力负荷预测里，构建一种基于概率统计的电力负荷时间序列预测模型，以期实现电力负荷的高精度预测[5]。

1  基于概率统计的电力负荷时间序列预测模型

1.1  概率主分量分析模型的电力运行数据预处理方法

电力负荷时间序列预测需要设置概率模型，设置完概率模型后，运算电力运行数据的原始预测变量的概率分布。并且保证原始变量分布于潜藏变量条件下，潜藏变量分布于原始变量中，保证预测变量中不存在冗余数据[6]。

1） 设定电力负荷预测变量的潜藏变量是[S]，使用电力负荷潜藏变量运算获取原始预测变量[Y]的条件分布，然后按照正态分布的有关属性特征运算获取期望[DYS]与条件方差[DPWYS]：

[DYS=DVS+α+βS=VS+α]   （1）

[DPWYS=DVS+α+β-VS-α?VS+α+β-VS-αTS=χ2L]  （2）

式中：[Y]处于潜藏变量[S]的环境分布设成[MVS+α，χ2L];[L]表示单位矩阵;[α]描述均数向量;[β]描述残差项;[V]表示载荷矩阵;[χ]描述概率因子;[D]描述期望因子。

2） 对电力运行数据实施原始预测变量的分布运算，按照原始预测变量的特征和正态分布的属性运算获取变量[Y]的分布，得到[Y]的期望与方差，按照双期望定理能够获取：

[DY=FFYS=α] （3）

[DPWY=DY-αY-αT=VVT+χ2L] （4）

3） 得到电力运行数据原始预测变量[Y]的分布特征后，研究获取潜藏变量[S]的条件分布[FSY]，按照正态分布的属性能够获取：

[FSY=DPWSYTD-1Y-χ] （5）

[DPWSY=L-VTD-1V] （6）

[DPWYST=FY-χST=FVS+χ+α-χSTS=V] （7）

式中[F]表示降维系数。

按照[B+VCW-1=[B-1-B-1VCL+WB-1VC-1?]

[WB-1]]能够获取：

[D-1=χ-2L-χ-2VR-1VT] （8）

式中[W]描述权重。

变量[S]在设定原始预测变量[Y]中的期望是：

[FSY=DPWSYTDPWY-1Y-χ=R-1VTY-α] （9）

式中：[R]描述按照式（8）的数学期望，运算潜藏变量[S]在指定电力负荷原始预测变量[Y]中的条件期望，把原始预测变量的[E]行[E]列矩阵[D]的逆转换为[p]行[p]列矩阵[N]的逆，此方法让预测变量分析的速度大大提高。

[DPWSY=L-VTD-1V=χ2N-1]     （10）

[S]处于原始预测变量[Y]中的条件分布描述成[7?8][MR-1VTY-α，χ2R-1]。

按照上述流程能够完成概率主分量分析模型的建立，能够有效去除电力运行时存在的冗余数据。

1.2  基于多变量时间序列的电力负荷预测模型

基于1.1节预处理后的电力运行数据，将预处理后的电力运行数据中[N]维多变量时间序列设成[Y1，Y2，…，YM]，其中[Yj=y1，j，y2，j，…，yN，j]，如果[N]的值是1，[Yj]描述单变量时间序列，属于多变量时间序列的特例，通过相空间重构方法获取延迟时间重构：

[Um=y1，m，y1，m-δ1，…，y1，m-e1-1δ1，y2，m，y2，m-δ2，…，          y2，m-e2-1δ2，…，yN，m，yN-δN，…，yN，m-eN-1δN] （11）

式中：[m=max1≤j≤Nej-1δj+1，…，M]，第[j]个时间序列的延迟时间与嵌入维数依次设成[δj]，[ej]，[j=]1，2，[…]，[N];将重构相空间相点设成[Wm];时间序列样本数量总值设成[M]。

按照Takens嵌入定理，如果嵌入维数[e]较大，吸引子维数设成[E]，那么具有确定性映射[Ωe]：

[Wm+=ΩeWm]  （12）

或等效模式是：

[y1，m+1=Ω1y1，m，y1，m-δ1，y1，m-e1-1δ1y2，m+1=Ω2y1，m，y1，m-δ1，y1，m-e1-1δ1，y2，m，y2，m-δ2，y2，m-e2-1δ2           ?yN，m+1=ΩNy1，m，y1，m-δ1，y1，m-e1-1δ1，…，yN，m，yN，m-δN，yN，m-eN-1δN]

（13）

式中：[yj，m+1]描述重构相矢量[Wm+1]里第[j]个时间序列的预测值。

所以，如果[Ωe]的确定性函数模式不存在模糊性，即可预测[yj，m+1]。在真实预测中重点关注负荷时间序列的预测，所以，仅分析式（13）里的第一种状况[9?10]，即预测[yj，m+1]。

混沌理论使用在负荷预测的核心就是嵌入维数和延迟时间的选取[11]。由于其和重构空间的近似水平与吸引力值存在较大关联性，所以，延迟时间主要将各维时间序列通过互信息的第一个极小值获取;嵌入维数通过预测误差最低值获取，即符合预测准确率在某个嵌入维中抵达最高值后，会伴随嵌入维数的变大而变小，运算流程如下：

1） 对电力负荷每个时间序列实施归一化操作。

2） 使用互信息法获取电力负荷每个时间序列的延迟时间[δj]，同时设置嵌入维数[ej]的取值区间，[j=1，2，…，N]。

3） 针对获取的嵌入维数实施相空间重构，使用欧氏距离判断电力负荷预测中心点[Wm]的最近邻域点[Wi]：

[Wi=minWm-Wj，    j=max1≤j≤Nej-1δj+1，…，M，                   m=max1≤j≤Nej-1δj+1，…，N                            （14）]

4） 将[Wi]的后续演化点的首个分量[y1，i+1]设成[y1，m+1]的预测值，同时运算平均1步绝对预测误差[Ge1，e2，…，eN]：

[Ge1，e2，…，eN=1M-t+1i=tMy1，m+1-y1，m+1，]

[t=max1≤j≤Nej-1δj+1] （15）

式中：[t]表示时刻;[M]描述步数;真实值与预测值依次设成[yj，m+1]，[y1，m+1]。

5） 提高嵌入维数[ej]，多次执行步骤3）、步骤4），当全部嵌入维数循环完成再停止[12]。

6） 围绕嵌入维数[ej]的差异取值，设置最小的平均1步绝对预测误差相应的最佳嵌入维数[e10，e20，…，eN0][13?15]为：

[e10，e20，…，eN0=minGe1，e2，…，eNe1，e2，…，eN，j=1Nej≠0] （16）

最佳嵌入维数设成最低预测误差是因为如果嵌入维数较小，非合理的嵌入会让吸引子重复出现在某处，便会存在交接情况，因此在交接范围的邻域里存在吸引子差异部分的点，所以此时的预测精度低;如果嵌入维数变大至最佳嵌入维数时，合理的嵌入与映射可以提升预测精度，但离预测状态不近的电力运行历史数据对预测干扰不大，同时噪声对预测精度的干扰变大，致使预测精度变高。所以，将预测误差等于最低值时的嵌入维数设成最佳嵌入维数。

2  仿真实验

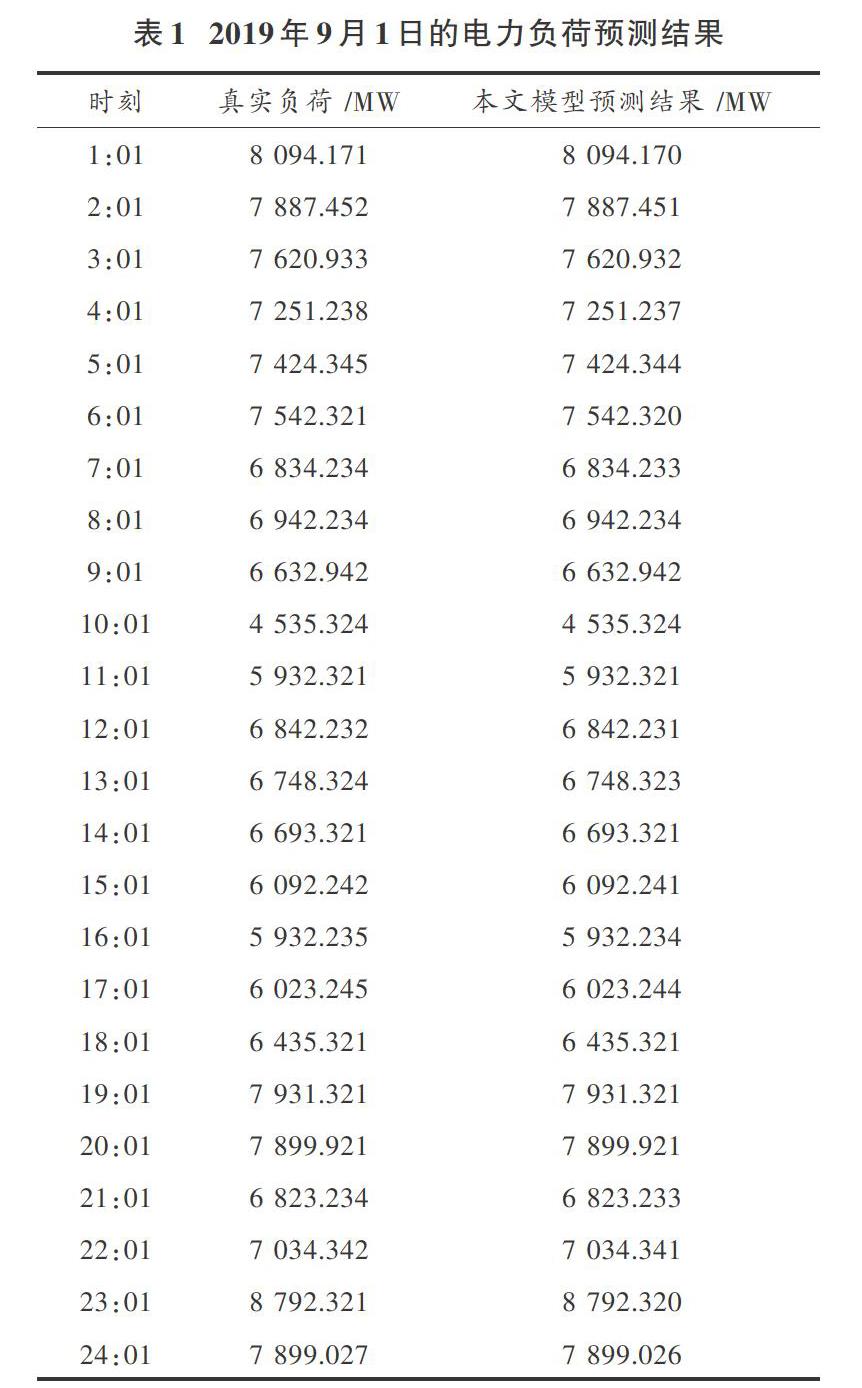
为了测试本文模型的有效性，使用本文模型预测辽宁省沈阳市某小区2019年1月—9月的电力负荷数据，将7月—8月的电力负荷数据设成训练数据，对2019年9月负荷实施预测，9月1日的电力负荷预测结果见表1。由表1可知，本文模型预测误差最大值仅有0.1%，误差极低，由此验证本文模型对电力负荷的预测存在可信性。

上述实验是本文模型对电力负荷的短时间预测，为分析本文模型的应用性能，采用本文模型对该小区2019年1月—9月的电力负荷数据进行中期预测，并依次采用适应性子集度神经网络的电力负荷时间序列预测模型、基于改进回归法的电力负荷预测模型实施预测后与本文模型的预测误差进行对比，结果见表2。分析表2可知，本文模型对该小区2019年2月—9月的电力负荷数据实施中期预测后，预测误差均值为0.1%，适应性子集度神经网络的电力负荷时间序列预测模型、基于改进回归法的电力负荷预测模型的预测误差高出本文模型数倍，经验证，本文模型对电力负荷的中期预测存在显著优势。

因为电力负荷和用户用电的时间序列存在直接联系，为此，为测试本文模型的使用优势，对电力运行数据中导进噪声数据，并从一般休息日、重大节假日两个角度测试三种模型的预测精度，结果依次如图1、图2所示。分析图1，图2可知：在普通休息日与重大节假日中，本文模型对电力负荷的预测精度均高达0.99;适应性子集度神经网络的电力负荷时间序列预测模型对电力负荷的预测精度最大值依次是0.87，0.93;基于改进回归法的电力负荷预测模型对电力负荷的预测精度最大值依次是0.81，0.88。由此可见，虽然电力运行数据中存在噪声数据，但本文模型对一般休息日、重大节假日的电力负荷预测精度未受影响，预测精度较高，而另外两种模型的抗干扰性能差，预测精度低。

使用三种模型对该小区2009年—2019年的电力负荷实施预测，以此测试三种模型对电力负荷的长期预测精度，结果见表3。根据表3中数据显示，本文模型对该小区2009年—2019年的电力负荷实施预测后，预测精度高于98%，适应性子集度神经网络的电力负荷时间序列预测模型、基于改进回归法的电力负荷预测模型的预测精度低于90%，差异显著。

测试三种模型对短期、中期、长期的电力负荷预测时对电力运行数据的漏测率，依次测试三种模型是否可以全面预测电力负荷情况，结果如图3所示。由图3可知，本文模型对电力负荷的短期、中期以及长期预测时，漏测率均低于对比模型，预测范围全面。

3  结  论

本文构建了一种基于概率统计的电力负荷时间序列预测模型，并通过实验验证了其有效性，且在实验中对其预测性能实施多方位测试，测试后可知：

1） 本文模型对短期电力负荷的预测误差最大值仅有0.1%，误差极低。

2） 本文模型对中期电力负荷数据实施预测后，预测误差均值为0.1%。

3） 在普通休息日与重大节假日中，本文模型对电力负荷的预测精度均高达0.99。

4） 本文模型对长期电力负荷实施预测后，预测精度高于98%。

5） 本文模型对电力负荷的短期、中期以及长期预测时，漏测率均低于对比模型。

参考文献

[1] 杨斌，杨世海，曹晓冬，等.基于EMD?QRF的用户负荷概率密度预测[J].电力系统保护与控制，2019，47（16）：1?7.

[2] 蒋玮，黄丽丽，祁晖，等.基于分布式图计算的台区负荷预测技术研究[J].中国电机工程学报，2018，38（12）：3419?3430.

[3] 张昊，焦克莹.基于多元逆模糊数的模糊时间序列预测方法[J].数学的实践与认识，2019，49（9）：147?151.

[4] 孙若莹，范厚明，赵刚.基于强化学习的非线性时间序列智能预测模型[J].大连海事大学学报，2017，43（4）：97?103.

[5] 蔡林芝，吕王勇.基于Tukey法改进时间序列平稳性检验的分段检验法[J].统计与决策，2018，34（16）：26?29.

[6] 董子晗.基于混沌时间序列的地区电网负荷预测[J].电网与清洁能源，2019，35（5）：38?41.

[7] 赵兵，王增平，纪维佳，等.基于注意力机制的CNN?GRU短期电力负荷预测方法[J].电网技术，2019，43（12）：4370?4376.

[8] 李永通，陶顺，赵蕾，等.基于短时间尺度相关性聚类的负荷预测[J].电测与仪表，2019，56（16）：32?38.

[9] 王岩，孔林，李艺丰，等.微电网需求响应策略的连续时间序列仿真[J].电力系统及其自动化学报，2019，31（10）：52?58.

[10] 张健萍，周东.基于概率统计的土石混合体边坡可靠度分析方法[J].中国安全科学学报，2018，28（5）：141?146.

[11] 张淑清，刘子玥，何泓运，等.基于多变量加权一阶局域混沌预测模型优化及应用[J].计量学报，2018，39（1）：77?82.

[12] 周任军，石亮缘，汤吉鸿，等.多功率曲线协整度约束下的源?荷?储优化协整模型[J].中国电机工程学报，2019，39（12）：3454?3464.

[13] 高昆仑，杨帅，刘思言，等.基于一维卷积神经网络的电力系统暂态稳定评估[J].电力系统自动化，2019，43（12）：18?26.

[14] 黄越辉，曲凯，李驰，等.基于K?means MCMC算法的中长期风电时间序列建模方法研究[J].电网技术，2019，43（7）：2469?2476.

[15] 薛阳，王琳，王舒，等.一种结合CNN和GRU网络的超短期风电预测模型[J].可再生能源，2019，37（3）：456?462.

作者简介：贾庆兰（1978—），女，河北沧州人，硕士，讲师，研究方向为数学概率统计。