基于以学生为中心的大学数学类课程教学改革七步法探究与实践
2020-12-07程红萍
程红萍

[摘 要]大学数学类课程有着概念难理解、知识点多、逻辑性强的特点,基于此,文章结合当前大学类数学课程教学的现状,围绕以学生为中心的教学理念对大学数学类课程教学改革七步法进行了探究与实践,以期能有助于提高学生的通识能力,同时又能达到高效教学的目的。
[关键词]以学生为中心 大学数学类课程 七步法
基金項目:教育部2018年粤嵌科技产学合作协同育人项目(项目编号:201802153104);西安欧亚学院重点课程建设基金项目(项目编号:2018KC032)。
中图分类号:[G640] 文献标识码:A
大学数学类课程具有概念难理解、知识点多、逻辑性强的特点,这导致许多学生害怕学习大学数学类课程。为了帮助学生克服学习大学数学类课程的畏难情绪,更好地激发学生学习大学数学类课程的热情,许多专家、学者对大学数学类课程教学改革作了大量的研究,如温立书等将一体化教学模式引入大学数学课堂,目的是提升学生的综合能力;王发兴等给出多媒体在大学数学建设和使用过程中的七步法建议,目的是提高大学数学类课程教学效果;徐东胜等在大学数学类课程教学方法上给出数学类基础课的“考一考、说一说、讲一讲、做一做、想一想”五步法改革,目的是调动学生的学习自觉性……以上这些研究基本上都是基于某一方面来进行的大学数学类课程教学改革探索,而大学数学类课程是属于大学通识教育的一门公共基础课程,其教学目标是培养学生的批判性思维能力、创新思维能力、团队协作能力、解决问题能力、自主学习能力等,这也是通识教育的特点所在,因而大学数学类课程教学改革也应该结合这些特点来进行相应的探索与实践。笔者在多年教授大学数学类课程的基础上,且经过自身的不断实践、探索、反思和改进,并且结合通识教育的相关特点,围绕着以学生为中心的教学理念对大学数学类课程教学改革“七步法”进行了深入的探究与实践。
大学数学类课程教学的现状
1.教学目标单一
目前大学数学类课程教学目标大多局限于学生对各章节知识体系及知识点的掌握程度上,很少涉及学生数学素养和通识能力方面的提升。
2.教学方法单一
大学数学类课程教学主要是以理论知识讲授为主的,实践环节设置极少或者根本没有相应的实践环节。大多数教师在课堂上主要是以黑板或PPT显示为主来讲授相关的数学理论知识,这种单一的授课方式很难激发起学生的学习兴趣。
3.课堂上师生、生生互动方式单一
课堂的大部分时间仍然是教师在唱“独角戏”,课堂师生的互动方式主要是教师提问、学生回答,而多元化的讨论式、交流沟通式、小组合作式的课堂互动方式几乎没有,这种单一的师生、生生互动方式是很难产生高效且有深度的课堂学习效果的。
4.课程设计单一
课程设计基本上只考虑教师的教法,很少涉及学生的学法。在学习目标方面往往也只是列出一般性目标,很少列出具体的目标。这种简单的课程设计很难培养出学生的自主学习能力。
5.考核评价学生的标准单一
目前考核评价学生的基本方式是“平时成绩+期中考试成绩+期末闭卷考试成绩”。学生为了考到相应的合格分数,往往采用被动的学习方式应付考试,这种传统的考核评价方式无法更好地提高和展现学生的综合能力。
大学数学类课程教学改革七步法
不论是经济类数学课程,还是工科类数学课程,其教学目标都是培养学生的通识能力。通过对大学数学类课程教学现状和存在问题的分析来看,对学生通识能力的培养力度还是不够的。笔者在多年的不断实践、探索、反思和改进中发现:教学中我们应该以学生及学生的学习效果为中心,以发现学生的学习困难所在和促进学生有效学习为目的,然后以学生调查分析、课程认知框架、要解决的问题、课程设计、设计理由、考查内容、评价标准为主的大学数学类课程改革七步法来推进大学数学类课程教学改革,如图1所示。
1.学生调查分析
首先是制作调查问卷,问卷内容主要包括基本情况(如高考成绩、学生对数学难度的评价)、知识方面、应用方面(如学习数学对自身专业的帮助、对提升自身观察能力的帮助)学习方法四大部分。
其次是发放问卷、收集问卷和分析问卷。本次我们对欧亚学院2018级1300名学生进行了问卷调查,共收回有效问卷1292份,其中学习经济数学课程的学生占比68%,学习工科数学课程的学生占比32%;与此同时还访谈了75名学生,其中商科(经济类学生)40名,工科(工科类学生)35名。得到的结论是:92%的学生高考成绩普遍分布在81~100分之间;61%的学生认为学习大学数学类课程难度比较大;36%的学生对大学数学类课程的喜爱程度一般;62%的学生课外学习方法普遍是题海战术和讨论学习;81%的学生每天课下学习时间平均为1~2小时;53%的学生一学期中与教师沟通的次数平均为1~2次;67%的学生与教师交流的方式主要是面对面交流;76%的学生在学习中遇到困难往往选择寻找网络资源或与同学讨论;56%的学生在完成作业的过程中与同学合作完成的次数大约在5~10次;68.4%的学生认为学习方法对自己学习很重要;69%的学生大学阶段的数学学习方法是网络辅导和讨论式学习;67%的学生有时候会对知识点进行总结,58%的学生认为数学对解决日常问题的帮助程度一般;48%的学生认为大学数学类课程对自身的专业能力提升非常有帮助,52%的学生认为数学计算对提升自身分析能力非常有帮助;94%的学生认为作业量适中;53%的学生认为数学中的概念等在大学数学类课程中是十分重要的。
2.课程认知框架
以工科认证中的通信专业对工科数学课程的要求为例,从毕业要求、指标点、课程目标三个维度来制定规范的大纲。如课程目标要体现毕业要求,还要与课程内容、教学方法合理衔接。在此基础上对每一章节进行仔细梳理,然后制作出知识框架图,框架图中要明确标注相应的知识点。
3.要解决的问题
我们要通过对学生调查分析和对课程认知框架的梳理找准要解决的问题。如大部分学生基础比较薄弱、学习数学知识的过程遇到的困难多;学习过程中没有成就感;数学课程与其专业的结合度不高,对自己分析和解决问题能力的提升所起的作用一般;超过半数的学生能够认识到总结和反思的重要性,但在實际操作过程中并没有完全做到及时总结和反思……通过我们课程组的多次讨论和协商,最后我们的应对策略是:一是要善于将大学数学类课程中的难点内容转化为学生容易理解的内容;二是要巧妙地将学生生活中的认知经验迁移到学生大学数学类课程的学习之中,激发学生探究知识的热情;三是要在教学过程中发现学生的错误并要及时纠正,促使学生在学习中形成持续的学习动力;四是要在大学数学类课程教学中加大专业背景的案例教学、渗透科研项目及数学模型的案例分析和应用;五是要引导学生及时总结和建立各知识点之间的联系和知识框架图,还可以建立辅导答疑咨询工作坊,甚至可以联合学生处、教务处,在每周二和周五20∶00到22∶00安排相应的教师在学生第一社区对学生进行大学数学类课程的辅导答疑。
4.课程设计
笔者和经济类数学课程组、工科类数学课程组的教师在反复讨论、学习、借鉴及实践的基础上,依托课程矩阵从一般性目标(知识内容与课程目标要求)、具体目标(知识点细化、分解一般性目标)、教师教法(教师角色转变:组织、引导、帮助和脚手架;选取合适的教学方法:讲练结合法、混合式教学)、学生学法(可以自学的一律不教;文理分组、同伴学习、学习提纲)、效果评价(测试题分层、问题具有开放性、兼顾通识能力培养)五个方面对数学类课程进行了相应的设计。
5.设计理由
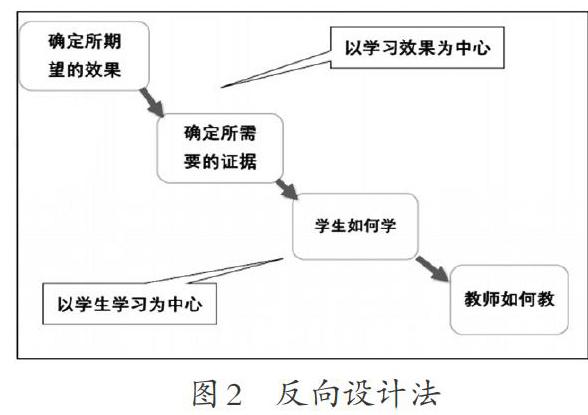
课程设计时遵循布鲁姆的目标分类理论认知领域及布鲁姆学习能力金字塔原则,从而得出学生对学习内容的平均留存率:教授给他人90%,实践75%,讨论50%,演示30%,视听20%,阅读10%,听讲5%。因此,以学生和学生学习效果为中心,采用反向设计法。具体如图2所示。
6.考查内容
考查内容主要从学习效果、知识内容、能力增量方面来进行。对学习效果分为过程性考查(过程性目标)和终结性考查(认知性目标);知识内容分为概念性知识、程序性知识、元认性知识。
7.评价标准
评价标准分为过程评价、终结评价、效果评价。过程评价包括课堂表现、小组活动评价、章节小测验评价、作业评价,终结评价包括考试评价、项目评价,效果评价包括教师自评、学生自评、管理评价。每一部分都制定相应的评价标准以保证评价的合理性和准确性。
结 语
大学数学类课程教学改革七步法改变了以往教学中过于关注数学知识体系而忽视课程与学校发展定位及与学生发展需要相结合的问题,它从社会对人才的需求出发,依据学校的发展定位,以学生和学生的学习效果为中心,立足于学生通识能力和数学素养的提升,重新建立大学数学类课程教学目标。并且在2019级大商科和工科类部分学生的教学实践发现,大学数学类课程教学改革七步法能使学生比较系统地掌握数学基础知识;学生还可以通过大学数学类课程教学改革七步法掌握数学的基本运算与技能,并能对运算结果进行分析、归纳和类比,在分析问题的过程中训练了学生的批判性思维能力;通过项目式教学实践,提高了学生分析问题和解决实际问题的能力;通过数学建模教学及竞赛,可以看出学生能够自觉地运用所学知识建立数学模型,以解决生活或现实社会中的一些数学问题,特别是在数学建模竞赛中,提高了学生的创新思维能力、团队协作能力、自主学习能力,这些都为学生形成正确的价值观打下了坚实的基础。大学数学类课程教学改革七步法的教学工作流程不是一个线性的过程,而是一个反复和迭代的过程,是一个不断完善的过程,在今后的教学实践中还需要我们不断改进。
参考文献:
[1]温立书,王雪茹.基于一体化的高校数学类课程改革[J].教育教学论坛,2018(2):80-81.
[2]王发兴,王志军.大学数学多媒体课件建设应用七步法[J].中国教育技术装备,2014(10):66-67.
[3]徐东胜,黄文,何志雄.大数据背景下数学类基础课程教学改革探索[J].管理观察,2019(8):137-140.
[4]汪泽焱,姚佳.高等数学SPOC混合式教学模式的实践与思考[J].大学数学,2017(1):91-95.
[5]罗晓丽.SPOC在高职院校高等数学教学中的应用[J].考试周刊,2018(25):96.
[6]石玲.SPOC模式在高校教学中的应用——以工程图学课程为例[J].黑龙江高教研究,2016(11):164-166.
作者单位:西安欧亚学院通识教育学院 陕西西安
