基于改进证据理论与IFAHP的预应力砼梁桥状态评估*
2020-12-07张征昀彭步新王子健阳逸鸣
张征昀, 彭步新, 王子健, 阳逸鸣
(1.长沙理工大学 土木工程学院, 湖南 长沙 410114;2.安福县房产管理局, 江西 安福 343206)
桥梁技术状况现行主要评定标准为《公路桥梁技术状况评定标准》。在运用该评定标准进行桥梁结构服役状态评定时,需记录桥梁结构已有病害和各构件的缺陷位置与具体情况,然后按规范中的计算公式和评分标准进行评定。学者门也对桥梁性能评价体系及计算方法进行了研究,如黄侨等基于不确定层次分析法对斜拉桥进行综合服役状态评估,得出影响桥梁安全性和耐久性的主要因素;刘芳平等运用模糊可拓层次分析法对在役桥梁进行评价,所得结果相较于传统层次分析法的评价结果更可靠;熊仲明等以大跨度钢结构为背景建立模糊综合评价模型,提出了大跨钢结构各指标权重向量判断矩阵和钢结构构件鉴定各子指标向量判断矩阵,为大跨钢结构评估结果的准确性提供保障。上述方法虽然具有各自的优势,但难以处理多源信息间的不确定性因素。D-S证据理论是处理不确定性因素行之有效的工具,但针对高冲突证据进行融合所得结果可能与实际情况相反。为此,将改进模糊层次分析法(IFAHP)与改进D-S证据理论相结合,对预应力砼梁桥的技术状况进行评价。
1 IFAHP模糊判断矩阵的权重确定
IFAHP法不仅符合专家的逻辑思维,而且构造形式简单,相较于传统层次分析法更适合对多目标决策问题进行分析。该方法可将初始判断矩阵转换为模糊判断矩阵,减少迭代次数;还能避免传统层次分析法繁琐的一致性检验过程,提高权重计算精度。IFAHP法权重计算步骤如下:
(1) 依据评价对象的层次结构建立优先判断矩阵A=[aij]n×n,用于描述各因素间相对重要程度。其中A为模糊互补矩阵,aij为矩阵中两两因素比较的重要性标度,其值为0.1~0.9,其意义见表1。

表1 模糊判断矩阵标度尺
(2) 对模糊判断矩阵A按列求和,得到ri与rj(i,j=1,2,…,n),然后按rij=0.5(ri-rj+1)将初始矩阵A=[aij]n×n转换为一致性模糊判断矩阵R=(rij)n×n。
(3) 按eij=rij/rji将一致性模糊判断矩阵R=(rij)n×n转换为互反型判断矩阵E=[eij]n×n。
(4) 为使权重向量具有较高的精度并确保证据融合的计算结果合理,采用方根法按下式计算初始排序向量:
(1)
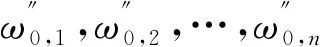

(2)
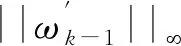
(3)
式中:η为预定迭代精度。
(4)
2 改进的证据理论
D-S证据理论中,定义识别框架Θ={A1,A2,…,An}(n为命题个数),各证据的基本概率赋值函数(BPAF)为mi(Aj),表示证据mi对命题Ai的信任度,合成公式为:
(5)
(6)
式中:K为冲突权值,反映证据之间的冲突程度。
K的取值区间为[0,1],其值越大,证据冲突越大。D-S证据理论在K=1时不再适用,此时证据间完全冲突。为减小冲突证据对评价结果的影响,对引起冲突的证据进行修正。
辨识框架中Rn维空间的坐标使用每个证据的基本概率函数赋值,可将每个证据转化为该空间内的一组向量mi=(mi(A1),mi(A2),…mi(An))T。由于证据源中各证据之间的赋值大小顺序可能产生自冲突性质,基于余弦相似度,采用文献[9]中方法对证据相似度进行重新定义:
Simij=αcos(mi,mj)+βSimseq(mi,mj)
(7)
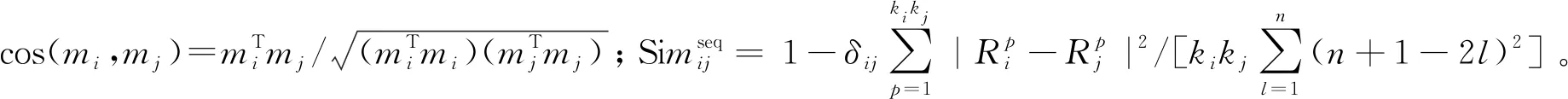
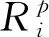
(8)
冲突证据判别因子(运用K近邻法)为:
(9)
该冲突因子的取值区间为[0,1]。Confi=0,表示证据mi与其他证据不存在冲突;Confi=1,表示证据mi与其余证据高度冲突。利用Confi可判断证据间的冲突性,若Confi>τ(τ为判别阈值),则判定mi为冲突证据。
根据式(8)可得出证据mi的信任度为:
(10)
根据式(10)可确定证据mi的相似度,对判别出的冲突证据进行修正后,得到基本概率赋值:
(11)
在修正后的冲突证据中,不确定性命题Θ提供的不确定性信息将增加,信任度小的命题Ak提供的确定性信息将减少,从而降低信任度较小证据带来的影响。
对证据向量mi中原始证据mi(Aj)按式(12)进行修正。
(12)
3 预应力砼梁桥状态评价
3.1 评价模型及评定标准
如图1所示,评价模型的目标层为预应力砼桥梁服役状态,准则层包括主梁、墩台及基础、支座及其他、桥面,指标层包括抗弯可靠度、墩台及基础变位、普通钢筋锈蚀等13项。
根据《公路桥涵养护规范》,将桥梁技术状况评定等级分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ 5类,得评语等级模糊集H={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ},分别表示良好、较好、较差、很差、危险,评价体系中的定性指标依此进行评价。依据相关规范及评定标准,对其中分级指标依照模糊划分原则进行处理,得定量指标评定标准区间值见表2。
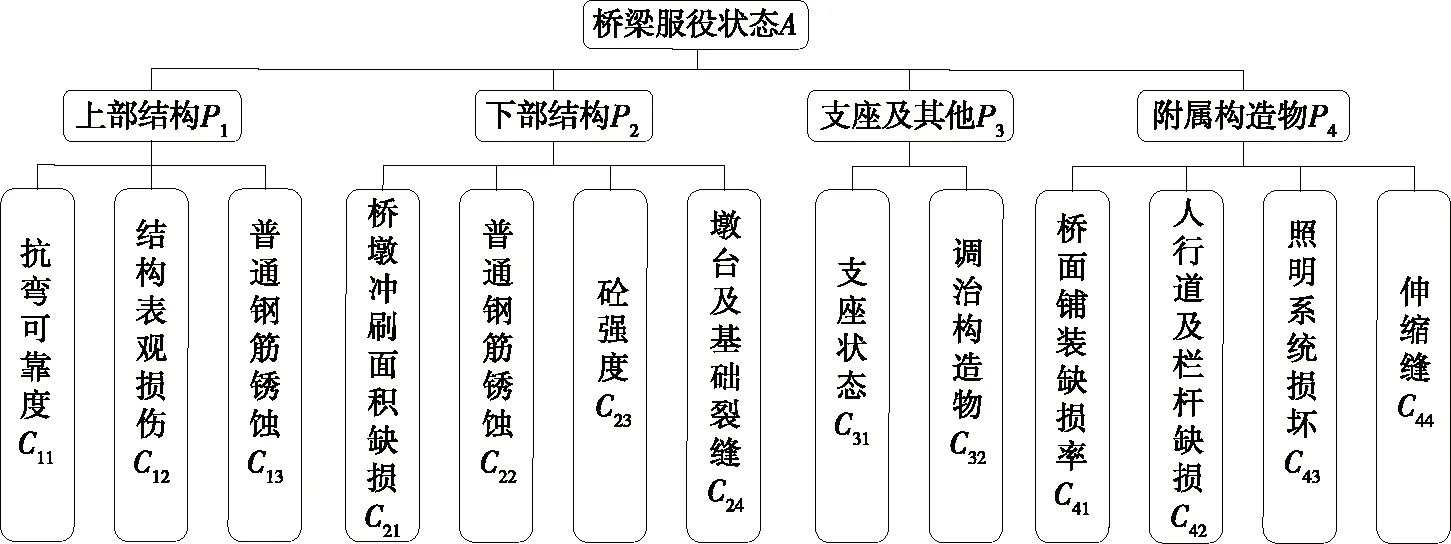
图1 预应力砼桥梁评价模型

表2 桥梁定量指标评定标准区间值
3.2 实测数据
以某高速公路连续梁桥为例,对其进行服役状态评价。该桥于2001年建成通车,为65 m+120 m+65 m三跨预应力砼连续刚构箱梁桥,采用悬臂拼装法施工。由于施工中出现了施工质量等问题,造成桥梁主梁表观出现大量裂缝,且墩台基础和桥面出现不同程度病害,遂于2017年秋对全桥进行检测。检测结果和桥梁可靠指标计算结果见表3。
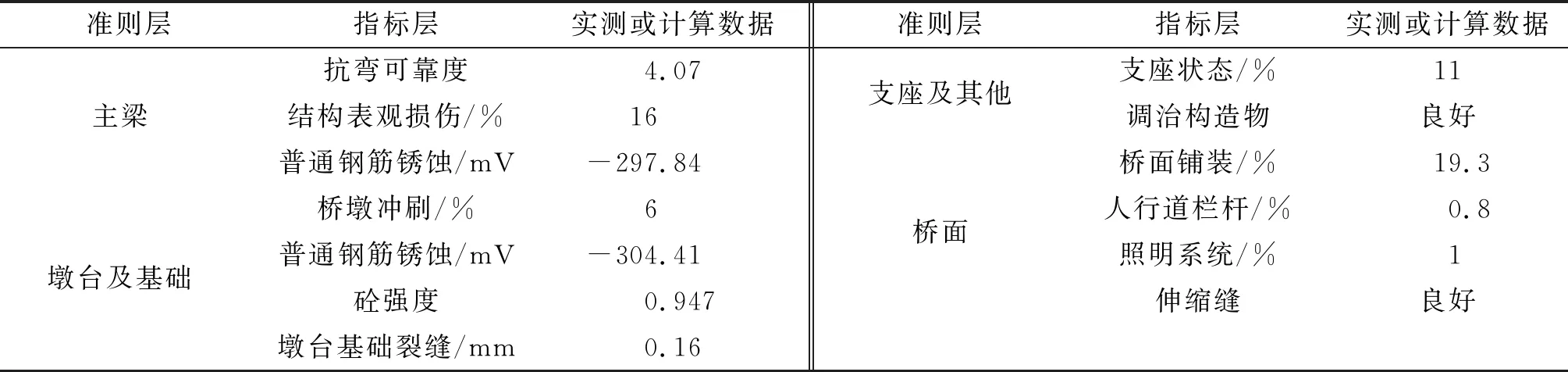
表3 预应力砼桥梁检测数据和可靠指标
3.3 评估过程
3.3.1 构造模型的隶属度函数
为计算简便且尽可能反映各指标的模糊程度,采取梯形建立评估模型的隶属度函数。对于越大越优的评价指标,隶属于Ⅰ级的隶属度函数为:
I1=
(13)
隶属于Ⅱ、Ⅲ、Ⅳ的隶属度函数为:
Ik=
(14)
隶属于Ⅴ级的隶属度函数为:
I5=
(15)
式中:Hk(k=1,2,3,4,5)表示相应评估等级的区间值。
对于越小越优的指标,则将上述隶属函数中max与min、<(≤)和>(≥)进行两两互换。
3.3.2 建立模糊优先判断矩阵
结合评价模型和表1对评价指标进行相对重要性比较,得到桥梁服役状态评价体系中各层模糊判断矩阵。A-P模糊判断矩阵为:

P1-C模糊判断矩阵为:

P2-C模糊判断矩阵为:

P3-C模糊判断矩阵为:

P4-C模糊判断矩阵为:

依据IFAHP法计算得到各指标权重,并通过建立的隶属度函数确定评价等级分布(见表4和表5)。然后将隶属度值与指标权重相乘,得到证据理论中基本概率赋值函数(见表6)。

表4 各指标权重值计算结果
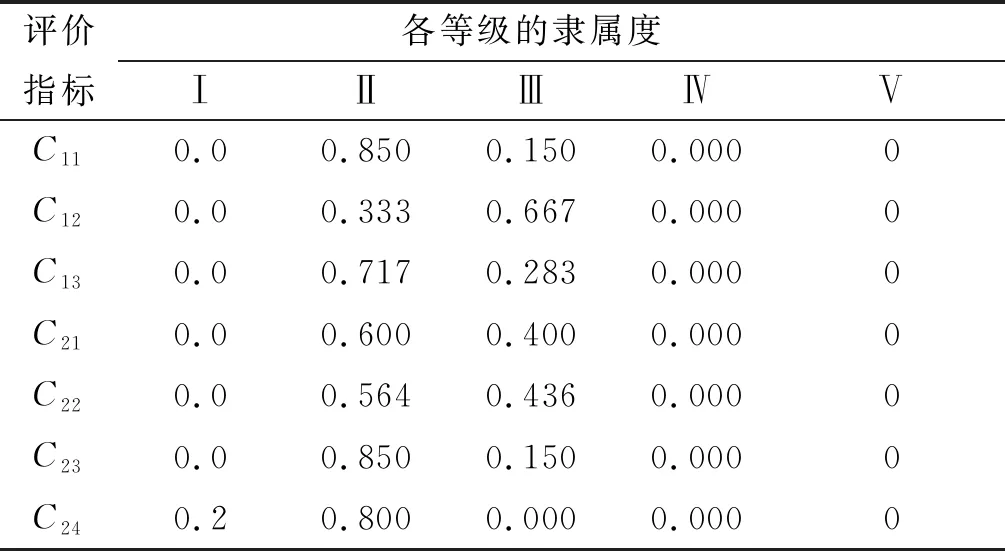
表5 评价指标隶属度分布
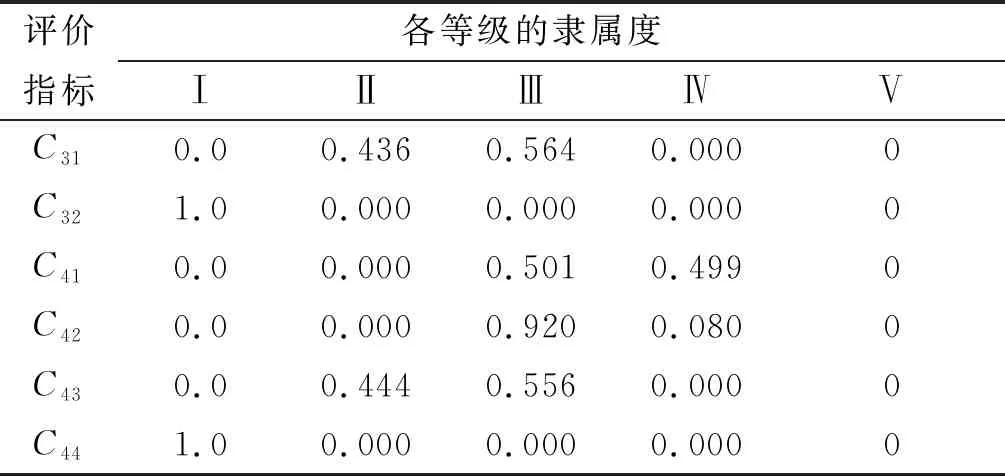
续表5
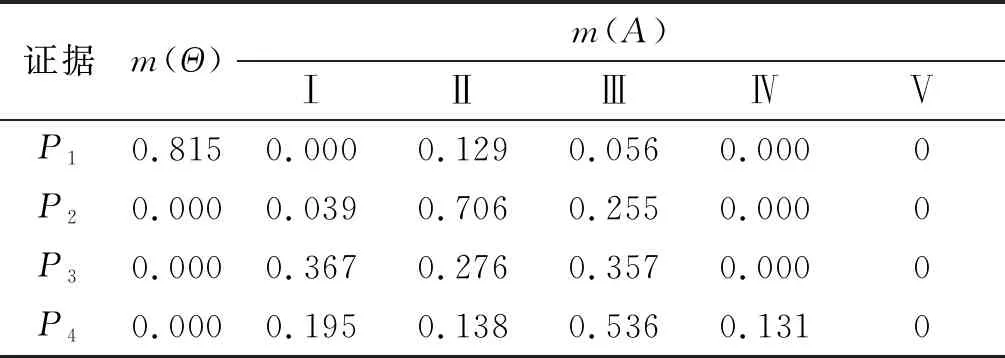
表6 基本概率赋值函数
3.3.3 结果分析
基于同样的基本概率赋值函数,将改进证据理论所得计算结果与模糊综合评判法和未改进的证据理论的结果进行比较,结果见表7。
依照最大隶属度评价准则,模糊综合评判法和未改进的证据理论所得评估结果均指向Ⅱ类桥,而改进D-S证据理论的评价结果指向Ⅲ类桥,为较差的服役状态,需进行加固。
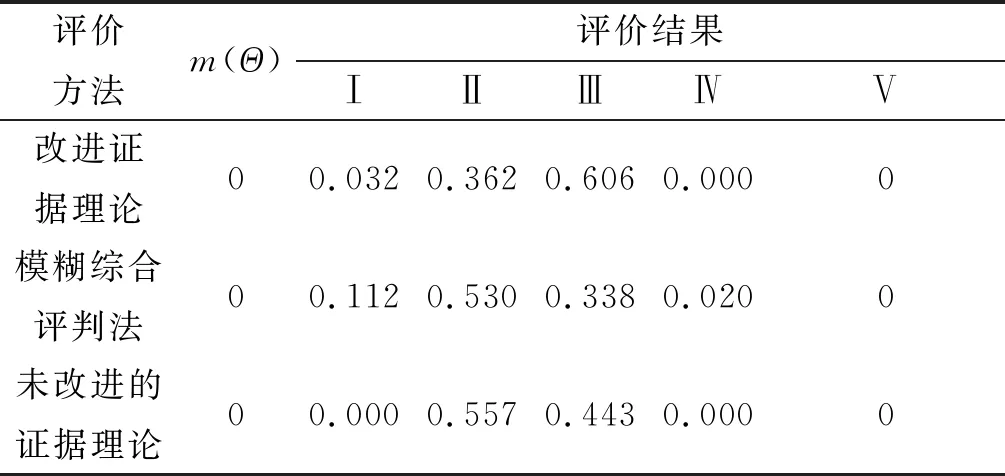
表7 改进证据理论与其他评价方法计算结果比较
4 结语
采用改进D-S证据理论能充分考虑证据间的冲突特性,对高冲突证据进行修正,相较于D-S证据理论,能更有效减少异常证据对评价结果的影响,提升评价结果的可信性。该改进算法能对大跨预应力砼桥梁的服役状态评估提供较合理的解决方法,在桥梁检测评定中有着较广泛的应用前景。
