碳纤维增强复合材料沉头螺栓连接失效分析

王 强,贾普荣,张 龙,王 刚,曾磊磊

（西北工业大学力学与土木建筑学院，西安710072）

复合材料因其比刚度高、比强度高、耐疲劳等优异的力学性能，在飞行器承载结构中得到了广泛的应用。由于设计、制造、成本以及维护等方面的制约，飞行器结构中缺少不了一些工艺分离面、维护口盖和多种外挂接口等[1]，因而结构件间的连接在飞行器中必不可少。螺栓连接因其承载能力强、连接可靠性高、便于安装和拆卸等优点，被广泛用于飞行器结构当中；但由于复合材料是各向异性材料，其损伤和破坏模式特别复杂，即使在单轴拉伸作用下，也会有多种损伤状态同时产生，而在复杂的连接区域，其应力集中状况会比金属结构更为严重，尤其是对于沉头螺栓连接，传力过程中引入的二次弯矩使得连接结构的设计更加保守，进一步限制了复合材料减重优势的发挥。虽然复合材料的损伤很难直接观察到，但数值模拟方法有助于更好地分析复合材料的损伤演化过程。因此，建立精确的复合材料连接结构损伤演化模型十分重要。

在过去几十年里，众多学者对复合材料的损伤规律进行了深入的研究。Hill[2]和Tsai等[3]最先以金属等各向同性材料为基础，提出了Tsai-Wu和Tsai-Hill失效判据，这些简单的失效准则不考虑复合材料失效模式的多样化，但考虑了复合材料的正交各向异性特性。虽然这两种准则都能在一定程度上预测复合材料的失效，但并不能分析损伤对材料刚度退化的影响。后来，学者们提出了考虑不同破坏模式（纤维、基体）的失效模型，其中，Hashin[4-5]的失效模型运用最为广泛。与Tsai-Wu和Tsai-Hill准则不同的是，Hashin准则不仅区分失效模式，而且在判断损伤起始后，根据计算得到的损伤变量值来降低损伤点的刚度。目前，仍然有众多学者基于Hashin准则进行复合材料的损伤演化分析。Fang等[6]采用Hashin三维渐进损伤模型对三维编织复合材料代表性体积单元（RVC）的损伤及扩展进行了分析，并根据主要破坏模式讨论了三维四向编织复合材料的非线性行为。Su等[7]对复合材料开孔板的拉伸失效进行了模拟，同时采用界面单元预测层合板的分层失效，得到了与实验吻合良好的结果。

在复合材料连接结构的研究中，McCarthy等[8-9]建立了复合材料凸头螺栓连接的三维有限元模型，并研究了螺栓孔间隙对连接结构力学性能的影响。Qin等[10]对比研究了沉头和凸头连接对复合材料双搭接结构强度、刚度和破坏模式的影响，分析了沉头连接结构弱于凸头连接结构的主要原因，并通过有限元方法分析了螺栓预紧力和间隙配合对两种搭接结构承载能力的影响。Joseph等[11]采用内裂纹带模型对复合材料沉头螺栓连接结构进行了详细的渐进损伤和失效分析，验证了该模型的有效性。Mandal等[12]建立了纤维增强复合材料多钉连接结构的三维渐进损伤模型，并研究了螺栓直径以及螺栓预紧力对结构承载能力的影响。黄文俊等[13]计算了复合材料层合板单钉沉头螺栓连接结构的条件挤压载荷，分析了接触面摩擦、螺栓刚度和连接金属板刚度等因素对连接结构拉伸性能的影响。刘向东等[14]研究了层合板钉孔挤压损伤后剩余刚度的变化规律，提出在模拟挤压失效过程中采用模量先突减、然后逐渐提升的刚度修正方法。李星等[15]预测了机翼翼根后梁下缘条对接件模型的极限强度，发现材料非线性对计算结果的影响最为显著，而网格密度、温差等对计算结果的影响较小。何柏灵等[16]建立了T800级复合材料螺栓单剪连接的强度估算策略，并和实验结果对比证明了该估算策略的可行性。姜晓伟等[17]研究了间隙与干涉两种配合方式对接头刚度的影响，结果表明间隙配合会降低复合材料单钉单剪螺栓连接结构的接头刚度，而0.5%钉直径的干涉量则可以有效提高连接接头刚度。周龙伟等[18]建立了一种新的单向纤维增强树脂基复合材料的刚度突降退化模型，并用该模型对典型复合材料螺栓连接结构的拉伸失效行为进行分析，验证了该模型的计算精度和有效性。

本工作建立复合材料沉头螺栓连接结构的渐进损伤模型，利用改进的三维Hashin失效起始判据和刚度退化方式对结构进行损伤演化分析，并通过编写UMAT子程序对复合材料本构关系进行实现，同时采用黏性正则化方法改进数值算法的收敛性。最后将数值结果与实验数据进行比较，为后续相关研究提供参考。

1 渐进损伤理论

1.1 材料本构模型

复合材料层合板是典型的正交各向异性材料，其主坐标系下单层板的应力应变关系为：

其中矩阵C表示刚度矩阵，如式（2）所示：

式中：C11=E11（1-ν23ν32）/∆，C12=E22（ν12+ν13ν32）/∆，C13=E33（ν13+ν12ν23）/∆，C22=E22（1−ν13ν31）/∆，C23=E3（ν23+ν21ν13）/∆，C33=E33（1−ν12ν21）/∆，C44=G12， C55=G13， C66=G23， ∆= 1−ν12ν21-ν23ν32−ν13ν31−2ν21ν32ν13。E11、E22、E33分别为 1（轴向）、2（横向）、3（面外）方向的弹性模量；G12、G13、G23分别为 12、13、23面的剪切模量；ν12、ν13、ν23分别为 12、13、23面的主泊松比。

由于复合材料层合板的横向各向同性特性，通常认为 E22=E33，G12=G13，ν12=ν13。因此定义材料本构关系仅需材料参数 E11、E22、G12、G23、ν12和 ν23。

1.2 损伤起始判据

采用三维Hashin失效起始判据对复合材料进行损伤判断，并将复合材料的损伤模式分为以下7种，一旦下列方程左边的值等于1，即认为复合材料开始出现相应的损伤形式。

纤维拉伸损伤（σ11>0）：

纤维压缩损伤（σ11<0）：

基体拉伸损伤（σ22>0）：

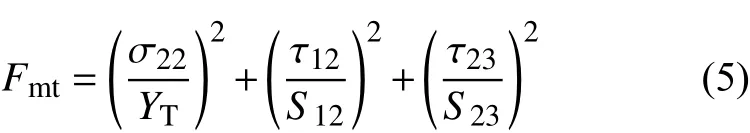
基体压缩损伤（σ22<0）：

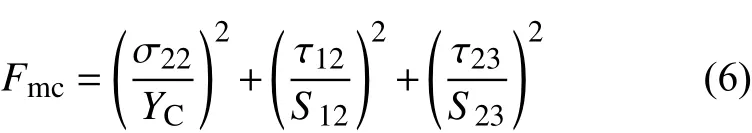
拉伸分层损伤（σ33>0）：

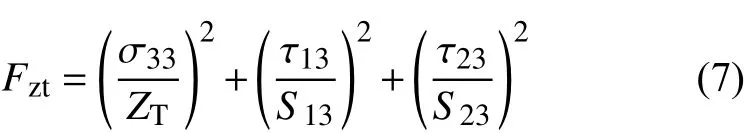
压缩分层损伤（σ33<0）：

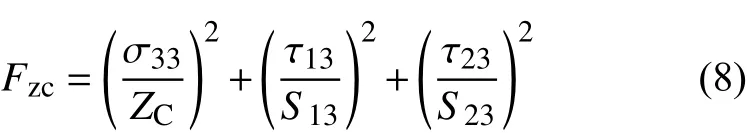
纤维基体剪切损伤（σ11<0）：

式中：XT和XC分别表示纤维方向的拉伸和压缩强度；YT和YC分别表示基体方向的拉伸和压缩强度；ZT和ZC分别表示面外方向的拉伸和压缩强度；S12、S13和S23分别表示 12、13、23面的剪切强度。

1.3 损伤演化模型

当材料达到损伤起始点后，需要对材料的刚度矩阵进行退化。目前，运用比较广泛的几种退化模型有直接刚度降模型、指数型退化模型以及线性退化模型。线性退化模型基于Bažant等[19]提出的断裂带理论，当复合材料的成分失效时，单元耗散能等于其弹性能，材料的损伤均匀地分散在单元上，表现为材料刚度在单元体积上的均匀退化，其示意图见图1。但由于能量耗散随着网格的细化而减小，所以数值解与单元尺寸密切相关。为了减轻模型的网格依赖性，学者们[20-23]在损伤演化表达式中引入了等效位移的概念来计算材料退化过程中的能量耗散：

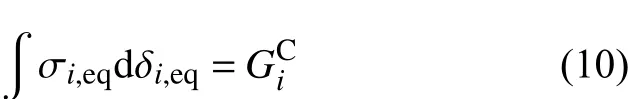
式中：i=ft，fc，mt，mc，zt，zc，fms（下同）；表示不同破坏模式下的断裂韧度；和表示几种损伤模式下的等效位移和等效应力。表1列出了几种损伤模式下等效位移的计算形式，其中LC表示单元的特征长度，对于三维实体单元，，其中Ve表示单元的体积。εjj，eq表示三个主方向的等效应变，定义如下式：

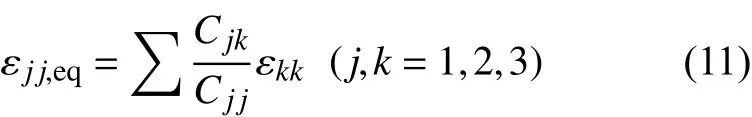
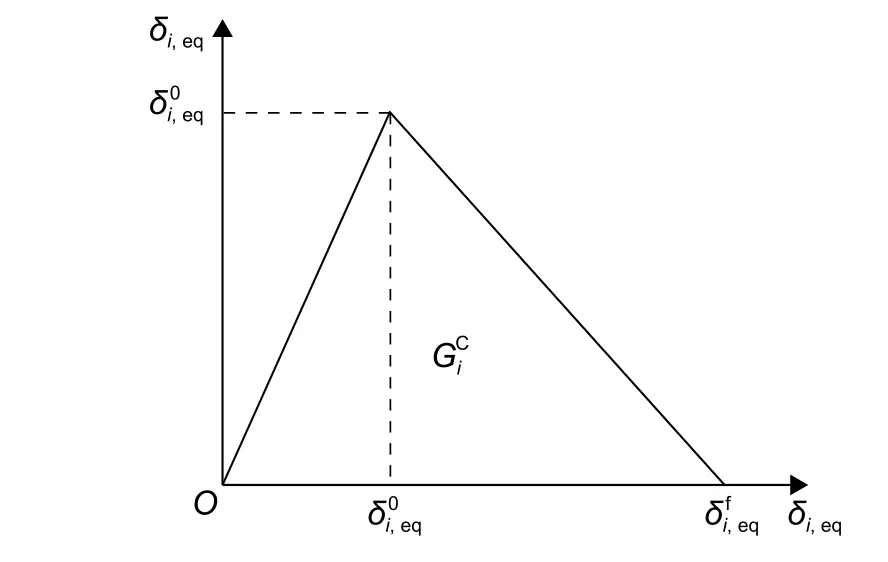
图1 线性退化模型示意图Fig.1 Schematic diagram of linear degenerate model

根据本构关系，也可将其表示为：

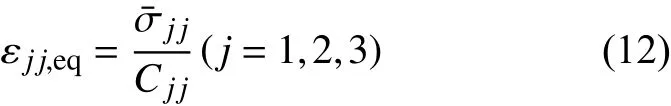
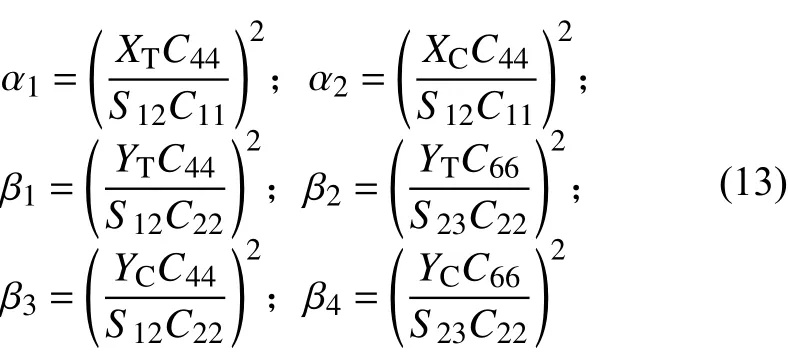
引入α1、α2、β1、β2、β3、β4这几个参数的好处是可以将失效起始判据与损伤演化模型紧密联系起来，当刚好满足某一失效起始条件时，此时的等效失效起始应变表示为：

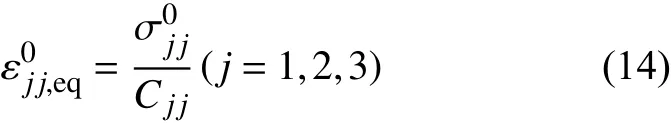
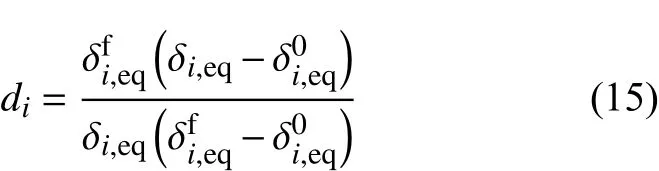
表1 不同失效模式下的等效位移Table1 Equivalence displacements corresponding to different failure modes

在ABAQUS隐式求解过程中，对单元刚度矩阵进行折减常常会导致计算收敛困难，故参照Lapczyk等[22]采用黏性正则化方法来提高计算的收敛性。加入黏性系数可以使软化过程中材料的切线刚度矩阵在足够小的时间增量下是正定的，因而有利于计算的收敛，但过大的黏性系数值往往会导致计算结果失真。因此，通常采用较小（相对于特征时间增量）的黏性系数值，这样既有助于提高模型在退化状态下的收敛速度，也不影响计算结果的精确性，采用黏性正则化后的损伤变量由式（18）计算：

对式（18）离散化，可得到t+Δt时刻的黏性损伤变量为：

引入黏性系数会使计算过程中产生黏性耗散能：

得到材料的损伤变量后，需对材料的刚度进行折减。参考文献[6，25-26]后采用以下的刚度折减方案，折减后刚度矩阵表达式如下：

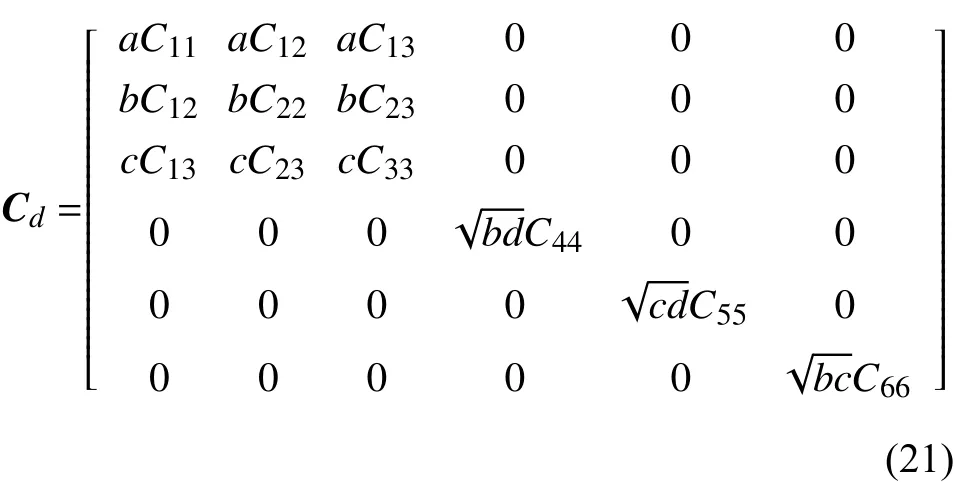
表2 各损伤状态变量的最大值Table2 Maximum value of each damage status variable

2 实验

2.1 试件

参照ASTM D5961设计试件，通过高锁螺栓将两块复合材料层合板搭接，层合板材料为国产T800级碳纤维增强环氧树脂复合材料（CCF800/AC531）和碳纤维斜纹织物，铺层顺序为[45*/−45/90/45/0/−45/0/45/0/−45/0/45/−45/]s。其中，45*铺层为碳纤维斜纹织物层，其单层名义厚度为0.22mm；带横线上标的90°铺层表示对称铺层的中心层，除织物外共25层，层合板单层名义厚度为0.14mm。沉头抗剪高锁螺栓的材料为Ti6Al4V，沉头角为100°。螺栓和孔之间为理想紧配，并施加7.2N•m的预紧力将其紧固，并于两板内侧粘贴同属性同厚度的垫板以保证实验过程中试件的对中性。试件具体尺寸值及贴应变片位置如图2所示。

2.2 拉伸实验

拉伸实验在DNS300液压伺服电子万能试验机上进行。试件通过液压夹头夹持在试验机上，上下夹持长度均为粘贴垫板的长度，采用位移控制加载，加载速率为1mm/min。用试验机传感器记录拉伸载荷，载荷误差在示值的±1%以内；使用与试验机同一厂家的引伸计测量孔边挤压应变，其标距为50mm；用DH3820N静态应变测试分析系统监控试件表面关键性部位的应变，重复测试3个试件。实验现场照片见图3（a），螺栓断口照片见图3（b），搭接面的损伤状态见图 3（c），外表面（非搭接面）的损伤态见图 3（d）。

3 数值分析

用商业有限元软件ABAQUS建立三维连续损伤有限元模型，预测其失效强度并分析损伤形式。复合材料层合板和钛合金螺栓均采用实体单元建模，单元类型均选用C3D8R。参考文献[16，27]，复合材料单层板和碳纤维斜纹织物的力学性能见表3；钛合金螺栓的弹性模量和泊松比分别为110GPa和0.33，参照文献[28-29]定义钛合金螺栓的Johnson-Cook塑性模型和Ductile失效模型。

图2 试件尺寸及贴应变片位置示意图Fig.2 Schematic diagram of specimen size and position of strain gauge

图3 实验照片及断口 （a）实验设备；（b）螺栓断口；（c）搭接面状态；（d）外表面状态Fig.3 Exprimental photographs and fractures （a）test device；（b）bolt fracture；（c）lap surface status；（d）outer surface status

网格质量严重影响计算结果，需对特定区域进行合适的网格划分。“危险”区域为孔边应力集中处，远离孔边处几乎未观察到损伤现象，所以在近孔处加密网格，并采用网格过渡的方式在远孔处（夹持段）划分较为稀疏的网格。经过计算验证，这样不仅可保证结果的精确性，还可以有效加快计算速度。在厚度方向上每层划分一个单元，以保证得到每层单元的应力状态和损伤情况。另外，对螺栓螺纹采用简化方式建模，以间隔式的三角槽代替螺杆上的螺纹，并在螺母中建立与螺杆匹配的内螺纹。在螺栓与层合板接触的区域尽可能保证接触对之间的网格吻合度，网格划分后的模型见图4。

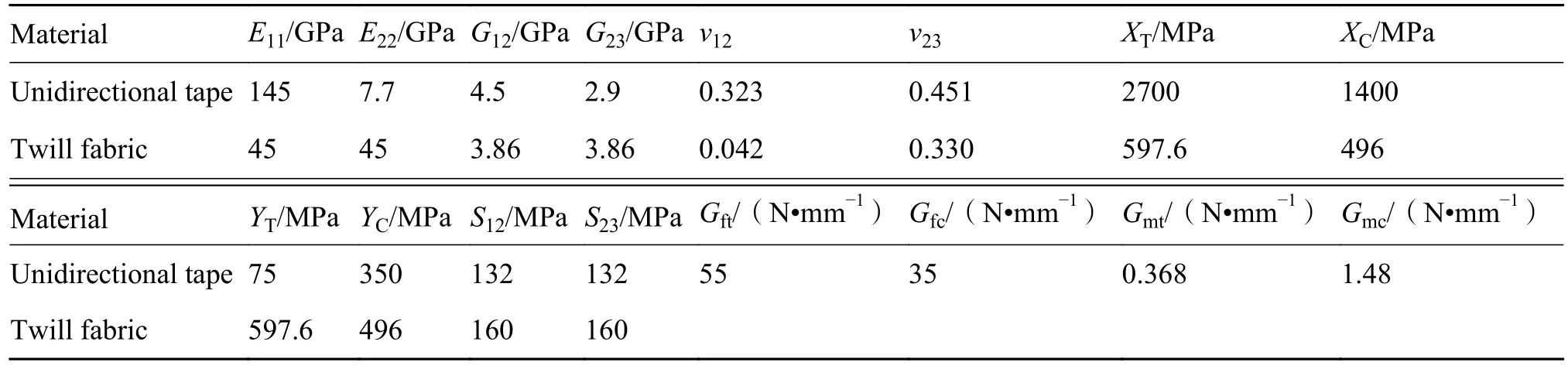
表3 碳纤维增强复合材料单层板和斜纹织物的力学性能Table3 Mechanical properties of carbon fiber reinforced composite laminate and fiber twill fabric

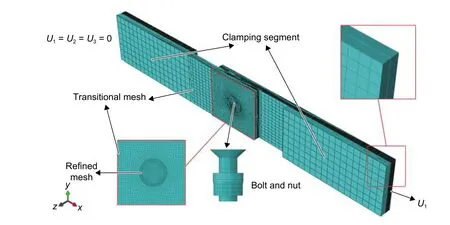
图4 有限元模型及网格Fig.4 Finite element model and mesh

垫板与主板之间采用“tie”绑定约束，两板之间、板与螺栓、板与螺母、螺栓和螺母之间的接触面采用有限滑移的面-面接触算法，接触属性为硬接触，摩擦系数采用0.115。边界条件为：模型夹持部分的表面限制横向位移（U2）和面外方向的位移（U3），模型的左端固定，右端施加轴向位移（U1）。

通过软件内置的“Bolt load”功能施加螺栓预紧力，需要注意的是一次施加较大预紧力会导致计算出现收敛性问题，因此在第一个分析步中加入较小的预紧力，并在后续分析步加入全部预紧力。螺栓预紧力Fbolt与拧紧力矩P之间的关系为：

式中：D为螺栓直径；k为拧紧力矩系数；一般取k=0.2[16]。

4 结果与分析

4.1 黏性系数的影响

为了研究清楚黏性系数的取对数值分析结果的影响程度，采用三个常用的黏性系数值0.001、0.0005和0.0001进行数值分析并比较其结果。首先，对几次计算结果的极限载荷值进行比较。三种黏性系数下的载荷位移曲线如图5（a）所示，图中纵轴的载荷表示固定端的轴向支反力，横轴的位移表示加载端的轴向拉伸位移。从图5（a）可以看出，三次数值分析的结果十分接近，极限载荷相差在0.1%以内。其次，对计算耗时进行比较。本次计算均是在Intel（R）Xeon（R）CPU E5-2630v4@2.20GHz（64GB RAM）处理器上运行，黏性系数为0.0001 时计算耗时180h，约是黏性系数为0.0005时的2.3倍，是黏性系数为0.001时的6.6倍。最后，为了验证引入黏性系数对数值分析结果的影响程度，绘制三个黏性系数下计算的总应变能（ABAQUS输出变量ALLSE）和黏性耗散能（ALLCD）随轴向载荷的变化趋势曲线（图 5（b）），从图 5（b）可以看出，整个计算过程中黏性耗散能的值相对于应变能都非常小，黏性系数取0.001时黏性耗散能最大，为0.032J，占应变能的0.43%。因此，可以认为黏性系数的加入对计算结果的影响可以忽略。为保证计算精确度的同时又提高计算效率，推荐取黏性系数η=0.001。

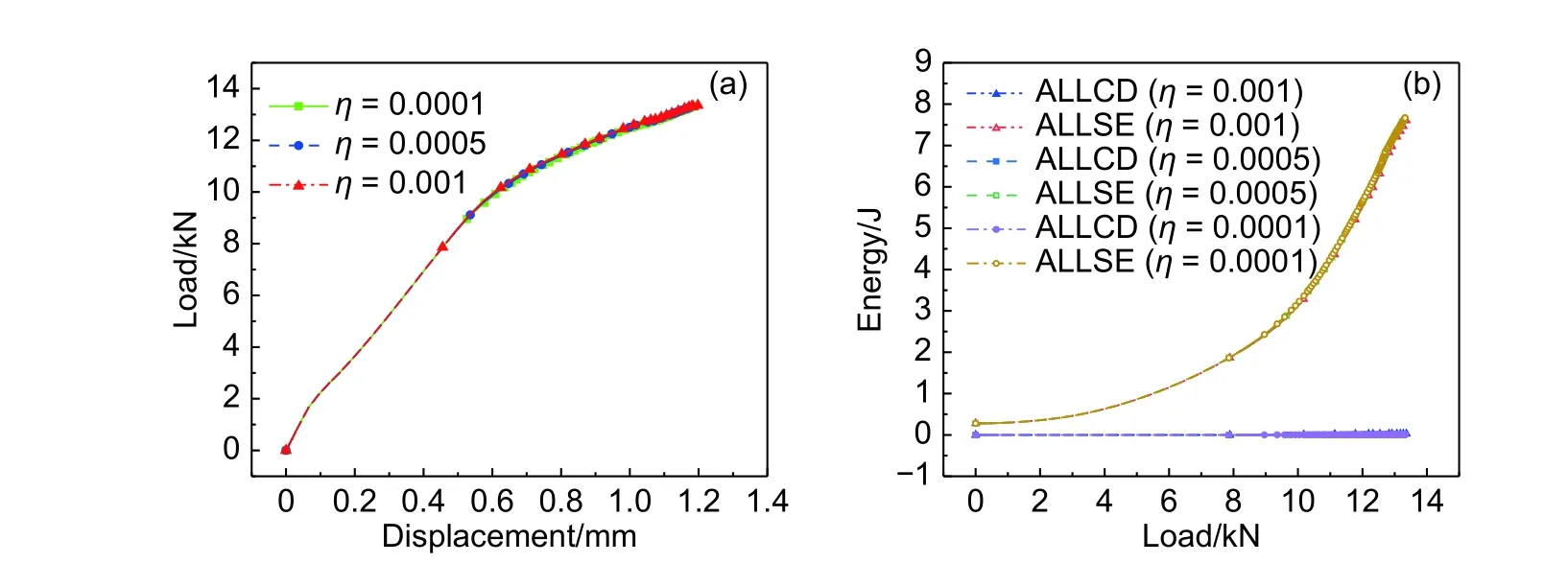
图5 不同黏性系数下的对比 （a）载荷位移曲线；（b）应变能和黏性耗散能Fig.5 Comparison of different viscosity coefficients （a）load-displacement curves；（b）strain energy and viscous dissipation energy

4.2 刚度折减方案的影响

为了提高数值的收敛性，1.3节提出了改进折减刚度矩阵的方法。Fang等[6]在Lapczyk等[22]的基础上将损伤变量的计算形式进行推广，对刚度矩阵的主项（Cij，i=j且 i，j=1，6）进行平方次的折减。而笔者认为主项进行平方次的折减会“加速”材料的失效，尤其是对剪切项的折减过快，会使单元在计算过程中发生严重的扭曲，从而使计算难以收敛。经过多次计算验证，笔者发现对刚度矩阵的次项（Cij，i≠j且 i，j=1，3）进行一次或二次的折减对计算结果影响甚微。在圆孔周围必然存在一些剪应力主导的单元，根据损伤起始判据，剪应力过大会同时使两个方向满足损伤起始条件，如果采用Fang的折减方案，会导致剪切刚度折减过快，因此笔者对剪切项采用了式（21）中开方形式的折减因子。并分别采用改进前后的方案进行计算，得到如图6所示的载荷位移曲线对比图。可以看到，改进前后计算结果十分接近，且改进后模型的计算收敛性更好。从收敛速率上来看，改进前计算到停止共计301个分析步，而改进后仅用110个分析步便到同等分析量。因此，改进刚度折减方案可以明显提高分析计算的效率。

4.3 数值分析与实验结果对比

螺栓连接结构钉孔挤压实验共重复三次，表4列出了三次实验的极限载荷值，其标准差和离散系数都比较小，说明该实验的可重复性非常好。为了和实验数据进行对比，在有限元模型上选取与试件贴应变片位置相同的4处单元，输出其轴向应变，并取单板横截面上的平均应力作为因变量，得到数值分析结果和实验结果的应力-应变曲线对比图（图7）。

图6 载荷-位移曲线对比Fig.6 Comparison of load-displacement curves

表4 各试样的极限载荷值Table4 Ultimate load value of each specimen

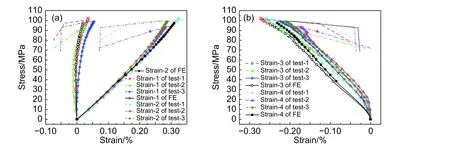
图7 应力-应变曲线 （a）1 号应变片和 2 号应变片；（b）：3 号应变片和 4 号应变片Fig.7 Stress-strain curves （a）strain gauge1#and strain gauge2#；（b）strain gauge3#and strain gauge4#

从图7（a）看出，有限元预测的1号、2号应变片的轴向应变与实验值吻合得非常好。由于单搭接产生的次弯曲效应，使得下搭接板出现向下“弯”的趋势。单纯的弯曲效应会使1号应变片呈现负值，2号应变片呈现正值。因此在此弯曲效应和拉伸载荷的共同作用下，1号应变片附近的应变在整个实验过程中都非常小，实验和有限元结果都在–150～600με之间变化，而即使在应变非常小的情况下，有限元模拟的1号应变值与实测值十分接近。2号应变片的应变相较于1号非常大，应变保持为正值并逐渐增大。对于2号应变，可以看到预测值和三次实验值始终十分接近，载荷为7～8kN时误差最大且不超过3%，说明该模型预测结果的精确性。从图7（b）可以看出3号、4号的应变与实验值相对1号、2号误差略大，原因是3、4号应变片距离孔边较近，应力状态十分复杂，预测难度偏大，但从总体趋势上来看，有限元结果和实验结果仍比较一致。另外需指出的是，当有限元计算到图6中所示的最高载荷时，计算结果不能收敛而停止，此时螺栓上的部分单元已经开始进入失效状态。螺栓的Ductile状态变量（ABAQUS输出变量DUCTCRT）最终状态如图8（a）所示。因为实验过程中一旦螺栓上出现少量裂痕，其在高应力水平下会快速扩展，从而出现螺栓突然断裂的现象；而在ABAQUS隐式分析中，很难模拟该复杂模型的螺栓快速断裂问题。因此，近似地认为有限元分析在出现收敛问题前的最终载荷值即为该连接结构的极限载荷预测值，为13.36kN。该数值结果比三次实验结果的平均值低0.61kN，相对误差为4.4%。

综上可得，模型对复合材料沉头螺栓连接结构失效过程预测较好，可用于分析结构损伤失效。

4.4 损伤失效分析

实验过程中，加载初期载荷平稳上升，两板搭接部分外侧逐渐产生小间隙，板也由平直变得弯曲，说明单搭接的次弯曲效应十分明显。当载荷达到约10kN时能听到“滋滋”的声音，说明此时已发生较为严重的挤压损伤。继续加载，板的弯曲程度不再明显增加，此时孔的挤压损伤进入扩展阶段。直至载荷达到极限值时，随着一声巨响，螺钉断裂，整个结构彻底失去承载能力。从实验结果来看，图3（c）中的搭接面发生了十分严重的挤压损伤，圆孔被拉成了“椭圆状”，从图3（d）中可看出，上搭接板和螺栓头、螺母接触的表面上损伤并不明显，这进一步说明了单搭接中次弯曲导致钉孔处应力不均的问题。

图8（b）为复合材料极限载荷时螺栓的应力云图。可以看出，沉头螺栓单搭接较凸头螺栓单搭接更容易产生应力集中，沉头连接的应力集中主要发生在沉头端和螺纹附近，钉头锥面部分基本没有应力集中，这将导致螺杆与沉头之间应力梯度过大，螺杆顶端更容易发生较大变形，进而导致钉孔间距增大。而且在沉头段斜面的挤压作用下，复合材料板会出现分层损伤形式，这进一步加重了单搭接结构的次弯曲问题，也是沉头连接弱于凸头连接的原因之一。

根据输出变量可以监控几种损伤模式的扩展情况。首先，可以发现最早出现的损伤形式是基体拉伸损伤（图9（a）），其起始位置在上搭接板（带沉头孔）离搭接面最近的90°层上，此时载荷为3.5kN。随着继续加载，该种损伤逐渐向上搭接板的内层扩展，并且下搭接板靠近搭接面的几层也逐渐开始出

图8 沉头螺栓最终状态 （a）DUCTCRT 状态变量；（b）Mises应力Fig.8 Final status of countersunk bolt （a）DUCTCRT status variable；（b）Mises stress

图9 损伤状态 （a）基体初始拉伸损伤；（b）纤维最终拉伸损伤；（c）纤维最终压缩损伤；（d）基体最终拉伸损伤；（e）基体最终压缩损伤；（f）Z向最终拉伸损伤；（g）Z向最终压缩损伤；（h）纤维基体剪切最终损伤Fig.9 Damage status （a）initial tension damage of matrix；（b）final tension damage of fiber；（c）final compression damage of fiber；（d）final tension damage of matrix；（e）final compression damage of matrix；（f）final tension damage ofZ-direction；（g）final compression damage ofZ-direction；（h）final shear damage of fiber-matrix

现基体拉伸损伤和纤维基体剪切损伤形式。然后随着载荷继续增大到5kN左右时，在上搭接板右侧孔边处（靠近加载端）和下搭接板左侧孔边处开始出现纤维拉伸和纤维压缩的损伤形式，且失效都集中在上搭接板孔右侧和下搭接板孔左侧。载荷为7kN到11kN时为损伤快速扩展时间段，此时复合材料层合板的各损伤变量迅速达到最大值并向周边扩展，同时螺栓的Ductile状态变量也出现正值并逐渐上升。当载荷达到12kN时，复合材料板损伤扩展进入缓慢阶段，而此时螺栓开始进入损伤积累阶段，直至载荷达到极限值时计算出现收敛性问题而停止。在到达极限载荷时，整体的几种损伤状态如图9（b）～（h）所示，可以看出损伤部位主要为上搭接板右侧和下搭接板左侧的挤压区。另外，由于加载过程中导致螺栓偏斜，因此上搭接板左侧局部也出现了Z向压缩损伤的情况，而整个过程中并没有Z向拉伸损伤形式的出现。对比前面的试件断口照片，可以看出仿真得到的损伤区域和试验结果吻合良好。

4.5 挤压强度分析

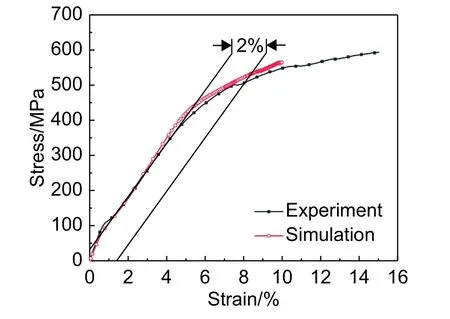
图10 挤压应力-应变曲线Fig.10 Bearing stress-strain curve

5 结论

（1）基于渐进损伤理论，建立了复合材料沉头螺栓连接的三维连续损伤有限元模型，采用三维Hashin失效准则进行损伤起始判断，提出一种新的材料损伤后刚度折减方案。就破坏载荷而言，三次实验结果十分接近，且实验平均值与数值分析结果误差为4.4%。而实验与数值分析的载荷-应变曲线、挤压应力-应变曲线也基本吻合，说明了基于连续损伤力学的有限元模型是可靠的。

（2）在渐进损伤理论中，提出了改进后的等效位移表达式和刚度矩阵退化方式，可以有效提高数值计算的收敛性；并考虑了引入黏性系数对数值计算结果的影响，发现当黏性系数为0.001时系统的黏性耗散能占应变能比值低于0.5%，因此推荐取该黏性系数值。

（3）采用数值模拟方法对复合材料沉头螺栓连接结构的失效行为进行分析，发现复合材料板的损伤以孔两侧的挤压损伤为主，同时伴随着局部的其他损伤形式，其中带沉头孔的层合板损伤更为严重，结构最终破坏模式是沉头螺栓在螺杆螺纹处被剪断，而在螺栓断裂之前，搭接板已经超过了其2%偏移挤压强度值，因此，该搭接结构设计是合理的。