航天器多约束姿态机动时-虚混合域规划方法
2020-12-07朱圣英梁子璇
王 辉,徐 瑞,朱圣英,梁子璇
(1.北京理工大学宇航学院,北京 100081;2.深空自主导航与控制工信部重点实验室,北京 100081)
0 引 言
在轨运行的航天器经常需要进行姿态机动来完成特定的任务,例如通信、观测和跟踪。航天器上的燃料和电能都是有限的;因此,减少姿态机动过程中的能量消耗对于任务成功执行非常重要。进一步地,空间中存在很多明亮天体,例如太阳、火星和月亮;航天器上的某些光学敏感器(例如星敏感器和红外望远镜)在姿态机动过程中不能曝光于这些明亮天体下,否则可能会损坏。同时,为了保持对地通信,航天器上的天线在姿态机动过程中需要与地面站保持一定的指向关系。另外,陀螺仪和太阳敏感器等仪器都需要航天器的角速度不能太大,否则会造成较差的角速度测量和姿态估计结果;航天器上的执行机构一般只能提供有限的控制力矩。最后,航天器姿态机动过程中还需要满足自身的姿态运动学和动力学约束。
这些约束[1-4]的存在极大地限制了航天器在姿态机动过程中的可行空间,这使得多约束姿态机动规划问题变得难以求解。为了解决多约束姿态机动问题,McInnes[5]使用人工势函数[6-8]的方法,通过对禁忌区域施加高的势能来实现对姿态指向禁忌约束的规避。该方法对计算资源的要求较低,但是未考虑角速度和控制力矩有界约束,且欧拉角的姿态表示方式容易导致奇异性问题。Hablani[9]在单位球上定义排斥区域,并主要通过求解两个相关转角得到理想的切线路径来规避明亮天体,即需要的俯仰/偏航转角和明亮天体相对于旋转平面的排斥角。该方法简单直观,但是只适合于处理少量指向约束的情况。Frazzoli等[10]应用随机规划[11-12]方法求解该问题,可以快速搜索得到可行的姿态路径。该方法能处理复杂指向约束的情况,但是随机算法具有很大的不确定性,星上应用不可靠。Kim等[13]将禁忌约束转化成二次凸约束的形式,并将边界条件表示成二次型形式的目标函数,而后利用半定规划[14-15]方法求解得到满足约束的姿态机动轨迹。该方法采用单步规划,且未考虑性能指标优化。Kjellberg等[16]利用二十面体离散化方法和A*搜索算法求解复杂指向约束下的姿态机动可行路径。该姿态路径规划算法未考虑姿态动力学和有界约束。Biggs等[17]提出了一种半解析的几何姿态运动规划方法来同时处理禁忌约束和有界约束。该方法通过改变路径参数来生成不同的姿态路径,规避禁忌约束;同时,利用时间参数化的方法来改变机动角速度,并实现满足有界约束。该方法计算代价较小,但是只适合处理简单的小范围禁忌区域的情况。
在考虑多种复杂约束的情况下,姿态机动规划问题已经很难求解。引入能量消耗这一优化指标,又进一步给问题带来一个巨大的挑战。Sun等[18]利用半定松弛方法将原来的非凸二次约束二次规划问题转化为半定规划问题,并通过迭代秩最小化方法逐渐得到最优解,实现了复杂指向约束下能量最优姿态机动。武长青等[19]引入线性松弛方法将原问题转化为双线性规划问题,并通过求解其中一个变量的凸包络和凹包络,得到原问题的一个线性松弛解,最后通过基于评价函数的迭代规划算法求出原问题的近优解,实现了复杂指向约束下低能量姿态机动。Wu等[20]利用改进的差分进化算法来得到复杂约束下姿态机动近优解。这些方法计算效率较低,难以实现星上应用。伪谱法[21-23]是一种求解优化问题的直接法,广泛应用于多种轨迹规划问题。该类方法利用正交多项式来表示最优解曲线,将原来的最优控制问题转化为求解正交多项式展开系数的非线性规划问题。伪谱法采用了非一致节点离散化方法,只需少量的节点就可以完成对优化问题的离散化。但是,伪谱法只能保证在节点处满足指向约束,而并未考虑中间稀疏节点之间的路径是否满足约束。而且当节点个数增加时,伪谱法的计算效率会显著降低。
本文首先提出了时-虚混合域的概念,而后采用连续的路径和时间参数化,建立了时-虚混合域上非线性约束问题模型,提出了时-虚混合域单点式非线性姿态机动规划方法,解决了文献[17]中方法只适合处理简单的小范围禁忌区域的问题,并且有效减少了航天器姿态机动中的能量消耗,实现了连续光滑的多约束低能量姿态机动的高效规划。
1 航天器姿态机动中的多种复杂约束
用旋转矩阵表示航天器的姿态,刚体航天器的姿态运动学方程[17,24]可以表示如下:
(1)
式中:CIB表示从本体坐标系到惯性坐标系的旋转矩阵,如式(2)所示。ω=[ω1,ω2,ω3]T表示本体坐标系下航天器的角速度。x×表示由x=[x1,x2,x3]T定义的斜对称矩阵,如式(3)所示。q=[q0,q1,q2,q3]T是单位四元数,表示从本体坐标系到惯性坐标系的旋转。q0是标量部分。

(2)
(3)
刚体航天器的姿态动力学方程[25-26]如下所示:
(4)
式中:u=[u1,u2,u3]T表示本体坐标系下的控制力矩。J∈R3×3表示航天器的惯量矩阵。如果本体坐标系是主轴坐标系,则有J=diag(J1,J2,J3)。
在实际工程应用中,航天器上测量仪器的量程有限;某些仪器的正常工作需要航天器的角速度不能太大;执行机构提供的控制力矩是有界的。这形成了航天器姿态机动过程中的角速度和控制力矩有界约束[25-26],可以分别表示为如下不等式的形式。
|ωj|≤ωmax,j=1,2,3
(5)
|uj|≤umax,j=1,2,3
(6)
式中:ωj和uj为分量约束的角速度和控制力矩。如果对整体矢量有约束,则可以将约束表示为角速度和控制力矩的2范数的形式。

图1 禁忌约束
(7)



图2 强制约束
(8)

姿态机动初始和终端边界条件可以归纳为如下形式:
(9)

2 时-虚混合域单点式非线性姿态机动规划方法
为了解决多约束低能量姿态机动规划问题,本文提出了时-虚混合域的概念和时-虚混合域单点式非线性姿态机动规划方法。时-虚混合域的含义如定义1所示。时-虚混合域模型采用连续参数化的虚拟域解析路径集以及时域角速度和控制力矩来描述两点间姿态机动,而后通过统一的非线性参数优化和单点式路径分解置换规划求解得到复杂多约束下低能量姿态机动轨迹以及连续光滑的角速度和控制力矩曲线。
定义1.时-虚混合域指的是时域和虚拟域同步存在而形成的定义域。具体地对于姿态机动问题而言,在虚拟域上描述姿态机动路径,在时域上描述角速度和控制力矩,并且姿态机动路径以及角速度和控制力矩的求解过程同步进行。
2.1 时-虚混合域上非线性约束问题建模

(10)
其中,CW(p)=[xyz],如式(11)~式(13)所示:
(11)
(12)
(13)
式中:


M1(p)=Asech(γp+C)
M2(p)=Bsech(γp+C)








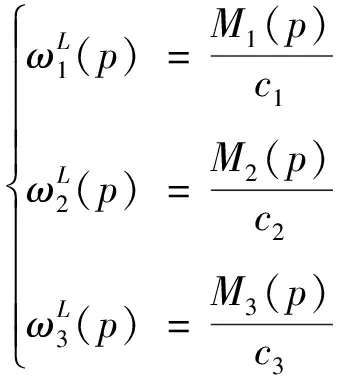
(14)

(15)
(16)
不同于文献[17]中首先求解虚拟域姿态机动路径而后通过调整机动时间来改变角速度和控制力矩进而满足有界约束的方法,本文提出了时-虚混合域的概念,统一优化求解虚拟域姿态路径以及时域角速度和控制力矩。时-虚混合域模型在保持路径和时间参数化所带来的问题降维和约束解耦等优点的基础上,通过统一同步优化机制,进一步增加了优化的全局性,以实现更好的目标优化。

(17)
(18)
2.2 单点式路径分解置换规划方法
通过对式(18)建立的时-虚混合域上非线性约束问题的参数优化,可以得到连接任意的起始和目标姿态的虚拟域路径以及时域角速度和控制力矩。如果该路径违反指向约束,则选取约束违背路径区域中间位置对应的最近临界增量节点[25]作为路径分解置换节点。而后同样根据式(18)依次求解各段姿态机动。每段姿态路径如果再次违反指向约束,则需要再次进行单点式路径分解置换。单轴禁忌约束下单次单点式路径分解置换如图3所示。图中实线圆包围起来的部分为禁忌区域;虚线边界圆通过给禁忌约束增加最近临界增量角得到;从起点到目标点的箭头虚线是分解置换前的路径;从起点到目标点的箭头实线是分解置换后的路径;箭头虚线上的五角星节点是当前约束违背路径区域中间位置节点;箭头实线上的六角星节点是当前路径分解置换节点。

图3 单轴禁忌约束下单次单点式路径分解置换
特别地,最近临界增量节点指的是在增量圆锥边界上跟当前位置节点角度距离最近的节点。增量圆锥通过在指向约束角的基础上叠加一个增量角度得到。该增量角度对于禁忌约束为正值,对于强制约束为负值。根据从当前位置节点到最近临界增量节点的欧拉旋转的姿态关系,可以得到最近临界增量节点的求解方法如式(19)所示,详细的过程可以参考文献[25]。
(19)

2.3 算法流程
本文时-虚混合域单点式非线性姿态机动规划方法的算法流程如图4所示,算法步骤如下。
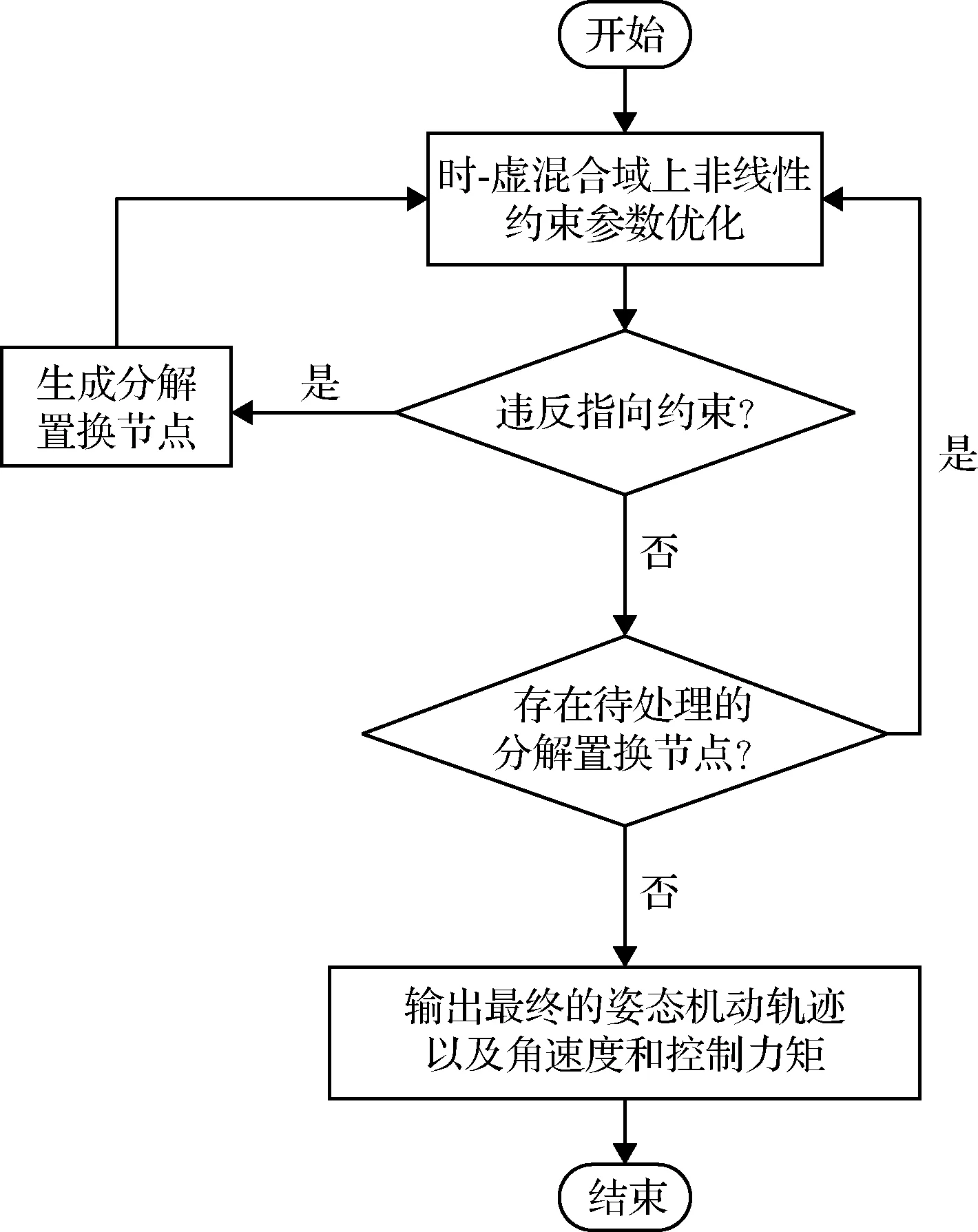
图4 时-虚混合域算法流程图
步骤1:求解式(18)所示的时-虚混合域上非线性约束问题,得到当前段姿态路径以及角速度和控制力矩。
步骤2:判断该段路径是否违反指向约束;否,执行步骤7;是,得到指向约束违反区域个数N,执行步骤3。
步骤3:对于每块指向约束违反区域,生成相应的路径分解置换节点。
步骤4:根据式(18)建模并求解出本段姿态路径以及角速度和控制力矩;再判断本段路径是否违反指向约束;否,执行步骤5;是,重复步骤3~6。
步骤5:根据式(18)建模并求解出下一段姿态路径以及角速度和控制力矩。
步骤6:然后再判断下一段姿态路径是否违反指向约束;否,重复步骤5到6,直到求解出全部N+1段姿态路径以及角速度和控制力矩,执行步骤7;是,重复步骤3~6。
步骤7:输出最终的姿态机动轨迹以及角速度和控制力矩。
3 仿真与分析
本节分别进行单轴禁忌约束以及多轴禁忌和强制约束仿真来说明本文方法的有效性和优势。仿真在普通的台式电脑(3.00 GHz CPU和3.00 GB RAM)上利用MATLAB编程实现。航天器能提供的最大控制力矩为0.1 N·m,允许的最大角速度为0.0471 rad·s-1,基本参数如表1所示。航天器X轴和Y轴正方向上分别安装有一个星敏感器和通信天线。

表1 航天器的基本参数
3.1 单轴禁忌约束
本节首先考虑单轴禁忌约束的情况。在姿态机动过程中,星敏感器需要规避四个明亮天体禁忌约束,相关参数如表2所示。姿态机动的初始和终端边界条件如式(20)所示。

表2 禁忌约束参数
(20)
本文方法求得的星敏感器视线轴(X轴)在惯性坐标系下经纬度形式的机动轨迹如图5所示。图中连接起点到目标点的实线是求得的机动轨迹,密集圆点包围起来的部分是由禁忌约束产生的禁忌区域。其中,对于惯性坐标系下任意的单位矢量y∈R3,相应的经纬度计算如式(21)所示。从图5可以看出,本文方法可以有效地得到安全规避多个禁忌约束的姿态机动轨迹。

图5 X轴的机动轨迹

(21)
式中:y=[y1,y2,y3]T,lo和la分别表示经度和纬度。
机动过程中角速度和控制力矩随时间变化的曲线分别如图6和图7所示。从图6~7可以看出,本文方法在单轴禁忌约束下求得的角速度和控制力矩都满足有界约束,而且角速度曲线连续光滑,控制力矩曲线连续且分段光滑。

图6 角速度曲线

图7 控制力矩曲线
本文方法的平均规划时间是3.98 s,如表3所示。本文方法求得的姿态机动的能量消耗是0.0038 N2·m2·s。相同条件下,基于MATLAB GPOPS工具箱的伪谱法[21-23,26,29]的平均规划时间是15.93 s。伪谱法求得的姿态机动的能量消耗是0.0109 N2·m2·s。本文方法的规划时间比伪谱法减少了75%,并且求得的姿态机动的能量消耗比伪谱法减少了65%。本文方法在单轴禁忌约束下可以快速地得到低能量的姿态机动规划结果。

表3 时-虚混合域方法和伪谱法的规划结果
3.2 多轴禁忌和强制约束
本节进一步考虑更加复杂的多轴禁忌和强制约束情况。在姿态机动过程中,天线需要保持与地面站通信,同时星敏感器需要规避四个明亮天体禁忌约束,相关参数如表4所示。姿态机动的初始和终端边界条件如式(22)所示。

表4 指向约束参数

(22)
本文方法求得的星敏感器视线轴(X轴)在惯性坐标系下经纬度形式和通信天线(Y轴)在惯性坐标系下三维空间的机动轨迹以及角速度和控制力矩随时间变化的曲线分别如图8~图11所示。图8的经纬图的含义和图5相同。图9中圆锥包含的部分是由强制约束产生的强制区域。从图8和图9可以看出,本文方法求得的姿态机动轨迹在安全规避多个禁忌约束的同时可以实现满足强制约束。从图10和图11可以看出,本文方法在非常复杂的多轴禁忌和强制约束下同样可以得到满足有界约束的角速度和控制力矩,而且角速度曲线连续光滑,控制力矩曲线连续且分段光滑。

图8 X轴的机动轨迹

图9 Y轴的机动轨迹
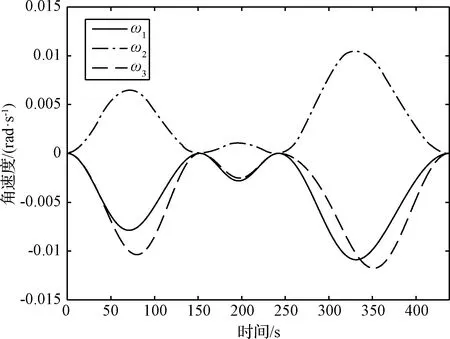
图10 角速度曲线

图11 控制力矩曲线
对于非常复杂的多轴禁忌和强制约束仿真,本文方法的平均规划时间和求得的姿态机动的能量消耗分别是7.26 s和0.0042 N2·m2·s,见表5。相同条件下,伪谱法的平均规划时间和求得的姿态机动的能量消耗分别是30.85 s和0.0253 N2·m2·s。本文方法的规划时间和求得的姿态机动的能量消耗比伪谱法分别减少了76%和83%。本文方法在更加复杂的多轴禁忌和强制约束下同样可以实现低能量姿态机动的快速规划。

表5 时-虚混合域方法和伪谱法的规划结果
4 结 论
针对复杂禁忌和强制约束下低能量姿态机动规划问题,本文提出了时-虚混合域的概念和时-虚混合域单点式非线性姿态机动规划方法。时-虚混合域建模采用虚拟域姿态机动路径集合以及时域角速度和控制力矩。在时-虚混合域模型的基础上,采用非线性参数优化和单点式路径分解置换规划方法求解问题。仿真结果表明该方法能高效地处理多种复杂约束,并且有效地减少姿态机动过程中的能量消耗,得到连续光滑的低能量姿态机动规划结果,有利于实际工程应用。
