谈多项式乘多项式之“田”字模型算法

郑月群

摘要：多项式相关计算是初中阶段数学《数与式》知识模块中的一个重要组成部分，而多项式的乘法计算又是其中较重要的内容，所以多项式乘多项式的计算技能显得尤其重要。本文由多项式乘多项式的几何意义转化为一种形式的计算方法，有效避免计算中易错情况，提高计算的准确度，并提升学生的计算能力。

关键词：多项式;田字模型;算法;方程思想

多项式乘多项式计算结果的准确度是计算能力高低的有力体现。学好了，可以提升计算能力;学不好，让你怀疑人生。实践证明，学生学习多项式乘多项式之后，常出现漏乘或重复乘、符号出错而导致计算错误等问题。为了帮助学生有效克服以上出现的问题，笔者可谓绞尽脑汁。在一次设计教学情境时刚好用到长方形的面积计算，笔者突发联想到一种计算多项式乘多项式的方法，并应用于课堂教学中，收到很好的效果，也证实这种计算方法是可行的。于是，笔者在已学单项式乘以单项式、合并同类项的基础上设计，让学生从长方形面积计算的情境中引出多项式乘多项式的几何意义，探究发现计算的规律，模拟出“田”字模型，利用模型的知识，通过例题、变式练习形成计算的技能，从而提升计算的能力，达到强化思维的目的。下面一起探讨如何用“田”字模型算法求多项

解：

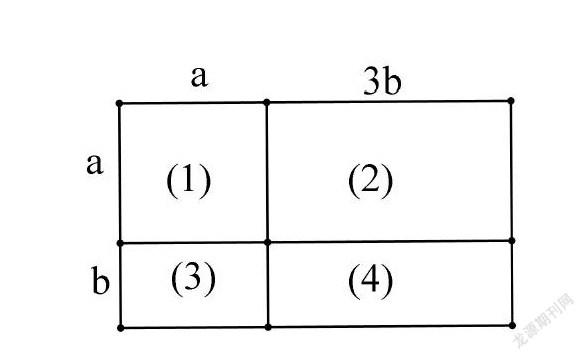
方法1：图形可以看作是一个长为（a+3b），宽为（a+b）的长方形，此长方形草地的面积为（a+3b）.（a+b）.

方法2：图中区域（1）的面积为为a;图中区域 （2）的面积为为3ab;图中区域（3）的面积为ab;图中区域（4）的面积为为36’。故此长方形草地的面积為a+3ab+ab+3b=a+4ab+3b

联合这两种计算的结果，得到等式是（a+3b）·式乘多项式的积。

一、利用多项式乘多项式的几何意义创建模型

（一）利用情景问题深入理解多项式乘多项式的几何意义

如图所示，这是一块长方形草地，小米为了测量它的面积快抓破头了，你快来帮忙想一想办法吧。

思考：怎样计算这个长方形草地的面积？思路分析：用整体计算或分块计算。

第一种整体看大长方形的长为（a+3b），宽为（a+b），用长方形的面积计算公式即可求出长方形草地的面积。

第二种分块计算四个小长方形面积分别为a，3ab，ab，3b，把各小长方形的面积相加即可得草地总面积。

（a +b） =a +3ab+ab+3b =a +4ab+3b

多项式乘多项式的几何意义：多项式乘多项式结果可看作是是一个宽与长分别为两个多项式值的长方形的面积。

上面两种计算方法让学生初步感受到代数与几何的内在联系，体会数形结合数学思想方法。根据学生思考角度也会利用学过的知识如单项式与多项式的乘法法则，乘法分配律等探索得到想要的结论，多角度思考问题有效训练学生的发散思维和分析问题能力。

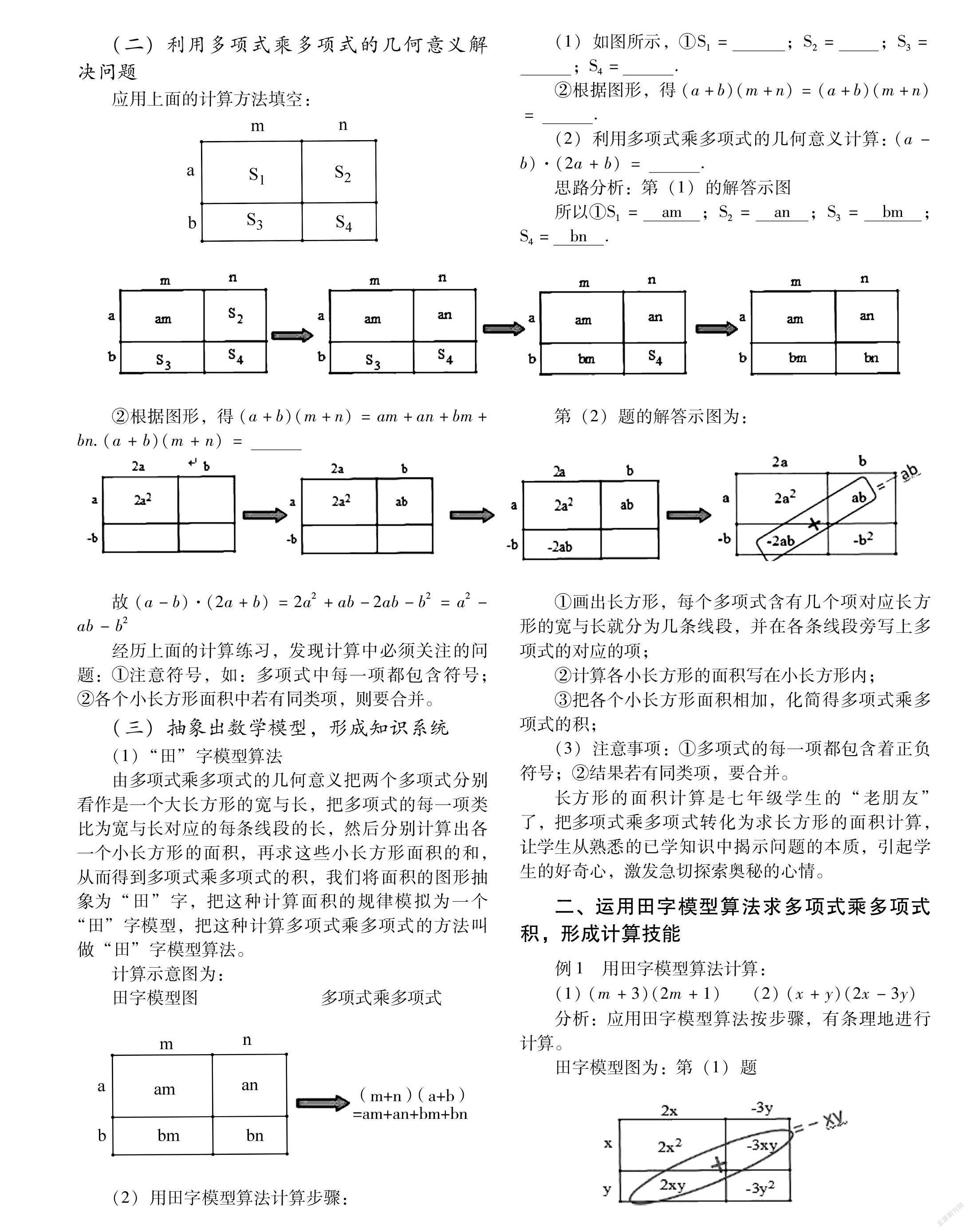
（二）利用多项式乘多项式的几何意义解决问题

应用上面的计算方法填空：

②根据图形，得（a+b）（m+n）=am+an+bm+ bn.（a+b）（m+n）=

故（a-b）.（2a+b）=2a +ab-2ab-b=aab -b2

经历上面的计算练习，发现计算中必须关注的问题：①注意符号，如：多项式中每一项都包含符号;②各个小长方形面积中若有同类项，则要合并。

（三）抽象出数学模型，形成知识系统（1）“田”字模型算法

由多项式乘多项式的几何意义把两个多项式分别看作是一个大长方形的宽与长，把多项式的每一项类比为宽与长对应的每条线段的长，然后分别计算出各一个小长方形的面积，再求这些小长方形面积的和，从而得到多项式乘多项式的积，我们将面积的图形抽象为“田”字，把这种计算面积的规律模拟为一个“田”字模型，把这种计算多项式乘多项式的方法叫做“田”字模型算法。

（2）用田字模型算法计算步骤：

第（2）题的解答示图为：

①画出长方形，每个多项式含有几个项对应长方形的宽与长就分为几条线段，并在各条线段旁写上多项式的对应的项;

②计算各小长方形的面积写在小长方形内;

③把各个小长方形面积相加，化简得多项式乘多项式的积;

（3）注意事项：①多项式的每一项都包含着正负符号;②结果若有同类项，要合并。

长方形的面积计算是七年级学生的“老朋友”了，把多项式乘多项式转化为求长方形的面积计算，让学生从熟悉的已学知识中揭示问题的本质，引起学生的好奇心，激发急切探索奥秘的心情。

二、运用田字模型算法求多项式乘多项式积，形成计算技能

例1用田字模型算法计算：

（1）（m+3）（2m+1） （2）（x+y） （2x-3y）分析：应用田字模型算法按步骤，有条理地进行计算。

田字模型图为：第（1）题

例题的教学能进一步巩固新知，形成技能，熟练应用田字模型算法求多项式乘多项式的积。应用田字模型算法解题时要注意多项式各项的符号和同类项的合并，及转化思想和数形结合思想的运用。

三、变式训练提升计算能力

（一）直接应用田字模型算法求多项式乘多项式的积

点拨：多项式是几项式，所画长方形的宽与长就对应分成几条线段。画计算示意图时注意因式的项数增加导致“田”字的变形，但计算的核心方法不变。田字模型图为：第（1）题

实践教学证明：通过例题1与对应变式练习让学生感受到应用田字模型算法求多项式与多项式的积时能够有效的避免符号出错和漏乘等优化特点。

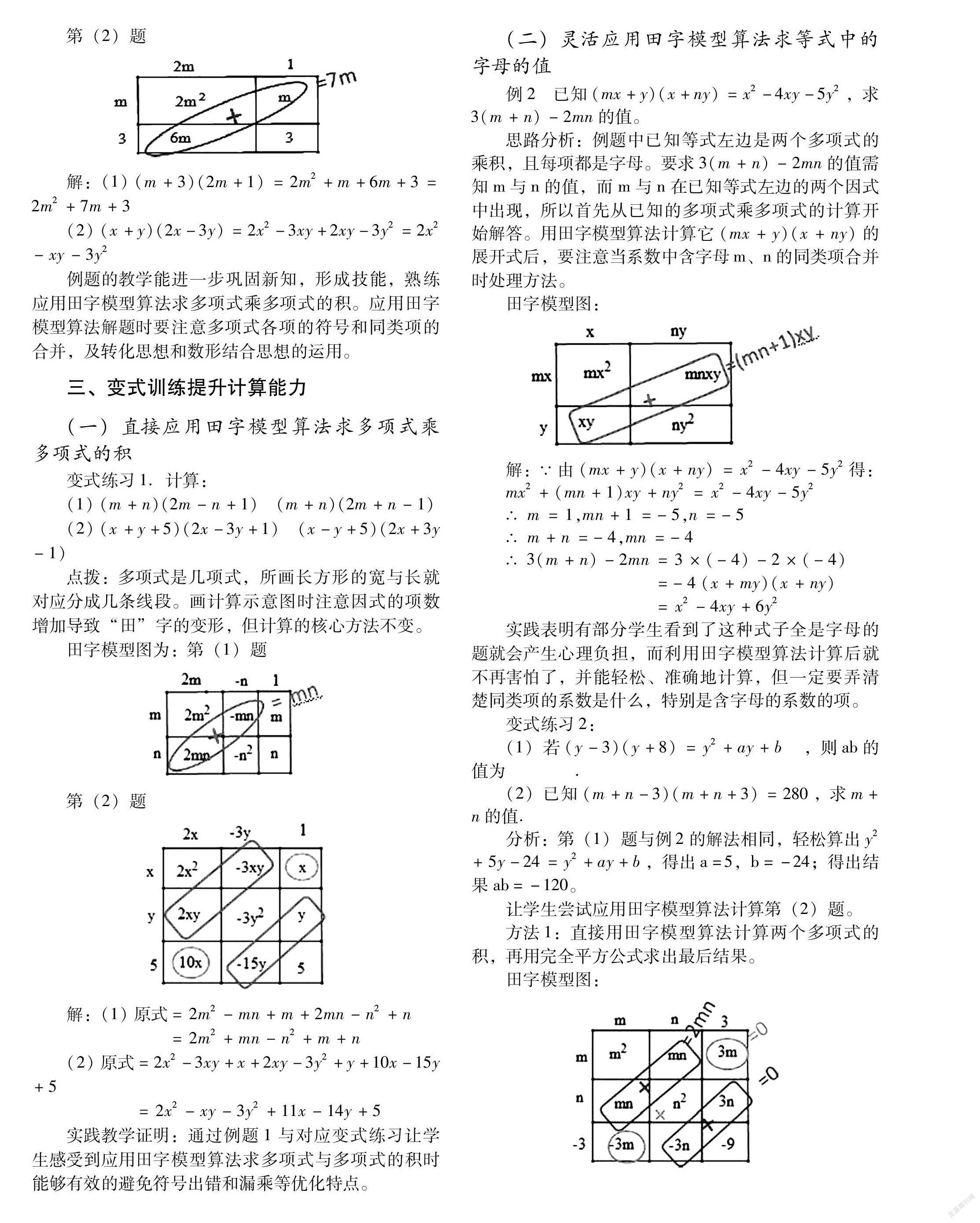
（二）灵活应用田字模型算法求等式中的字母的值

例2已知（mx+y）（x+ny）=x-4xy-5y，求3（m+n）-2mn的值。

思路分析：例题中已知等式左边是两个多项式的乘积，且每项都是字母。要求3（m+n）-2mn的值需知m与n的值，而m与n在已知等式左边的两个因式中出现，所以首先从已知的多项式乘多项式的计算开始解答。用田字模型算法计算它（mx+y）（x+ny）的展开式后，要注意当系数中含字母m、n的同类项合并时处理方法。

田字模型图：

实践表明有部分学生看到了这种式子全是字母的题就会产生心理负担，而利用田字模型算法计算后就不再害怕了，并能轻松、准确地计算，但一定要弄清楚同类项的系数是什么，特别是含字母的系数的项。变式练习2：

（1）若（y-3）（y+8） =y+ay+b，则ab的值为

（2）已知（m+n-3）（m+n+3）=280，求m+ n的值.

分析：第（1）题与例2的解法相同，轻松算出y↵+5y -24=y +ay+b，得出a=5，b=-24;得出结果ab=-120。

让学生尝试应用田字模型算法计算第（2）题。方法1：直接用田字模型算法计算两个多项式的积，再用完全平方公式求出最后結果。

田字模型图：

方法2：观察等式得出第（2）题已知等式中两个多项式中有相同式子m+n，可以把m+n看作一个整体或一个项，再应用田字模型算法计算得出结论，从而求出这m+n的值。完整解答过程如下：

解：由（m+n-3）（m+n+3） =280得： （m+n）2-9=280

".（m+n）'=289

田字模型图：

把例2进行变式得一组练习让学生体验考查知识的形式虽变，但模型核心计算方法不变，所谓万变不离其法。变式第（2）题在乘法公式的基础上用整体代入方法解答，可以提升学生的思维能力。

（三）拓展应用田字模型算法锤炼数学思想

例3已知（x？+ax+8）与（x？-3x+b）的积中不含x和x项，求a与b的值。

思路分析：审题可知要求a与6的值，需知两个多项式的积，再结合题意“积中不含x和x项”可得与a、b相关的等式，从而得出结论。解答此题有两个关键之处：①计算（x？+ax+8）与（x？-3x+b）的积;②理解关键词“积中不含x和项”的含义是指积中含x和x3项的系数分别等于0.

田字模型图：

变式练习3：

（1）若（y+m）与（5y+1）的积中含y的一次项系数为3，则m=

（2）已知（x+mx+n）（x-3x+4）的展开式中不含x和x项，

求：①m与n的值;

②在①的条件下（m+n）（m'-mn+n）的值。思路分析：变式练习中第（1）题解题关键：一是计算积;二是找出“积中含y的一次项系数”，使之等于3即可求出m的值。第（2）题与例3类似，可仿照例3来解答，但一定要理解题中关键词语的含义。

例题和练习中多项式的项数从两项增加到三项，再次体验运用模型计算可化繁为简的效果。

多项式乘多项式的计算中，特别是三项式乘三项式的计算简直是相当部分学生的“恶梦”。通过田字模型算法的学习，终于从复杂的计算中解脱了，运用田字模型算法能清晰地有条理地计算出多项式乘多项式的积，极大限度的避免出错，从此爱上计算了，在收获的知识的同时也感受到成功的喜悦。设计例题及变式练习时注重了对学生的数学思想进行培养，如解答过程应用整体代换，数形结合的及转化等数学思想，以达到全方面提升学生的分析、计算能力和思维能力。

【参考文献】

【1】张思明著：《理解数学：中学数学建模课程的实践案例与探索》福建教育出版社2011年版，第46～48、206～207页。

【2】全国数学建模工作委员会著：《初中生数学建模能力培养教程》，济南出版社2014年版，第103～105页。

【3】张志存：《例谈方程思想在解题中是应用》，《中国教育与教学》2006年10月第4卷第8期。

【4】全国数学建模工作委员会：《初中生数学建模能力培养教程》（初一下册）。