高中数学少教多学教学模式下的前置研究设计

姜世仙

摘要：目前大多数学课堂都是老师讲，学生听，学生练得少，教学效果差。笔者经过探索发现如果课前设置好前置研究，就可以实现“少教多学”，而且教学效果显著。本文就前置研究的概念、原则以及高中数学常见课型前置研究的设计提出一些看法。

关键词：高中数学;前置研究;少教多学

高中数学课程要以学生发展为本，落实立德树人的根本任务，培育科学精神和创新意识，提升数学学科核心素养。反观现在的高中数学课堂，基本都是：概念、定理的形成一例题讲解一课堂练习三步骤，前两部分几乎是教师在讲，到练习这一块才留给学生的空间和时间，课堂也接近尾声了。从教学效果来看，学生在做当堂练习时基本能做出来，而过两周后多数学生完全不知所云，根本原因在于学生对数学概念、定理的构建没有自己的认知过程，被动的接受老师所讲内容，当堂练习时对比例题简单的重复、模仿，数学学科核心素养的提升、创新意识更是无从谈起。如何改变这一现状，笔者探索“基于前置研究的少教多学的三学课堂教学模式”，而前置研究是少教多学、先学后教的基石，对课堂教学起着举足轻重的作用。

一、前置研究及其原则

前置研究，又称为前置性小研究或前置性学习，是以生本教育理念为先导的一种教学方式。教师将下一节课要学习的内容以简单、根本、开放的形式布置成各种小研究，让学生根据自己的知识水平和生活经验进行尝试性学习，是指导学生先学的重要方案，为新课学习做准备、铺垫、指引。前置研究的设计以学生好学为原则，以让学生能学为前提，学生围绕前置研究能自主解决50%以上问题，并标注出疑难问题。前置研究必须遵循简单、根本、开放的原则，从源头上把学习的权利还给学生。

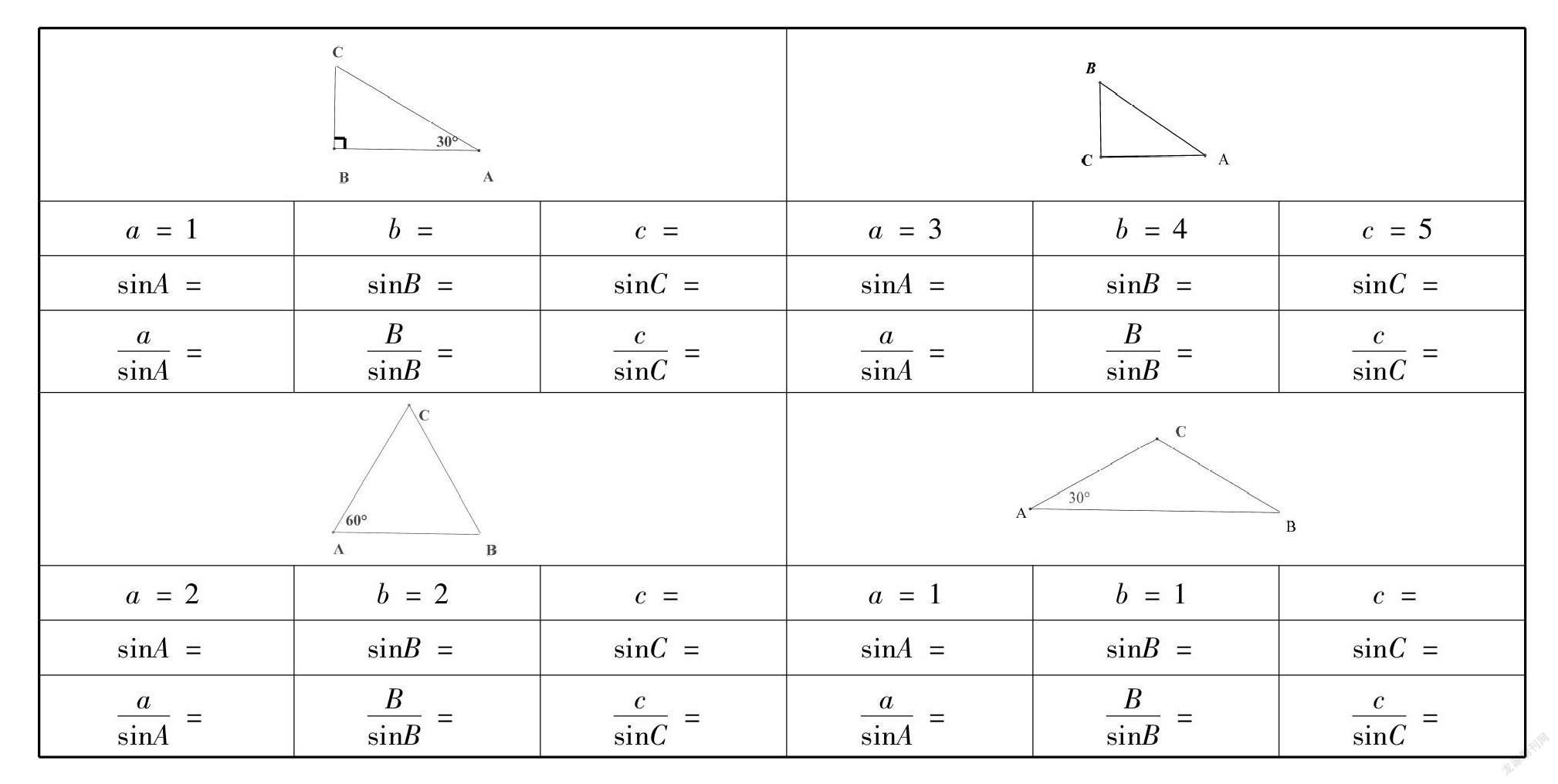
简单有两重含义：一是容易，二是大道至简。只有把知识变得容易了，学生才好（hdo）学。刚开始我在摸索前置研究的设计时在想：如果不确定自己做的前置是否遵循了简单原则，可以找两个班里数学基础较弱的学生先来做一做，如果他们做不出来，就要更改，更改好了才能布置给全班学生做。以必修五《正弦定理》前置研究为例，前置研究必须遵循简单原则。

（1）在OABC中，LA、LB、LC所对的边分别记为a、b、c;在以下4个三角形中，请同学们完成相应表格：

规律总结：由以上数据，同学们能得出什么结论？（2）同学们能证明此结论吗？请结合必修五教材第2～3页，尝试给出证明。

根本在这里是指事物的根源、基础、最重要的部分。很多的知识、方法是由“根”长出来的，这里“根”就是知识生长的地方和方法形成的地方，更是思维发生的地方，在备任何一节课时，都必须先想清楚本节课的根是什么，只有牢牢地抓住了根，才能抓住问题的本质。

开放在这里有两重含义，一是对不同层次的学生的要求是不同的，即对学生的要求是开放的;二是问题的设计是开放的，问题的解决方案或答案是多样的。开放了，学生有信心完成前置研究，开放了，学生上课有话可说，有话题可以辩论。例如《求数列{n.x"-|}的前n项和》的前置研究的设计主要是三个环节：①不用公式，请同学们求数列{x"}的前n项和;②你能类比上一题的方法求数列{n.x}的前n项和吗③请同学们以学习小组为单位找一个类似的数列，并求出它的前n项和。不能用公式求数列{x～一}的前n项和，倒逼同学们回顾、查找等比数列前n项和公式的推导，再利用类比的思想方法推广利用错位相减的方法求差比数列的前n项和;最后一个环节的设计，完全彰显出了前置研究的开放原则，各小组的同学积極准备、探索，给出了如{（2n-1）.x"|}、{n.2"}、【2n+l】.【1-2n】等数列的前n项和的求解。多次 2” 」l3n-1

施教发现：学生的潜力是无限的，公差是负数的题目都涉及了，要给他们充分发挥的时间和空间。

二、高中数学常见课型前置研究的设计1.新授课前置研究设计。

新授课的内容是学生从无到有的过程，如何让学生更好探索新知识？前置研究的先学后教、先做后学起到很好的奠基作用。作为一线的数学教师，我们要认真研读高中新课程标准，明确课标对每堂课教学内容的要求，找准重点、难点。前置研究的内容要充分体现下一堂课教学重点，或是对重点内容的抛砖引玉，同时结合本班学生已有的认知水平。通过前置研究的个人独学，学生对新课内容做到心中有数，知道自己能解决的问题及存在疑惑的地方，并做好标记，为课堂小组对学及班级群学做铺垫。以下以必修二《直线与平面所成角第一课时》为例：

（1）观察你和同桌的握笔情况，你们写字时笔所在直线与纸面的倾斜程度是否一样？有何不同？

（2）动手操作：将一支笔斜插在桌面上，另一支放在桌面内，请找出两支笔所在直线所成角;移动平面内的笔，观察两支笔所在直线所成角，哪个角可以用来表示笔所在直线与纸面的倾斜程度？

（3）阅读必修二教材第66页，指出斜线与平面所成角的定义。

（4）结合下图，在图上指出斜线、斜足、垂线、 垂足、斜线在平面内的摄影、斜线与平面所成角。

（5）当直线与平面平行或直线在平面内时，直线与平面所成角是___________

当直线与平面垂直时，直线与平面所成角是___________

斜线与平面所成角范围是___________

所以，直线与平面所成角范围是___________

课前的前置学习学生通过观察、动手操作等过程，学生体会到数学源于生活，在整堂课教学中，教师引导学生紧紧抓住根：斜线、垂线、射影。

2.习题、章节复习课前置研究设计。

习题、章节复习课是在学生学习知识后进行的，学生已具备相应的基本知识。故此类课型前置研究应包括：①三基整理：基本概念（定义、公式、概念）、基本技能、基本方法;②典型例题;③方法总结提升。课堂上请小组代表展示讲解，对于三基部分，同学们可补充、质疑，教师协助找出核心部分。例题展示讲解部分要注意引导、提问，规范答题过程，数学基本思想方法的总结、升华。如果是毕业班则可以根据每个小组的情况适当增加题目来提高梯度。复习课中，学习小结一定要让学生用自己的语言总结并讲出来与大家分享，而且在课堂上一定要完成好这个环节，老师引导补充，这样就可以让学生更好地理解一节课的内容。

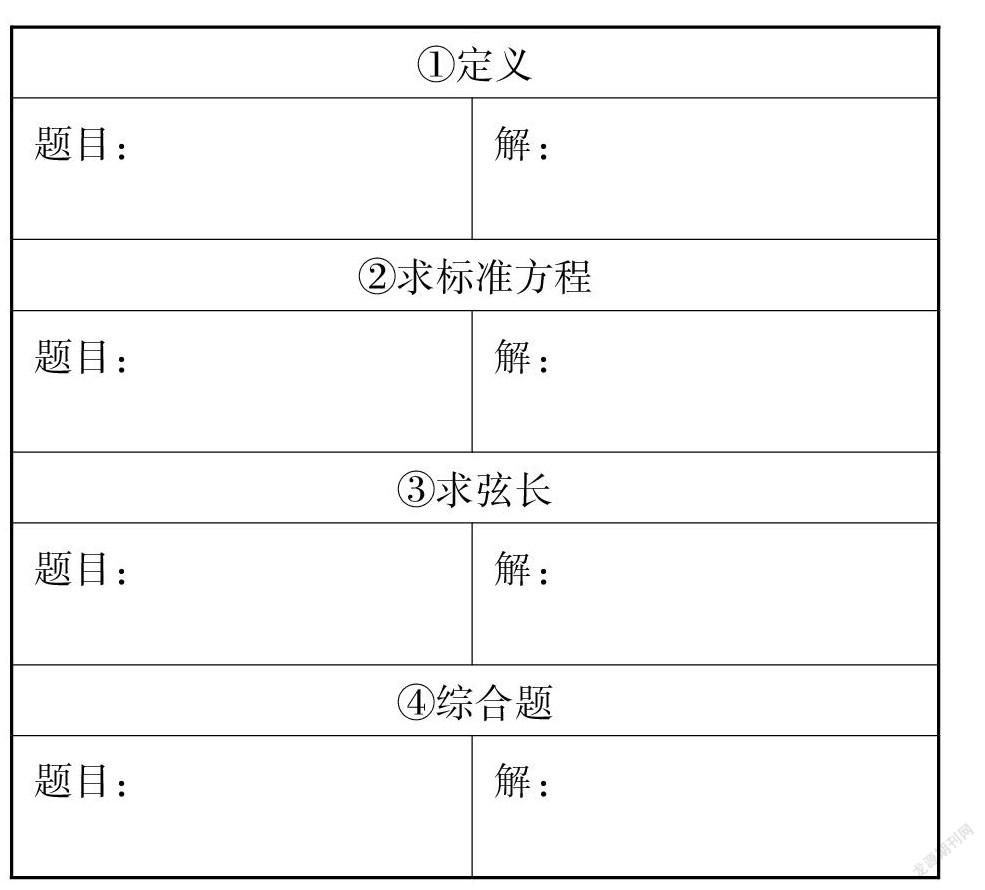
三、抛物线标准方程及其性质习题课前置探究

1.三基整理。

（1）定义。

（2）抛物线的标准方程及几何性质

（3）解决直线与抛物线相交问题的通法：

（4）对以上的基础知识你有没有需要补充的？如有，请写出来。

2.例题：请同学们根据下列对应知识点各找一道题，并做好小组交流的准备。

请同学们通过前置学习做小结，你有什么收获？学习小结：

课堂小结：

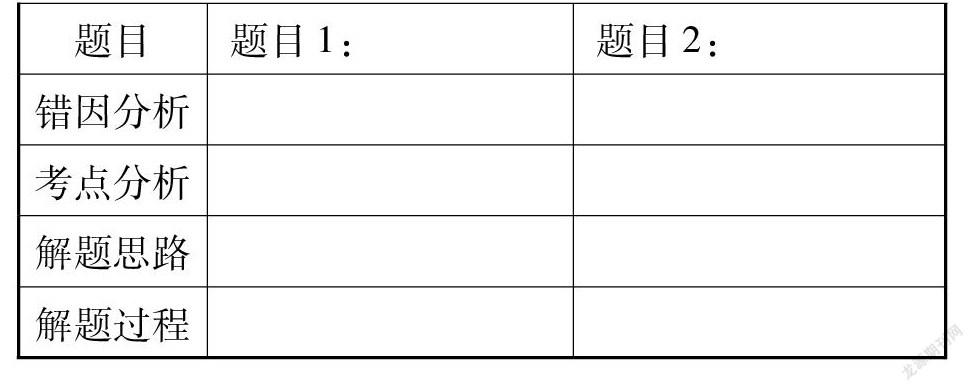
3.试卷讲评课前置研究设计。

考试是对学生一段时间学习成果的检测，我们重视的不止是考试成绩，还有考试结束后对试卷的分析、订正。考试结束后学生先订正，发现自己学习中存在的问题，包括相关知识的掌握、解题思路的分析、答题的规范等等。不会改正的题目请教同学、老师，学生要先总结、反思，然后再讲评，讲评以学生讲解、展示为主，教师对学生讲解总结不到位的及时进行补充。

（1）请自行订正期中考试试卷，做错的题目重新做一遍，如不会，请请教其他同学。

（2）请选择两道你做错的题，写好解题过程，并做好小组交流的准备！

（3）请自己找一道类似错题的题型，你是否完全掌握？

题目：

解答：

经过两年多的探索和实践，笔者在前置研究的设计方面取得了显著的进步，常常与备课组同事一起精心设计前置研究，不论是新授课还是复习课，大家都能设计出合理的前置学习，为少教多学、先学后教奠定坚实的基础。

很多学生高中阶段最怕的学科就是数学，自己很想把它学懂、学好，每节课一开始自己都认真听老师讲，但不知道从哪个点开始，自己只能看到数学老師的嘴一张一合，而大脑一片空白，完全不知道老师在说什么了。对于基础本身就较薄弱的学生，很多女同学一开始就对数学有畏惧心理，但是可以放弃数学不学吗？答案是否定的，学生学习从基于前置研究的个人独学到小组结伴研讨的团队学习，在数学课堂上，学生获得了充分的学习体验。设置好合理的前置研究，组建好学习小组，课堂上推进好我校开展的“三学课堂”教学模式，还课堂于学生，我们在探索中实践，在实践中不断进步，实现人人都能获得良好的数学教育，不同的人在数学上得到不同的发展。

【参考文献

【1】齐艳霞：《高中数学课堂教学中的少教多学模式研究——画出y=Asin（wx+q）在给定区间上的图象的教学案例与评析》，《教育教学论谈》2013年。

【2】田维康：《初中数学教学中“少教多学”模式之的运用》，《数学学习与研究》2018年。

【3】王娟：《咬定“生本”不放松“前置研究”在其中》，《小学教学研究》2018年。

【4】马颖：《如何提高“前置性小研究”的研究价值》，《甘肃教育》2018年。

【5】王盛建：《前置性学习在模具结构教学中的应用》，《职业》2014年第11期。

【本文是广州市教育科学“十三五”规划2019年度一般课题《基于前置研究的高中数学少教多学教学模式探索》（课题编号：201911964）阶段性成果】