提升思维能力 发展核心素养
2020-12-06尹冉肖艳
尹冉 肖艳
思维能力是数学学科核心素养的关键能力,本文结合《图形的运动(旋转)》的学、教过程,引导学生学会数学思考、提升思维能力,在数学课堂上落实核心素养的培养。
一、暴露误区,找准思维方向
在引入环节,教师先通过小魔术引出红色小棒(小红),并用课件演示小棒在跑道上平移、在单杠上旋转的现象,引导学生思考并回答在数学上这样的运动分别叫“平移”和“旋转”;再出示“荡秋千”和“钟摆的运动”两种运动现象,请学生思考“它们是否属于旋转,为什么”。一部分学生认为不属于旋转,因为它们只是轻微摆动,并没有转到一圈;另一部分学生认为是旋转,因为它们虽然没有旋转到一圈,但这只是它们旋转角度的大小问题,并不能说它们不是旋转。此时,教师明确提出:物体只要绕着一个点或一个轴转动,不管有没有转一圈,都属于旋转,所以,荡秋千和钟摆的运动都属于旋转。
本课从生活中的“平移”和“旋转”现象入手,教师积极唤醒学生以往所积累的图形运动的相关知识与经验,帮助学生确立认知根基。用“它们属于旋转吗”的问题,暴露学生思维上“旋转要转一圈”的误区,引发认知冲突,使学生通过思维碰撞消除知识漏洞,为新课的开展做好铺垫,找准思维方向。
二、建构认知冲突,唤醒思维活力
恰当的问题情境有助于学生感受数学知识在现实生活中的应用价值,唤醒学生的思维活力。在教学时,教师应在深入剖析教材的前提下,创设有趣的、贴近学生生活的情境,调动学生的积极性。
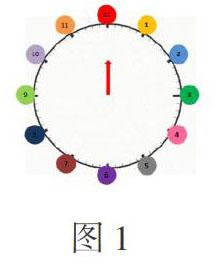
教师用课件出示打气球游戏情境(如图1),请学生尝试为发射器编辑旋转指令,试打3号气球。
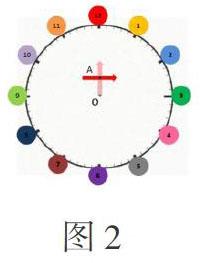
有学生回答“发射器向右旋转90度”,还有学生回答“发射器按顺时针方向旋转90度”。教师引导学生思考:如果把“按顺时针方向旋转90度”的指令下达给发射器,能瞄准3号气球吗?学生往往信心满满地回答“能!”教师利用课件演示(如图2)后,学生陷入认知冲突。教师借此引发学生思考并感悟到:要想准确地描述旋转,还必须描述清楚旋转的“点”,即“旋转中心”。随后,教师请学生修正自己的旋转指令为:“发射器绕点O按顺时针旋转90度”,课件演示成功击中3号气球。
教师通过对比学生的旋转指令,构建认知冲突,引导学生在自主尝试中逐步感悟到:要想描述清楚发射器的旋转,必须准确把握“旋转的中心、方向、角度”,即旋转三要素。精心设计的探究活动,激活了学生的思维,让他们变被动接受为主动思考,在一次次认知冲突中真正领悟到旋转三要素的必要性。
三、巧设活动,提升思维层次
苏霍姆林斯基曾说:“学生的智慧在他的指尖上。”好的数学活动不仅有利于突破教学难点,更是引发学生高阶思维的重要途径。教师设计有梯度的教学活动,有助于推动学生思维向更高层次发展。
師:请你选择一个喜欢的气球,给发射器编辑一道旋转指令,让它瞄准你心里想的那个气球。(学生编写指令)现在我们来玩猜一猜的游戏。先请一位同学说指令,另一位同学猜他想瞄准哪个气球。
生1:发射器绕点O按顺时针方向旋转60度。
生2:5号气球。
师:再请一位同学说说想瞄准哪个气球?另一位同学来猜旋转指令。
生3:6号。
生4:发射器绕点O按顺时针方向旋转90度。
师:有没有不同的指令也能达到同样的效果?
生5:发射器绕点O按逆时针方向旋转270度!
“猜一猜”的游戏活动,一方面巩固了学生运用旋转三要素描述旋转运动的能力;另一方面通过“先说指令猜气球,再说气球猜指令,最后思考能达到同样效果的不同指令”这样有梯度的设计,促使学生的思维不断深入,思维层次得到有效提升。
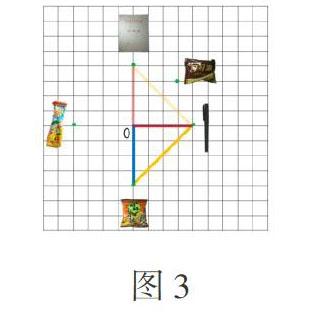
在操作感知旋转特征的环节,教师设计了用三根小棒(小红、小蓝、小黄)围成三角形进行旋转的游戏(如图3)。
师:如果想让小红指着棒棒糖,三角形要如何运动呢?请各组拿出三角尺和抽奖卡试着转一转。通过操作,你发现小红和小蓝的运动有何关联?
生1:小红和小蓝的旋转中心、方向、角度相同。
师:这就是图形旋转的特征。旋转中心不变,过旋转中心的每条边的旋转方向和旋转角度都相同。如果你来抽奖,有可能同时得到哪些奖品?能同时得到可可派和小小酥吗?为什么?(以小组为单位操作讨论后请代表汇报演示。)
生2:有可能同时得到练习本和笔、笔和小小酥、小小酥和棒棒糖,还有棒棒糖和练习本。不管三角尺如何旋转都不可能同时得到可可派和小小酥。
师:谁能用数学知识解释一下原因?
生3:因为小红和小蓝的夹角是90度,而可可派和小小酥之间的夹角大于90度。
师:在旋转后,三角形的形状和夹角大小不变。三角形的什么变了?
生4:位置变了。
教师通过精心设计的“问题串”,引导学生自主探索,循序渐进地促使学生深度参与、深度思考,达成深度理解,丰富并发展了学生的基本活动经验。
四、拓展延伸,挖掘思维深度
在教学中,教师应在充分研读教材和学情的基础上,抓住知识节点适时拓展延伸,为学生的深入思考提供可能,进而挖掘学生的思维深度。?
师:今天这节课,三角形始终是绕着点O在旋转,请思考三角形还能以哪里为中心旋转?
生1:还能绕着点A和点B旋转。
师:三角形除了可以绕着它的3个顶点旋转,还能以哪为旋转中心?
生2:还可以绕着边上的任意一点旋转。
师:还能以哪里为旋转中心?
生3:三角形内部的任意一点!
师:你太有想法了!受他的启发,还有吗?
生4:还能绕着三角形外部的任意一点旋转!
师:这些是三角形绕着一个点旋转而形成的美丽图形(课件展示)。除了能以一个点为旋转中心,还能以哪里为旋转中心呢?
生5:还能绕着它的一条边旋转!
师:你的想法太有创意了!
从线段(发射器)的旋转,到图形(三角形)的旋转,是一个循序渐进、层层递进的过程。但图形的旋转并不止步于此,本环节尝试用启发性问题引导学生突破思维“禁锢”,同时发展了学生的空间观念。
五、回归生活,拓宽思维广度
课堂最后,以视频资料展示旋转在体育、艺术、科技等方面的应用,通过观赏这些真实而震撼的画面,使学生的思维广度得到有效拓展,感受到数学与生活的紧密联系。
(作者单位:尹冉,襄阳市第二十中学;肖艳,襄阳市樊城区教研室)
见习编辑 刘佳
