一类具有记忆项的耦合梁方程的全局吸引子

高慧芳

（朔州师范高等专科学校数计系，山西朔州 036000）

1 引言

吸引子是无穷维动力系统中的一个重要概念，常用来衡量解的长时间行为，因此研究吸引子有着很重要的意义.文献[1，2]研究了不同边界条件下梁方程的整体吸引子，对梁方程其他吸引子的研究可见文献[3-5].之后人们对有记忆项的耦合梁方程又做了进一步的研究，文献[6，7]讨论了耦合梁方程的整体吸引子，文献[8，9]讨论了具有记忆项耦合梁方程的一致吸引子和整体吸引子.

文献[3]研究了非线性耦合梁方程：

Ω为Rn的一个有界光滑区域，n=1或2.

本文在文献[3]的基础上取n=1的情况考虑以下耦合梁方程：

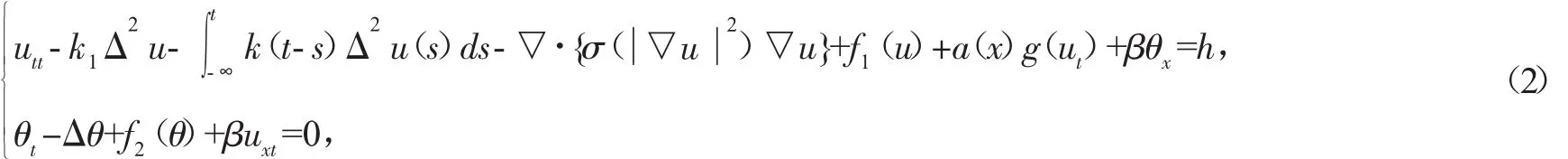
边界条件：

初始条件：

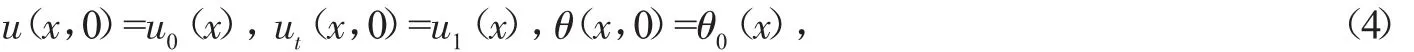
其中 Ω=[0，L]为 R 上的一个有界光滑区域，σ（v）∈Cm+2（[0，L]），a（x）∈Cm-1（Ω）是上的非负光滑函数[1，3].

2 预备知识

首先作如下假设[2]：

（H1）对于 μ∈C1（R+）∩L1（R+）有

3 全局吸引子

初始条件：

由引理2得半群S（t）在H是渐近紧的.

综合定理2和3得C0-半群{S（t）}t≥0在H中存在全局吸引子.