算子几何-算术平均值不等式的推广
2020-12-05宋园
怀化学院学报 2020年5期
宋 园
(滁州职业技术学院,安徽滁州 239000)
1 引言
用B(H)表示可分Hilbert空间H上所有线性算子生成的代数.设自伴算子A∈B(H),如果对于任意给定的x∈H,都有(Ax,x)≥0,则 A 称为是正的.设 A,B∈B(H)且 A,B 为自伴算子,B-A≥0表示 B-A 为正算子,记为B≥A,BA>0表示B-A为可逆正算子,记为B>A.
设A,B为可逆正算子,定义A,B的几何均值A#B和相对算子熵为S(A|B)分别为[1-3]:
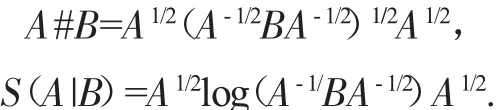
设 a,b>0,众所周知,有
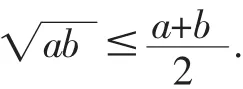
这是著名的几何-算术平均值不等式.这个不等式在有界线性算子所组成的非交换代数上的形式如下[3]:设A,B为可逆正算子,则

最近,Zou和Jiang在文献[4]中得到了不等式(1)的一个改进:

其中
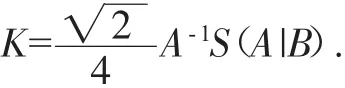
关于不等式(2)的一些应用和变形可参见文献[5,6].本文将给出不等式(2)的一个推广.
2 主要结果
这里将给出本文的主要结果及其证明过程,为了得到结果,需要如下的引理.
引理 2.1[7]设 a,b>0,当 0≤x≤1 时,


对于一般的正算子B,可令B=B+εI,重复上面的过程,然后再令ε趋于零.这就完成了证明.
注2.1 假设A为可逆正算子,令C=A1/2,由定理2.2可得不等式(2),所以定理2.2是不等式(2)的一个推广.
