一类扰动五次哈密顿系统的双尖点极限环
2020-12-05洪晓春杨春妮
洪晓春,张 伟,杨春妮
(1.云南财经大学 统计与数学学院,昆明 650221;2.新东方学校 西安市雁塔区培训中心,西安 710000)
对于希尔伯特第16问题,平面多项式向量场极限环的个数及分布问题得到了广泛研究,获得了大量优秀成果.为了解决这个难题,V.I.Aronld提出了弱化的希尔伯特第16问题[1],即扰动系统的Abel积分零点个数上界与极限环个数的关系问题.
(1)
其中a,b,c∈R且c≠0.
系统(1)是一个超椭圆哈密顿系统,文献[2]证明了系统(1)在(a0+a1x+a2x2)y,ai∈R(i=0,1,2)扰动下的极限环个数不超过3个.文献[3]证明了系统(1)在任意n次多项式扰动下的极限环个数不超过5n-3.
(2)
文献[4]应用判定函数方法和数值模拟方法[5]给出了系统(2)有3个极限环.
(3)
文献[6]应用判定函数方法和数值模拟方法给出了系统(3)有3个极限环.
(4)
文献[7]应用判定函数方法和数值模拟方法给出了系统(4)有3个极限环.
(5)
其中R(x,y,λ)=mx2+ny2+ky4-λ.文献[8]应用判定函数方法和数值模拟方法给出了系统(5)有15个极限环.
(6)
(7)
其中R(x,y,λ)=mx2+ny2+kx2y2-λ.文献[9]应用判定函数方法和数值模拟方法给出了系统(6)及系统(7)均有8个极限环.
(8)
文献[10]对系统(8)的相图情况进行了分类,分为a,b,c,d,e,f,g7种情况,并且证明了系统(8)在任意n次多项式扰动下的极限环个数不超过54n-13.

(9)
其中q(x,y)=a0+a1x2+a2y2,ai∈R(i=0,1,2),0<ε≪1.
应用判定函数和数值计算方法,得出系统(9)有3个极限环,而且出现双尖点极限环的情况.当a1=-1,a2=0.95,ε=0.001时,分别取a0=-0.02,a0=-0.041 145 8,a0=-0.06,使用数值模拟方法[11]给出了3个极限环的具体位置.
1 对非扰动系统的分析
(10)
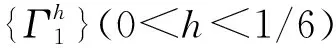
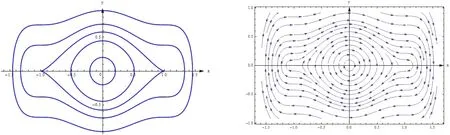
图1 非扰动系统(10)的相图Fig.1 Phase diagram of the unperturbed system (10)
(11)
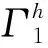
(12)
当y=0时,由式(11)可得:
x6-3x4+3x2-6h=0.
(13)
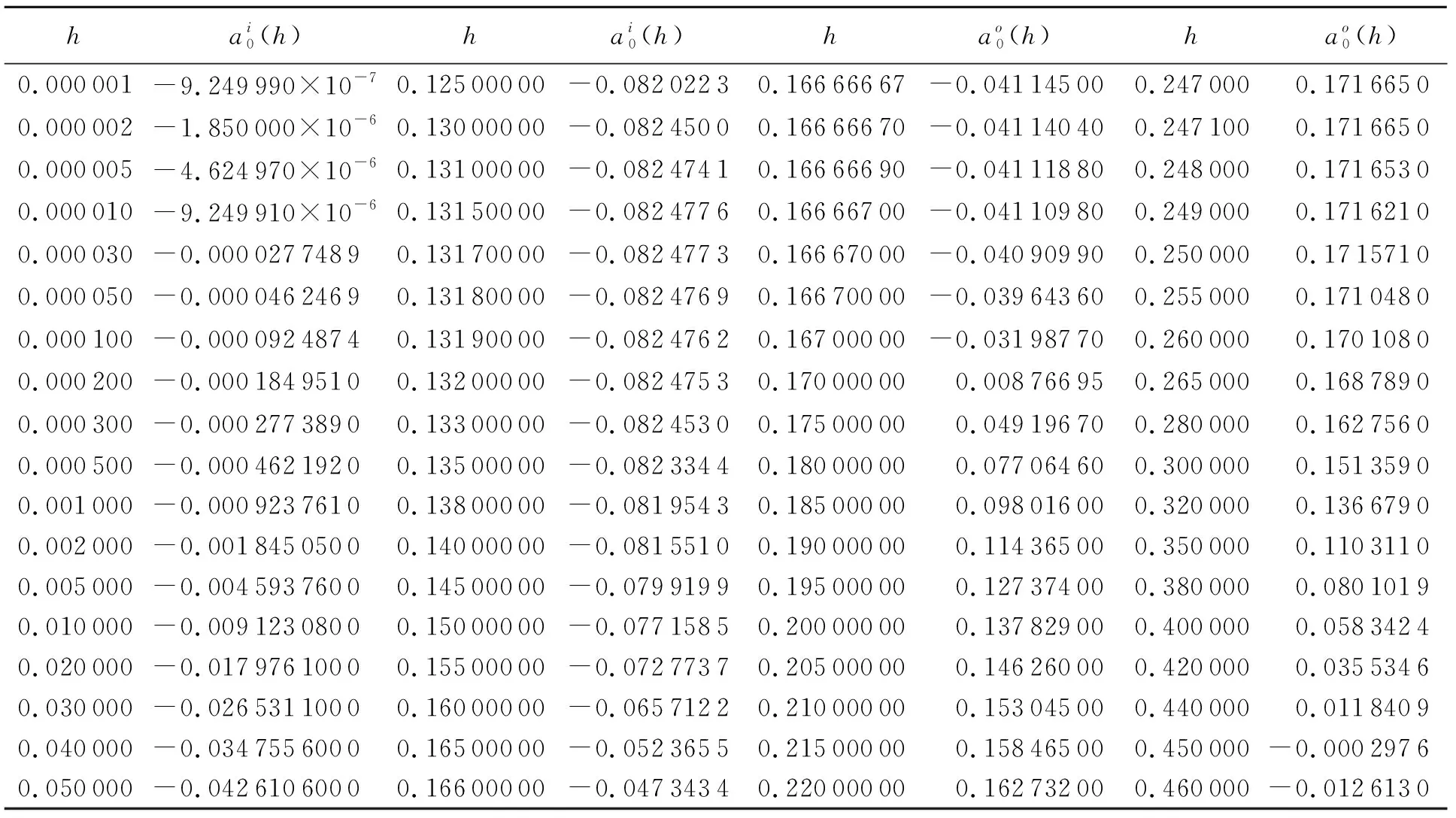
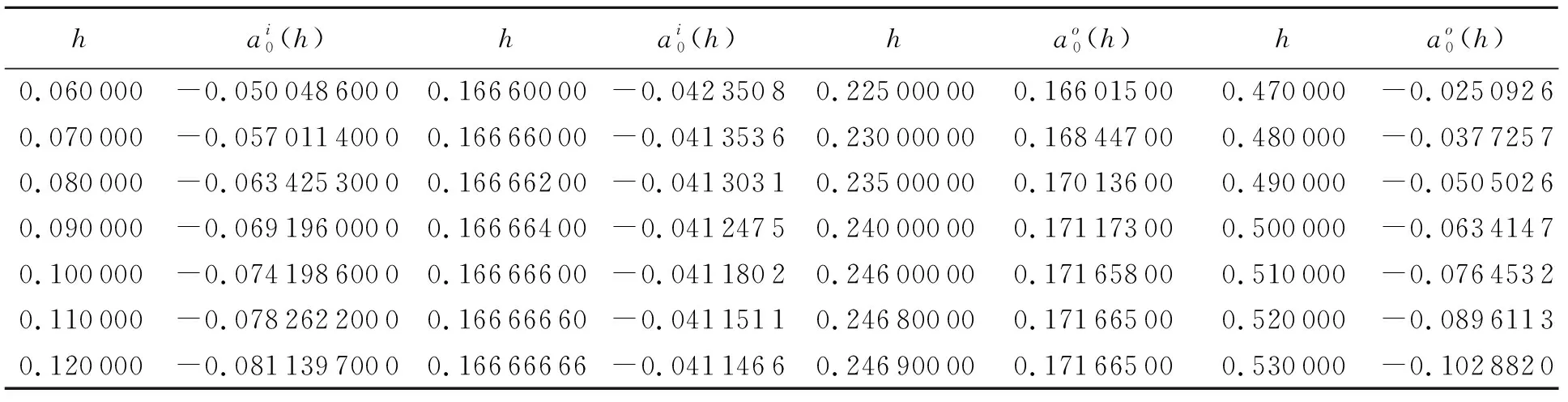
对于任意的h(0 文献[5]中研究了如下扰动系统: (14) 其中p(0,0)=q(0,0)=0.令Abel积分A(h)=0,得到: (15) (16) 则函数λ(h)称为扰动系统(14)的判定函数. 定理1[5]对于任意给定的λ0, 1) 如果(h0,λ(h0))是直线λ=λ0与判定曲线λ=λ(h)的交点,且λ′(h0)>0(<0),系统(14)在Γh0附近当λ=λ0时有一个稳定(不稳定)的极限环. 2) 如果直线λ=λ0与判定曲线λ=λ(h)没有交点,则系统(14)当λ=λ0时没有极限环. 同理,如果随着h的增加,Γh向内收缩,极限环的稳定性与之相反. 为了简洁,此处略去定理的证明. 图2 当a1=-1,a2=0.95时,扰动系统(9)的判定曲线Fig.2 Detection curves of the perturbed system (9) when a1=-1 and a2=0.95 对于扰动系统(9),可得其Abel积分:A(h)=∮Γh(a0+a1x2+a2y2)ydx. (17) 对式(17)使用格林公式得: A(h)=-∬Γh(D)(a0+a1x2+3a2y2)dxdy. (18) 令A(h)=0,由式(12)、(13)、(18),可得两个判定函数如下: (0 (19) (1/6 (20) 当a1=-1,a2=0.95时,由式(12)、(13)、(19)、(20),可得判定函数如表1所示. 由表1表示的函数,可以得到系统(9)的判定曲线,如图2所示. 表1 当a1=-1,a2=0.95时,扰动系统(9)的判定函数Tab.1 Detection functions of perturbed system (9) when a1=-1 and a2=0.95 续表1 由定理1及系统(9)的判定曲线(图2),可以得出以下定理. 定理2 对于系统(9),当a1=-1,a2=0.95,0<ε≪1时,由系统的判定曲线,可得到以下结果. 1) 当a0<-0.082 477 6或a0=0.171 66 5时,系统(9)有1个极限环. 2) 当0≤a0<0.171 665或a0=-0.082 477 6时,系统(9)有2个极限环. 3) 当-0.082 477 6 大、小极限环分别通过点(1.490,0)和(0.216,0),它们 都是不稳定的;中极限环通过点(1.087,0),它是稳定的图3 当a0=-0.02,a1=-1,a2=0.95,ε=0.001时,系统(9)的3个极限环及它们的位置Fig.3 The 3 limit cycles and their locations of system (9) when a0=-0.02,a1=-1,a2=0.95,ε=0.001 大、小极限环分别通过点(1.495,0)和(0.327,0),它们都是不稳定的;中极限环(双尖点极限环)通过点(1,0),它是稳定的图4 当a0=-0.041 145 8,a1=-1,a2=0.95,ε=0.001时,系统(9)的3个极限环和它们的位置Fig.4 The 3 limit cycles and their locations of system (9) when a0=-0.041 145 8,a1=-1,a2=0.95,and ε=0.001 大、小极限环分别通过点(1.503,0)和(0.423,0),它们都是不稳定的;中极限环通过点(0.842,0),它是稳定的图5 当a0=-0.06,a1=-1,a2=0.95,ε=0.001时,系统(9)的3个极限环和它们的位置Fig.5 The 3 limit cycles and their locations of system (9) when a0=-0.06,a1=-1,a2=0.95,ε=0.001 本文运用判定函数方法[5]给出了系统(9)的极限环分支情况.研究表明,在特殊三次扰动下,当a1=-1,a2=0.95,-0.082 477 62 判定函数和判定曲线
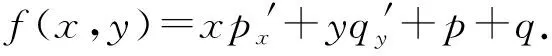
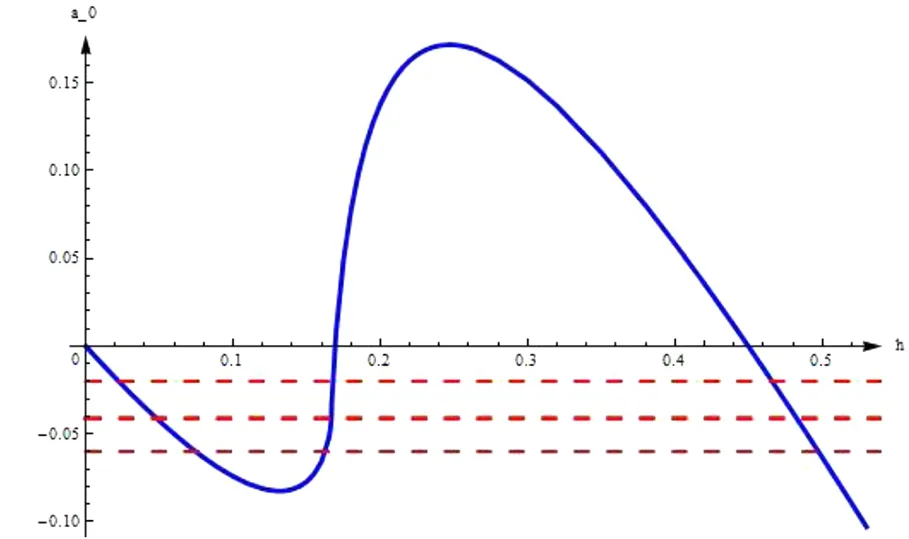
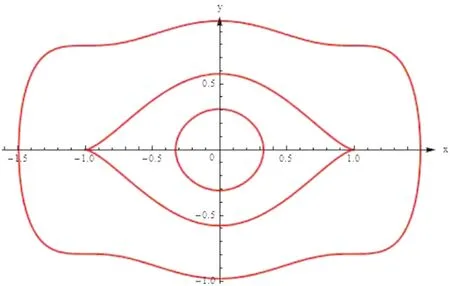
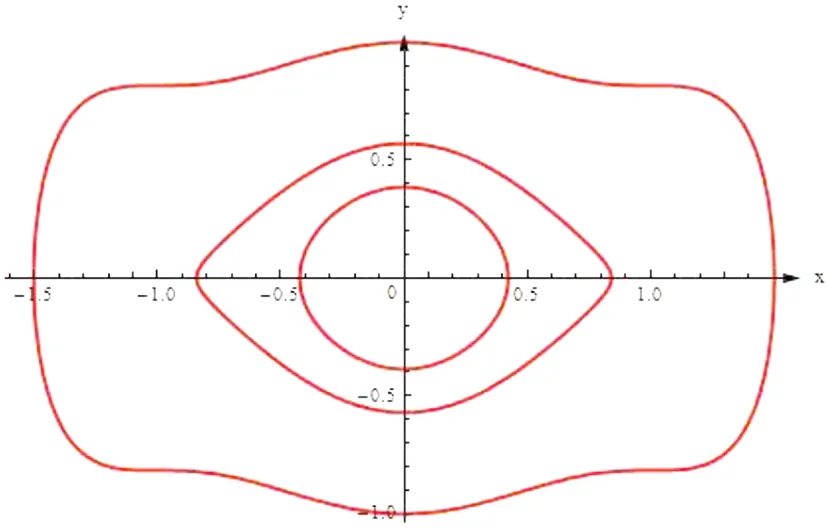
3 扰动系统(9)的极限环分支
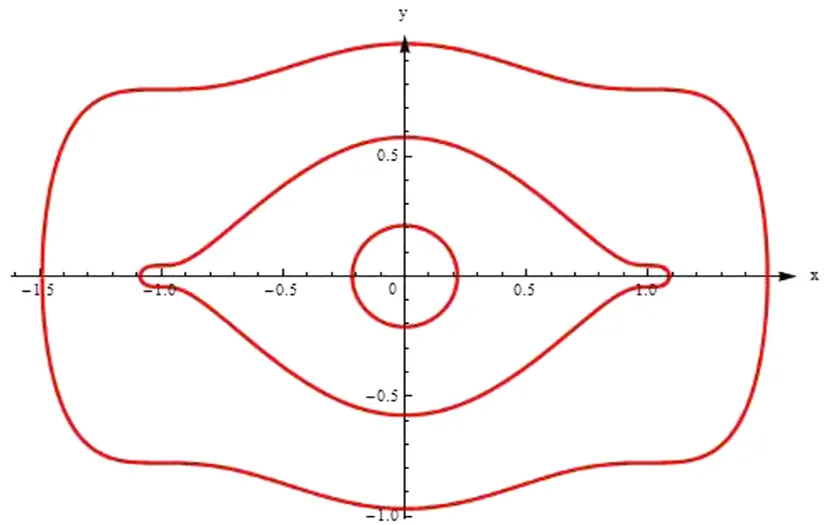
4 结语
