基于土壤水分实测数据的土壤线提取
2020-12-05周亚楠董张玉
方 帅, 周亚楠, 董张玉
(1.合肥工业大学 计算机与信息学院,安徽 合肥 230601; 2.工业安全与应急技术安徽省重点实验室,安徽 合肥 230601)
土壤线是描述裸露土壤在近红外(near infrarea,NIR)波段反射率NIRmin与红波段反射率R之间线性关系的重要概念[1],它能较好地描述土壤的光学特征,有助于了解土壤和植被的理化性质和生态特征,许多常用的植被指数和干旱指数都借助了这一概念。目前对土壤线的提取,传统的方法是基于地面实测的土壤光谱数据进行土壤线的计算,如文献[2]利用室内测定的土壤光谱反射率计算土壤线,并将其用于与土壤线有关的植被指数的计算,再利用植被指数结果验证土壤线计算方法的可行性。传统的方法虽然精度高,但是获取数据相对复杂,因此越来越多的学者将研究重点转向从遥感影像中直接提取土壤线。文献[3]从遥感图像分类提取山东典型土壤的裸土信息,并计算不同土壤类型的土壤线;文献[4]基于裸土点在NIR-Red特征空间中常分布在三角区域下方的特征,提取裸土点并拟合土壤线;文献[5]采用自适应区间选取对土壤点进行初步筛选,随后利用循环迭代剔除非裸土像元。以上3种算法都需要足够量的裸土像元,这在实际中是难以满足的。文献[6]在提取加拿大混合草地的土壤线时采用分位数回归法和(R,NIRmin)法,并发现2种方法在植被生长早期和衰老期提取的土壤线都比较好,在植被生长期(R, NIRmin)法提取结果更好;而在植被成熟期,由于土壤被植被覆盖而导致裸土像元很少,因此2种方法提取结果均不理想。文献[7]提出利用5条不同土壤类型土壤线的平均值来降低土壤线位置的不确定性,并在后续研究[8-10]中均使用了统一的土壤线参数;该方法虽然普适性较好,但由于影响土壤线的因素[3,11]较多,采取统一的土壤线代替实际土壤线势必会造成较大的误差,而且该方法同样需要足够的裸土像元。
NIR-Red特征空间下提出的改进的垂直干旱指数(modified perpendicular drought index,MPDI)模型中,MDPI是用来表征土壤含水量的一种指数,它是通过土壤线参数计算得到的。因此,从本质上来说,土壤线的精度会严重影响土壤水含量的估计。遥感图像提取土壤线需要的足够裸土像元是很难保证的,这是由于不同地区、不同季节植被覆盖情况以及遥感图像空间分辨率的限制。针对此问题,考虑到土壤线求解的不准确会导致土壤水含量计算误差,本文利用这一误差反馈来修正土壤线,从而克服因纯裸土像元点缺乏而导致土壤线拟合结果不准确的问题。
各类文献中常利用水含量估计精度评价土壤线算法的性能[5],本文则是利用估计土壤水含量与实测土壤水含量的误差修正土壤线的估计。本文基于土壤线模型构造目标函数数据项,利用水含量估计误差构造目标函数正则项,在一个目标函数下迭代交叉估计土壤线和水含量;利用水含量的误差修正土壤线,更加精确的土壤线再来提高水含量的估计精度。在交叉迭代过程中,土壤线和水含量估计精度都得到了提高。本文提出的交叉迭代框架同时也适用于其他地面实测数据相关的约束,可以进一步推广到土壤线与植被指数[12]的求取等。
1 数 据
1.1 研究区域和实测数据
澳大利亚作为世界上最干旱的国家之一,被选为本文的研究案例。从1990年开始,该国家的降雨量开始逐年低于平均水平。近几十年来,澳大利亚经历了几次严重的干旱[13-15]。
由于澳大利亚没有全面覆盖的土壤水分实测数据,本文选择位于澳洲新南威尔士西南部、区域平坦、森林植被相对较少的Yanco地区,该地区是马兰比季河土壤水分监测网络(Murrumbidgee soil moisture monitoring network, MSMMN)[16]的3个监测区域之一。MSMMN数据适合于遥感研究。文献[17]应用这些数据集来评估卫星预测的潜力;文献[18]利用这些数据提出了一个评估AMSR-E卫星土壤水分产品的框架;文献[19]利用MSMMN收集潜热通量数据,验证中分辨率成像光谱仪(moderate-resolutionimaging spectroradiometer,MODIS)衍生的蒸散量的产品。
本文研究的区域为澳大利亚Yanco区域,如图1所示,其中右上角显示了Yanco区域分布的37个站点。

图1 研究区域Yanco以及Yanco区域中的37个站点
本文使用的实测土壤水分数据为Yanco中MSMMN项目采集的现场数据,该测量数据由0~5、0~30、30~60、60~90 cm的平均土壤湿度和平均土壤温度组成。
1.2 卫星数据和图像预处理
本文选取Yanco地区2013年5月至2015年6月间9幅云量较少的Landsat8卫星图像,利用第4波段和第5波段的反射率构建NIR-Red特征空间。Yanco区域的Landsat8卫星影像和实测数据见表1所列,其中实测站点总数为226个。表1展示了本文使用的陆地卫星Landsat8图像信息以及对应站点的现场数据。其中,Landsat8 L1T产品已经经过几何修正,可以在网址http://earthexplorer.usgs.gov/下载获得;关于辐射校正,可以使用ENVI/FLAASH软件对近红外波段和红波段进行辐射校正;所需的大气校正参数可以从原始图像数据和最近的气象站收集到的数据中得到。
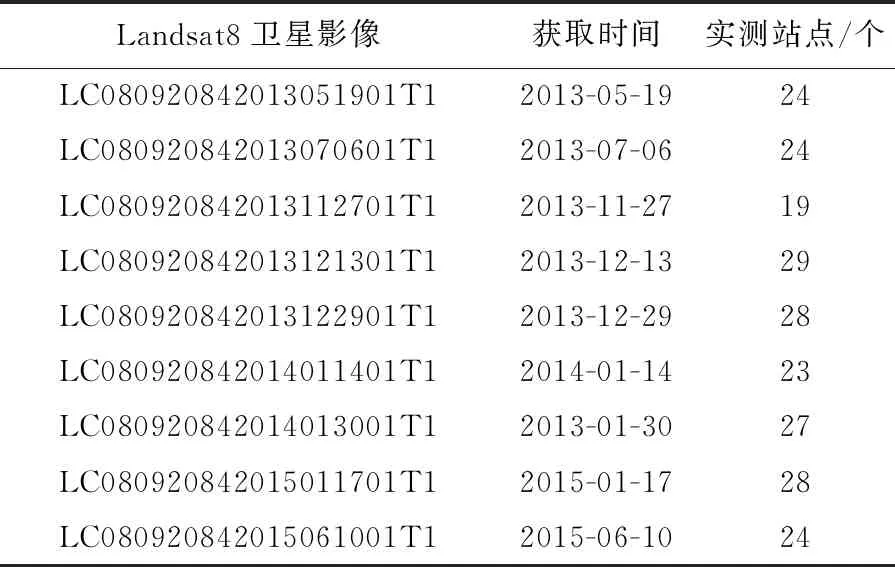
表1 Yanco区域的Landsat8卫星影像和实测数据
2 方法与模型
2.1 NIR-Red特征空间以及MPDI
当场景中包含土壤和植被时,在近红外波段和红波段反射率构成的NIR-Red空间中,像素点通常会呈现三角形分布,随着植被覆盖度的增大,像元沿着虚线箭头向A点移动;随着土壤水分的减少,像元沿着实线箭头由B点向C点移动,如图2a所示。
裸土点分布在NIR-Red空间三角区域的下边界,即BC线为土壤线[1],可以表示为:
N=f(R;m,d)=mR+d
(1)
其中,d、m分别为土壤线的截距和斜率;R、N分别为像元在近红外波段和红波段的反射率值。
土壤水分是影响裸土反射率的最大因素,这种现象在NIR-Red特征空间的三角区域上表现为含水量不同的裸土点分布在三角区域下方的不同位置。因此,文献[20]提出了垂直干旱指数(perpendicular drought index,PDI),利用空间中任意一点E到与土壤线垂直的直线l的距离EF表示土壤干旱状况,可以简单有效地监测土壤水分,如图2b所示。本文采用文献[21]提出的MPDI,数学上可以表示为:
(2)
其中,Rv、Nv为全植被覆盖点的反射率,从时间序列影像中可得Rv、Nv分别为0.03、0.7[10];v为植被覆盖度,本文采用与文献[10]一致的计算方法。

图2 NIR-Red特征空间和PDI模型
2.2 目标函数的构造
2.2.1 数据项
本文根据土壤线(1)式中的线性关系,构造目标函数的数据项,即
(3)
其中,xi、yi分别为从卫星影像中直接获取的土壤点集合中第i个像元在近红外波段和红波段的反射率值;n为土壤点集合中的像元个数。
数据项的数据来源和2.2.2节正则项的数据来源不同,这里用xi、yi表示,而不采取统一的R、N表示。
2.2.2 正则性
基于MPDI可以得到土壤含水量S[9],MPDI与土壤含水量的关系如下:
S=aMPDI+b
(4)
其中,a、b为线性拟合系数。本文期望由土壤线估计土壤水分尽量逼近实测的土壤水分,因此构造了目标函数的正则项,即
(5)
其中,Fj、Sj分别为已知的实测站点土壤含水量和估计土壤含水量;t为实测站点个数。将(2)式、(4)式代入到(5)式中,得到最终的正则项为:
(6)
2.2.3 总体目标函数
根据(3)式和(6)式,可以得到总体目标函数为:
(7)
其中,λ为用来平衡数据项和正则项的权重。
目标函数(7)式第1项是数据项,根据土壤线的公式构造,拟合数据项的数据来源于遥感影像的土壤点(近似裸土点)像元;目标函数(7)式第2项是正则项,根据估计水含量与实测水含量误差构造,拟合水含量模型参数的数据来源于地面站点对应的遥感像元。
卫星影像数据很难保证提供纯裸土像元,因此第1项估计土壤线是不准确的,这会导致第2项水含量估计误差变大。为了达到整体目标函数最小,第2项的加入会调整第1项的土壤线参数,使其向着较正确的方向发展。此时,第1项估计土壤线逐渐的准确会使第2项估计水含量越来越准确。
在这种交叉迭代估计中,土壤线和水含量的估计精度都会得到较好地提高。
2.3 目标函数的求解
本文引入与土壤线垂直的直线l:y=kx(其中k=-1/m)。由于m+1/k=0,将目标函数(7)式的数据项分解为:
(8)
基于MPDI模型中像素点到直线l的距离表征水含量,将目标函数(7)式的正则项分解为:
(9)
目标函数的求解则转换为对2个子函数(8)式、(9)式的求解。
(1) 子函数1求解m、d,固定k(即将k看成常数)。(8)式的解为:
(10)
d=
(11)
(2) 子函数2求解a、b、k。同理,子函数2也是1个方程求2组未知数的问题。将子函数2分为2个子问题求解:① 子问题1求解a、b,固定k;② 子问题2求解k,固定a、b。
子问题1的(9)式解为:
(12)
(13)
关于m的公式非常复杂,这也是不直接求解m而引入k来求解的原因。按上述方法,最终可以整理成一个关于k的一元四次方程。在数学上,4次以及4次以下的一元多次方程都是有求根公式的,本文根据费拉里法求根公式解得最终的k。
2.4 算法框架
MPDI模型中,估计土壤含水量是通过土壤线参数计算得到的,实际土壤含水量已知。因此,本文采用估计土壤含水量与实测土壤含水量的误差作为目标函数的正则项,修正数据项中土壤点并非都是纯裸土点的不足,以提高土壤线求取的准确度。
算法步骤如下所述。
(1) 输入Landsat8卫星影像。
(2) 计算Red波段反射率和NIR波段反射率。
(3) 获得初始土壤点集合(R,NIRmin)。
(4) 拟合初始土壤点的回归方程,获得参数m的初始值。
(5) 按地理坐标寻找与站点匹配的像元点。
(6) 迭代过程外循环i从1到n。
(7) 内循环j从1到t。
(8) 初始化参数k(其中k=-1/m)。
(9) 利用(12)式和(13)式求解a、b。
(10) 利用(9)式求解k。
(11) 内循环结束。
(12) 利用(10)式、(11)式求解m、d。
(13) 更新参数。
(14) 外循环结束。
(15) 得到土壤线后计算MPDI,建立MPDI与水含量的关系。
3 结果与分析
3.1 土壤线实验结果
水体常分布在裸土点的下方。在无水体或水体较少的区域,获得的土壤点(R,NIRmin)可以被认为是裸土点,而在有河流的区域,此方法提取的裸土像元会包含水体,直接拟合土壤点获得的土壤线将会受到水体的影响而产生偏差。
9幅时间序列上拟合的土壤线结果如图3所示。

图3 9幅时间序列上拟合的土壤线结果
其中,①为直接拟合土壤点获得的土壤线,可以看出9幅影像中,这种方法都受到了水体的干扰,尤其是第2幅(2013-07-06);②为本文算法拟合出的土壤线,可以看出本文加上了实测数据的约束,明显抵抗了水体以及噪声带来的影响;为了不影响最终土壤线的对比观测,将收敛过程以直线l(过原点且垂直土壤线的直线)显示,③为最终收敛的结果。
9幅卫星影像获得的土壤线斜率m以及将其用于MPDI计算后得到的MPDI结果与实测数据的相关系数见表2所列。

表2 Yanco区域时间序列结果
3.2 MPDI与土壤含水量
(1) MPDI与实测土壤水分的负相关性。Amani提出了利用5条不同土壤类型土壤线的平均值[7]并在后续研究[10]中使用了统一的土壤线来研究MPDI与实测土壤水分的关系。文献[10]Amani算法与本文算法的MPDI计算结果与实测数据的相关性对比如图4所示。从图4可以看出,本文算法得到的负相关性明显高于文献[10]Amani算法的负相关性。
(2) 估算含水量与实测含水量对比。本文在226个站点数据中选择75%(约170个)的数据用于训练估计含水量S与MPDI的线性模型,即求取(4)式中的线性拟合系数a、b;剩下的25%(约56个)数据用于测试估算含水量与实测含水量的一致性。
在Landsat8时间序列影像上,对本文算法获得的土壤线和文献[9]中Amani算法提出的平均土壤线在估算的土壤含水量结果上分别计算了均方根误差RMSE、相对均方根误差百分比RRMSE以及相关系数,其中RMSE、RRMSE越小以及相关系数的绝对值越大,说明估算的结果越接近实测数据。

图4 MPDI与实测土壤水分的关系
估算的土壤含水量与实测土壤含水量结果如图5所示。从图5可以看出,本文算法提取的土壤线在土壤水分监测中比文献[9]的Amani算法在精度上提高了很多。

图5 估算的土壤含水量与实测土壤含水量结果
4 结 论
土壤含水量和植被指数等反演都需要土壤线的参数。本文基于实测土壤水分与由土壤线估计的土壤水分之间的误差构造目标函数正则项,修正数据项中土壤点并非都是纯裸土点的不足,并在求解过程中,通过交叉迭代估计土壤含水量和土壤线,使得土壤含水量和土壤线的估计精度都得到较好的提高。此外,本文算法还有效地抑制了遥感图像中“噪声”像素,包括水体、铺面物体以及其他非植物物体等对土壤线探测的阻碍。本文提出的框架还可以进一步推广到土壤线与植被指数的求解,对干旱模型和植被指数模型的推广都有一定的应用价值。
在算法性能的分析过程中,土壤水含量不仅受土壤线的影响,同时还受到很多其他因素的影像,如地表温度等。本文在设计正则项时,只考虑了土壤线对估计水含量造成的误差,在后续的算法改进中,会考虑其他因素的加入,完善算法的性能。
