基于标签扩散的时序平滑社团检测算法

何 伟, 胡学钢, 杨恒宇

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230601; 2.安徽省科学技术情报研究所,安徽 合肥 230011)

0 引 言

复杂网络是多主体交互或关联系统的有效建模方法。现实世界中存在着大量的复杂网络,如Internet、社交网络、科学家合作网络、蛋白质相互作用网络等。

社团结构描述了复杂网络的一种非均质连接特性,即网络由不同的节点簇构成,簇内节点连接相对紧密,而簇间连接相对稀疏[1]。社团结构是网络中个体行为与整体功能之间的桥梁,对网络的结构和功能分析具有重要意义,针对社团结构物理意义和数学特性的研究因而成为近年来的研究热点[2]。

社团检测旨在揭示网络中所蕴含的社团结构,有助于网络结构的分析、网络功能的推断、网络拓扑的优化,是理解和探索网络结构与功能的关键问题。

传统的社团检测算法大多针对具有固定拓扑结构的静态网络,然而实际网络往往会随着时间推移发生改变。例如,在科学家合作网络中,新的研究者不断加入,已有研究者也会退出;不同领域的研究者会开展新的合作,原有合作也可能停止。这种变化导致网络中社团结构的持续演化。已有静态方法通常关注提高准确性或时间性能,而动态网络中的社团检测方法还需要考虑演化社团的时序平滑性,即连续时间片中检测出的社团结构不应有过大差异。针对动态网络中的社团检测问题,本文提出基于角色的演化标签扩散算法(role-based evolutionary label propagation algorithm, RELPA),结合已检测出的社团结构信息,能够提高连续时间片中社团结构的时序平滑性,同时引入演化过程中的结构差异信息,能够快速准确地检测出动态网络中的演化社团结构。

1 相关工作

文献[3]提出了一种基于密度的动态社团检测算法,该方法首先通过静态方法检测社团结构,然后检测下一时间片网络中节点和边的更新,用基于密度的方式将相关的更新节点重新分配隶属社团。

文献[4]提出了一种基于两步策略的动态社团检测算法,对于任意t时刻的网络快照进行静态社团检测,然后根据t-1时刻的社团检测结果,将原问题转化为最小化代价函数的优化问题,最后采用极值优化方法对t时刻的结果进行调整。

文献[5]提出了一种动态社团检测框架,该框架首先通过基于模块度的算法检测并记录t-1时刻网络快照中的社团结构,之后将t时刻发生变动的节点从社团结构中释放,即不属于任何社团,然后对这些自由节点重新赋予社团标签,使得整体模块度最大。在此基础上,文献[6]提出了一种改进算法,算法中的自由节点不仅包括在t时刻发生变动的节点,还包括这些节点周边的节点。

文献[7]提出了一种基于最大团的动态社团检测算法。对应的静态算法寻找网络中所有的最大团,将其中所有连通的k-1团视作社团。动态比较连续时间片中的网络,针对新网络中的变化节点重新搜寻最大团,然后更新k-1团,最终合并为新的社团。

文献[8]在标签传播算法(label propagation algorithm,LPA)[9]的基础上提出了一种动态社团检测算法。不同于标签传播算法中每个节点对应一个标签,该方法中每个节点保存一组可能的社团标签及其对应的概率,同时通过膨胀和剪枝来控制标签数目,以优化算法的时间性能。

文献[10]提出了另一种基于标签传播的动态社团检测算法,将t时刻网络中的置信度与t-1时刻网络中的置信度相结合进行标签传播,通过这种方式引入了相邻时间节点的网络信息,也包括其中隐含的社团结构信息。

文献[11]提出了一种动态博弈论社团检测算法。该算法将网络中的每个节点分别看作一位理性博弈者,每个博弈者与其邻居进行有关社团隶属的博弈,通过加入或离开某个社团来获得最大效益。当网络中出现纳什均衡时,所有节点的隶属即构成网络的社团结构。实验表明该方法能够准确判定社团数目,并能够得到较高的归一化互信息和模块度值。

文献[12]提出了一种基于非负矩阵分解的演化社团检测算法，证明了该算法与最大化演化模块度密度、演化谱聚类之间的等价性,并对其进行扩展,提出了半监督版本的演化非负矩阵分解。不同于传统的半监督方法,该算法将先验信息与目标函数相结合,有助于在求解过程中跳出局部最优同时不增加时间复杂度。在人工数据集和真实数据集上的实验表明了该算法具有优异的准确性。

2 时序平滑社团检测方法RELPA

本文在基于角色的标签扩散算法(role-based label propagation algorithm, RLPA)基础上,提出演化社团检测方法RELPA。结合已检测出的社团结构信息确保连续时间片中社团结构的时序平滑性,通过定义时序置信度引入演化过程中的时序拓扑差异性信息,增强对社团微观结构变化的捕获能力。

2.1 基于角色的标签扩散算法

标签扩散算法的具体描述如下:

一个网络可以用图G(V,E)来表示,其中,V为网络中节点的集合;E为网络中边的集合。对于节点i(i∈V),用Li表示节点标签,N(i)为i的邻居节点集合。

初始时,为每个节点赋予不同的标签,Li=i。接下来,对每个节点的标签进行迭代更新。每次迭代中,节点的标签更新为邻居节点中偏好权值最高的标签,即

(1)

其中，Nl(i)为节点i邻居节点中标签为l的节点集合;si(l)为节点i上标签l的衰减值;wij为节点i对节点j的偏好权值。原始的标签扩展算法中,偏好权值为1,节点更新为邻居节点中数量最多的标签。

如果有多个标签满足此条件,那么将这些标签作为候选,从中随机抽取一个作为节点的更新标签。如果节点当前的标签在候选集中,那么节点保持当前标签。每次迭代中,节点的更新顺序完全随机。在整个标签扩散的过程中,连接紧密的节点标签通常会快速趋于一致。

标签扩散带来的随机性使得算法具有较差的鲁棒性和稳定性。当网络社团结构较弱时,扩散机制可能导致网络中的大部分节点隶属于同一社团,从而得到无意义结果。为此,文献[13]提出一种基于角色分析的标签扩散算法RLPA,引入与社团角色相关的度量作为节点偏好,利用局部指标调整节点更新策略,以提高算法准确性。RLPA算法将传播过程分成平衡传播和膨胀传播2个阶段。

平衡传播阶段的目的是稳定社团核心节点标签,让桥节点标签振荡,该阶段的节点对偏好权值为:

wij=1+Dn(cj)-Ln(j)

(2)

其中,Dn(cj)为社团cj的归一化边密度;Ln(j)为节点j的归一化隶属度。

归一化边密度定义为:

(3)

其中,C为当前所有社团的集合；D(c)为社团c的社团密度,即社团内边数与最多可能边数的比值:

(4)

其中,E(c)为社团c中的边集合;V(c)为社团c中的节点集合;|X|为集合X的势。

归一化隶属度定义为:

(5)

其中,V为网络中所有节点的集合;L(i)为节点i的隶属度,即节点社团内度数与节点度数的比值:

(6)

其中,d′(i)为节点i的社团内度数,即节点i在社团内的邻居节点个数。

平衡传播阶段桥节点标签反复振荡,无法收敛。算法检查每次迭代中标签变化的节点数,将变化节点数上升记作1次振荡,并根据网络规模设定最大振荡次数为lgn,其中n为网络中的节点个数。

膨胀传播阶段,核心节点标签迅速扩散,加速算法收敛,这一阶段的节点对偏好权值为:

wij=1+Ln(j)C(j)

(7)

其中,C(i)为节点i的度数中心度,定义为节点的社团内度数与社团中内部度数最高节点度数的比值:

(8)

另外,RLPA算法通过节点的局部影响力度量Burt约束系数(Burt’s constraint score)作为节点更新顺序依据[14],其定义为:

(9)

其中,Vi为节点i自我中心网络中的节点集合,包含节点i及其邻居节点;pij为节点j与节点i之间的相对关联强度，即

(10)

其中,aij为邻接矩阵A中的元素。

2.2 结合时序平滑信息

在动态网络中,由于社团演化具有连续性,相邻网络快照中检测出的社团结构不应差异过大。本方法在标签扩散的节点偏好权重中引入奖惩系数,以利用前序社团结构信息。定义t时刻的节点j对节点i的标签权重为：

(11)

由(11)式可以看出,t-1时刻先验社团结构信息中社团间节点对与社团内节点对的奖惩系数之比为α/(2-α)。当α=1时,两者奖惩系数之比为1,此时节点偏好权值仅考虑t时刻网络结构信息,不考虑前一时刻社团结构的影响,算法等价于RLPA算法。随着参数α减小,两者奖惩系数之比逐渐变小,前一时刻社团结构对标签权重的影响变大,在计算节点间标签权重时奖励前一时刻的社团内节点对、惩罚前一时刻的社团间节点对。当α=0时,前一时刻社团结构信息的影响达到最大,两类节点对的奖惩系数比例降为0,此时,节点间标签权重仅考虑前一时刻属于同一社团的节点对偏好权值。

2.3 结合时序拓扑差异信息

通过奖惩系数,算法将前一时刻网络快照中的社团结构信息引入当前时刻的社团检测过程,但并未考虑不同类型节点在时序变化中的差异。在网络演化过程中,网络结构的局部变化并不是均质的,一些节点的变化较大,另一些则变动较小,奖惩系数无法反映网络局部结构的变化差异。为了解决这一问题,本文定义节点的时序结构相似度和节点对的时序置信度。

节点的结构相似度可以通过多种方式度量,本文选择的Jaccard相似度函数如下:

(12)

由(12)式可知,在2个连续的网络快照中,节点i的邻居节点变化越小,其在相邻时刻邻居节点变化越小,其时序结构相似度越大。当节点i在t-1时刻和t时刻的邻居节点没有发生变化时,其时序结构相似度为1,即局部网络结构相同。

(13)

由(13)式可以看出,当i节点和j节点的时序结构相似度均较大时,节点对(i,j)就具有较高的时序置信度,反之则具有较低的时序置信度。将时序置信度引入(11)式,得到新的标签权重计算公式,即

(14)

将RLPA的两阶段偏好权值公式分别代入(14)式,即得到RELPA在平衡传播阶段和膨胀传播阶段的标签权重计算公式。

2.4 RELPA伪代码

结合本节前文的算法介绍,RELPA的伪代码如算法1所示。

算法1RELPA伪代码

输入: 演化网络G1(V1,E1),…,GT(VT,ET), 衰减系数δ, 奖惩系数α

输出: 社团结构C1,…,CT

fort∈{1,…,T}do

fori∈Vtdo//初始化(节点标签等)

L(i)←1

s(i)←1//节点的标签衰减系数

Ni←{j|(i,j)∈Et}

V′←argsort(B(i))//确定节点更新顺序

ift=1 then//计算连接偏好权值

for {(i,j)|eij∈Et} do

Wij=1

else

fori∈Vtdo

forj∈Nido

ifi∉Gt-1orj∉Gt-1then

Wij=1

else

while not 满足迭代终止条件 do//标签传播

fori∈V′ do//平衡传播和膨胀传播

if not 满足平衡传播终止条件 then

else

updateD(ci′)

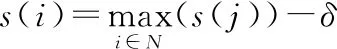
fori∈Vtdo//更新归一化隶属度和中心度

updateLn(i)

updateC(i)

forct∈Ctdo//更新密度和归一化密度

updateD(ct)

updateDn(ct)

returnC1,…,CT

2.5 时间复杂度分析

在RLPA的基础上,本文算法花费额外的时间计算时序置信度和标签对累加权值。

根据(7)式,当旧网络中的节点集包含于新网络时,需要对所有存在连边的节点对计算时序结构相似度,此时该计算时间复杂度最高,为O(d′m),其中d′为网络中的最大节点度数。计算时序置信度时需要计算2个节点的时序相似度及其乘积,时间复杂度均为O(d′m)。

标签更新迭代时间复杂度为O(km+nd2),其中，k为算法的迭代次数;n为网络中的节点个数；d为网络中节点的平均度数。

综上所述,RELPA的时间复杂度为O(d′m+km+nd2)。由于实际网络的稀疏性,节点的平均度数通常远小于节点数目n,可以视作常数。因此,本文算法在实际网络上的时间复杂度为O(d′m)。

3 实验分析

3.1 实验数据集

本实验采用企业邮件网络Enron(http://www.cs.cmu.edu/～enron/)和论文合作网络DBLP(http://projects.csail.mit.edu/dnd/DBLP/)2个数据集,数据集的基本统计信息见表1所列。

表1 实验数据集统计

Enron数据集记录了安然公司的电子邮件通信,本实验选取2001年的12个月的数据。原始网络数据为有环有向多边无权图,每个节点代表一位安然员工,每条边代表一封邮件,方向为邮件发送方到接收方。本实验按月划分网络快照,节点集合包含网络中最大弱连通分支中的节点。忽略边的方向,合并节点对之间的边并删除所有的环,每条边权值为1。

DBLP数据集记录了计算机领域论文合作情况,本实验考察其中2001—2010年的数据。原始网络数据为无环无向多边无权图,每个节点代表一位科学家,每条边代表一次论文合作。本实验按年划分数据集,节点集合为整个网络中最大连通分支中的节点,合并节点对之间的边,每条边的权值为1。

3.2 参数设置

根据文献[15],RELPA的跃进衰减系数δ设为0.10，奖惩系数α设为0.5;评价指标中动态模块度系数设为0.5。

3.3 实验结果

实验对比RELPA、LPA、RLPA、FacetNet、DLPAE 4种算法，在2个真实网络数据集上的表现[4,9,10,13],分别考察社团检测结果对应的动态模块度[16]和社团个数,结果如图1、图2所示。

图1 Earon邮件网络算法对比结果

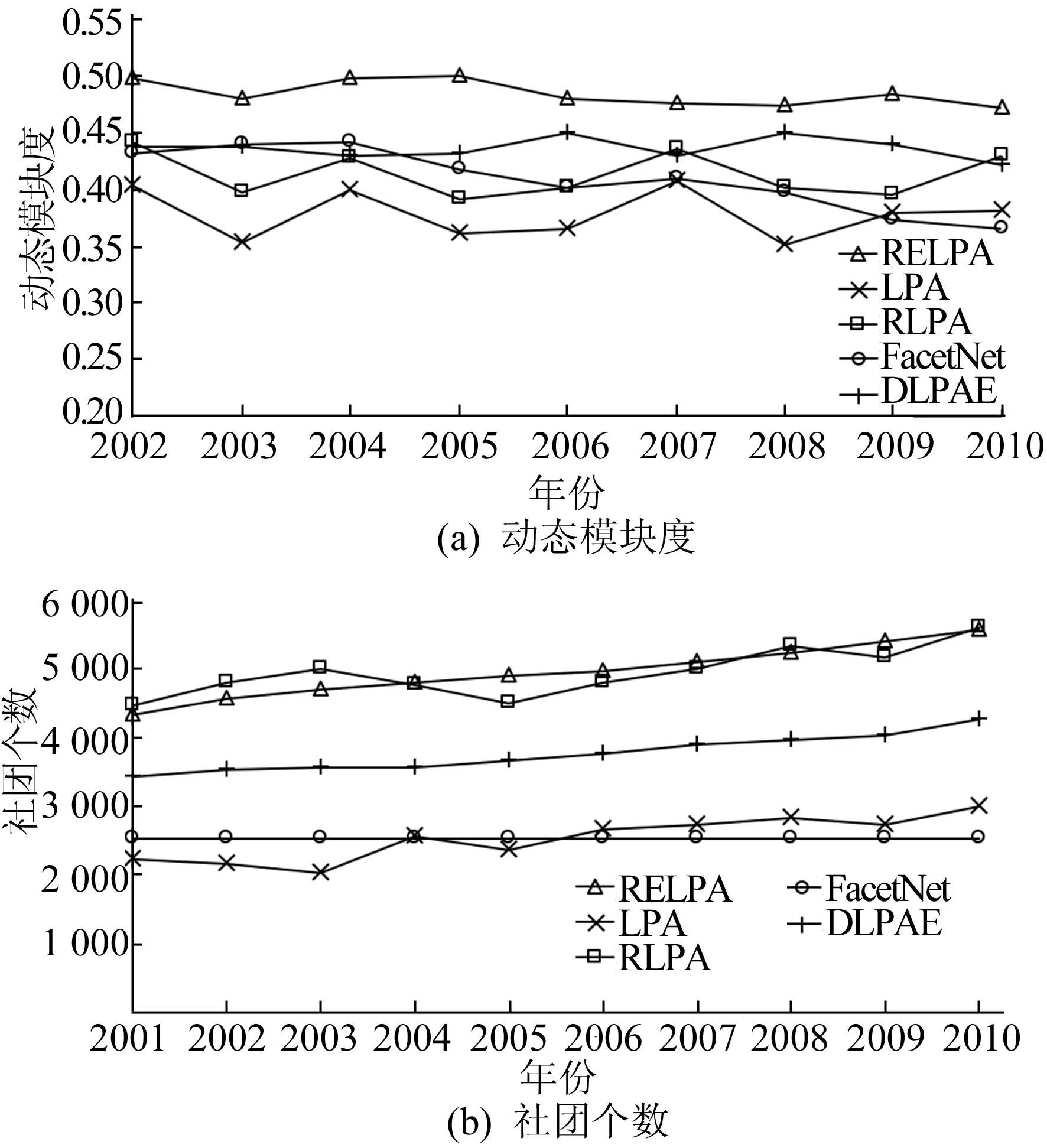
图2 DBLP论文合作网络算法对比结果

从图1a、图2a可以看出, 3种演化社团检测算法在2个数据集上的表现均优于静态社团检测算法 LPA,本文算法 RELPA表现最好。RLPA算法在LPA算法的基础上引入与社团角色相关的节点偏好和更新策略,与LPA算法相比准确性较高,但在动态社团检测上,未考虑上一时间片的网络结构信息,准确度与FacetNet接近,低于DLPAE和RELPA。与FacetNet相比,2类基于标签扩散的动态社团检测算法得到的动态模块度值更加稳定。

从图1b、图2b可以看出，5种算法检测到的社团个数变化。FacetNet针对多个社团个数取值进行检测,根据结果对应的软模块度值选择最优社团个数,并在之后的社团检测中保持社团个数恒定。与RLPA、LPA相比,由于引入了时序平滑,动态社团检测算法RELPA、DLPAE得到的社团个数趋势均更为平稳。其中, Enron 邮件数据集伴随了公司部门及人事变动,社团个数略有起伏与这种变化相符;DBLP 计算机论文合作数据集伴随了学科的逐步发展和科研团体的新增,社团个数呈现平稳递增的趋势与这种变化相符。

4 结 论

随着大规模动态网络数据的涌现,演化社团检测方法研究将具有越来越广泛的应用前景。与静态社团检测方法相比,演化社团检测对社团的时序平滑性提出了要求,在时间性能上也有较高的要求。本文提出了一种基于标签传播的演化社团检测方法,并将当前网络快照与不同时间片的社团信息相结合,同时引入了不同网络快照中社团的结构差异信息。对比实验表明本文提出的方法能够准确地挖掘出动态网络中的演化社团。