Schur不等式的一个注记

廖 平

（四川职业技术学院教师教育系，四川遂宁629000）

矩阵特征值估计是矩阵分析领域重要的热点问题之一。1909 年，Schur 给出了估计（即Schur 不等式[1-2]），其中λi表示矩阵A 的特征值，‖ A ‖F表示矩阵A 的Frobenius 范数，当A 为正规阵时等号成立。对于非正规阵，文献[3]将其改进为

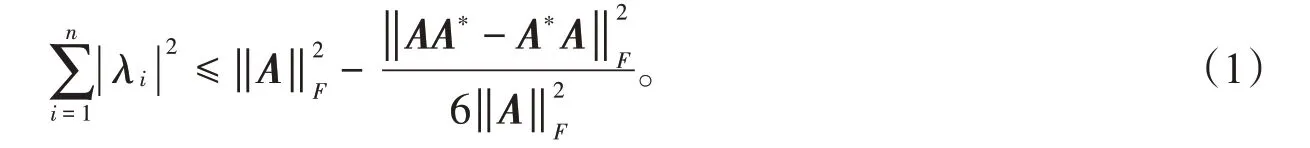
文献[4]对其做了进一步优化。Kress等在文献[5]中得到如下结果：

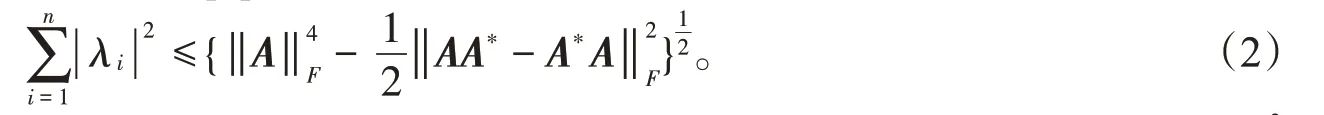
上述结果可直接用于矩阵特征值分布估计以及奇异性分析[6-8]。不难看出，以上改进均与有关，该项也常作为矩阵非正规性度量。但由于计算量较大，这会影响到（1）（2）式的实际运用，尤其当矩阵阶数较高时。为方便应用，Kress在文献[5]中给出了如下估计：

然而对于高阶矩阵，行列式的计算量是巨大的。鉴于此，本文尝试给出的一些易于计算的下界，以方便高阶矩阵特征值的估计。下文中Cn×n表示所有n阶复方阵组成的集合，且假设n ≥2，不考虑n=1时的退化情形。

先给出如下熟知的引理。

引理1设A ∈Cn×n为n 阶Hermitian 矩阵，λ 为其最大模特征值，则对任意单位向量x，有

证明设λ1、λn分别为矩阵A的最大、最小特征值，由Hermitian矩阵的性质知，对任意单位向量x有λ1≥x*A x ≥λn，即| x*A x |≤max{| λ1|, | λn|}= |λ|。

定理1 设A ∈Cn×n，则对任意单位向量x，有

证明显然矩阵B=AA*-A*A 为Hermitian 矩阵，设矩阵B 的特征值按模从大到小依次为，则由引理1可知

在定理1 中若取向量x 为一些特殊向量，即可得到一些容易计算的界。如取向量x=ei=(0,0,…,1,…,0)T，则由定理1及式（2）可得推论1。

推论1 设A ∈Cn×n，则，其中

证明取x=(0,0,…,1,…,0)T带入定理1得，由式（2）即得所要结果。

推论2设A ∈Cn×n，则，其中

定理1的结论是比较容易得到的。若再结合矩阵的自身特点，还可进一步将其优化为如下结果。

定理2设A ∈Cn×n，则对任意单位向量x，有

证明设矩阵B=AA*-A*A特征值按模从大到小依次为 |μ1|≥| μ2|≥| μ3|≥…≥| μn|，由于trB=0，从而其特征值μ1,μ2,μ3,…,μn满足，故对最大模特征值μ1，必有若干个（不防设为k个，k ≤n-1）相反符号的特征值（这里记为μ11,μ12,μ13,…,μ1k），其和与μ1相抵或。从而有

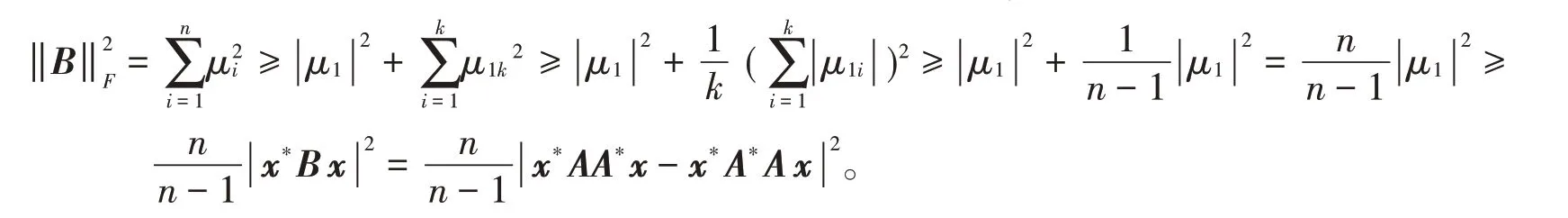
不难看出定理2改进了定理1。同时，推论1、推论2亦可相应地改进为推论3、推论4。

推论3设A ∈Cn×n，则，其中

推论4设A ∈Cn×n，则，其中

另外，容易计算AA*-A*A 的第i 个对角元dii=αi-βi，其中，与推论1和推论3相同，且，故还可有如下估计。

推论5设A ∈Cn×n，则，其中

最后将实际估计时常用的式（3）与推论5做一个简单的分析比较。在式（2）中，AA*-A*A的第i个对角元dii=αi-βi，其中αi，βi与推论5相同。当2时，推论5将优于式（3），其余情况则式（3）比推论5更好。