中考“三数”大扫描

文 刘 燕

平均数、中位数和众数从不同的角度反映一组数据的集中趋势，都可作为数据一般水平的代表。其中平均数反映了一组数据的平均大小，常用来代表数据的总体“平均水平”。中位数像一条分界线，将数据分为两个部分，用来代表一组数据的“中等水平”。众数是指出现次数最多的数据，用来代表一组数据的“多数水平”。只有理解这三个统计量的概念，运用相关知识进行数据分析，才可以得出全面的评价，有助于在解决实际问题时做出正确的决策。

考点一、算术平均数与加权平均数

例1 （1）（2020·浙江湖州）数据-1，0，3，4，4的平均数是（ ）。

A.4 B.3 C.2.5 D.2

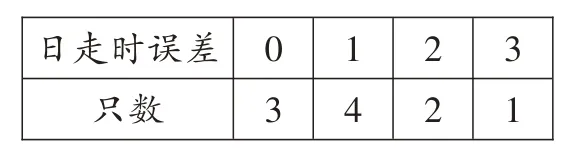
（2）（2020·江苏苏州）某手表厂抽查了10 只手表的日走时误差，数据如下表所示（单位：s）：

?

则这10 只手表的平均日走时误差（单位：s）是（ ）。

A.0 B.0.6 C.0.8 D.1.1

【分析】（1）根据题目中的数据，可以求得这组数据的平均数，本题得以解决。

（2）与（1）不同，表格告诉我们，日走时误差为 0 的有 3 只表，日走时误差为 1 的有 4 只表，日走时误差为2 的有2 只表，日走时误差为3的有1只表，利用加权平均数的计算方法进行计算。

解 ：故选D。

【点评】（1）考查算术平均数，（2）考查加权平均数，解答关键是正确区分算术平均数和加权平均数。（2）中的数据的平均数不仅与各个数据的值有关，而且与各个数据的“重要程度”，也就是“权”有关。

考点二、众数与中位数

例2 （2020·湖南岳阳）今年端午小长假复课第一天，学校根据疫情防控要求，对所有进入校园的师生进行体温检测，其中7 名学生的体温（单位：℃）如下：36.5，36.3，36.8，36.3，36.5，36.7，36.5。这组数据的众数和中位数分别是（ ）。

A.36.3，36.5 B.36.5，36.5

C.36.5，36.3 D.36.3，36.7

【分析】将这组数据重新排列，再根据众数和中位数的概念求解即可。

解：将这组数据重新排列为36.3，36.3，36.5，36.5，36.5，36.7，36.8，所以这组数据的众数为36.5，中位数为36.5。故选B。

【点评】本题主要考查众数和中位数的概念。求一组数据的众数的方法：找出频数最多的那个数据，若几个数据频数都是最多且相同，此时众数就是这多个数据。将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数。

考点三、三数的综合运用

例3 （2020·天津）农科院为了解某种小麦的长势，从中随机抽取了部分麦苗，对苗高（单位：cm）进行了测量。根据统计的结果，绘制出如图的统计图1和图2。

请根据相关信息，解答下列问题：

（1）本次抽取的麦苗的株数为_______，图1中m的值为_______；

（2）求统计的这组苗高数据的平均数、众数和中位数。

【分析】（1）可利用条形统计图中13cm 长的株数和扇形统计图中它所占的百分比，求得本次抽取的麦苗的株数，也可由条形统计图各组数据相加求出麦苗的株数。m的值则可根据扇形统计图中的数据计算求得。

（2）根据条形统计图中的数据，计算出平均数，再根据众数和中位数的概念求出答案。

解：（1）本次抽取的麦苗有2÷8%=25（株），

m%=1-8%-12%-16%-40%=24%，

所以m=24。

或：由条形统计图得本次抽取的麦苗株树为2+3+4+10+6=25（株）。

其中17cm 的麦苗株数为6 株，故其所占的比为6÷25=24%，则m=24。

故答案为：25，24。

（2）观察条形统计图，这组麦苗的平均数是：

这组数据中16出现了10次，出现次数最多，所以这组数据的众数为16。

将这组数据按从小到大的顺序排列，处于中间位置的数是16，所以这组数据的中位数为16。

答：这组苗高数据的平均数是15.6，众数是16，中位数是16。

【点评】本题考查条形统计图、扇形统计图、加权平均数、中位数和众数，解答本题的关键是读懂扇形统计图与条形统计图，并从不同的统计图中获取信息、收集数据，对数据进行整理、分析，得出答案。