课本题 变式题 中考题

文 姚雅萍

近几年的各地中考试题，选材贴近生活，背景越来越新，而且考题都立足教材例题、习题。下面我们从一道教材的习题出发，逐步走进2020年中考题。

【课本原题】（苏科版数学教材九年级上册第123 页习题第3 题）要从甲、乙两名运动员中选出一名参加校际100 米比赛，对这两名运动员进行了10次测试，成绩如下（单位：s）。

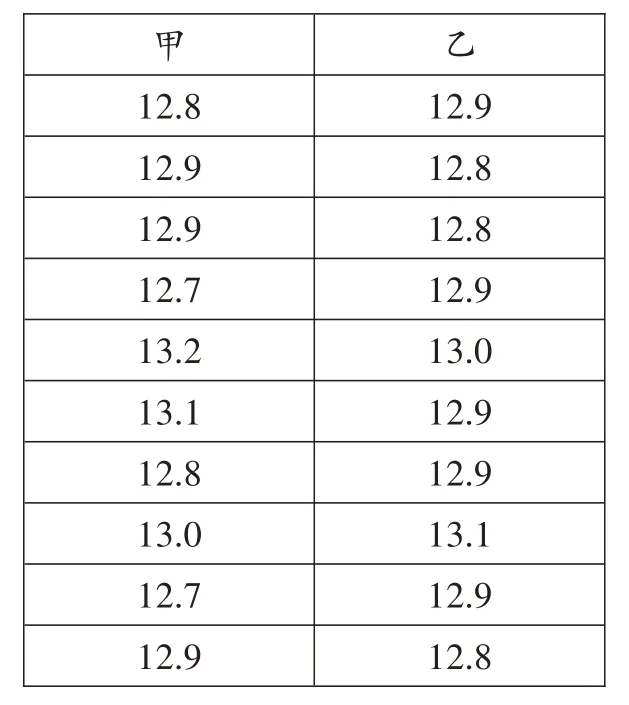
______________________12.9 12.8______________________12.8________________________12.9________________________13.0______________________12.9______________________12.9______________________13.1______________________12.9______________________12.8________________________甲 乙______12.8_____________________12.9 12.9_____________________12.7______________________13.2______________________13.1_____________________12.8_____________________13.0_____________________12.7_____________________12.9_____________________

根据测试成绩，你认为选派哪一名运动员参赛更好些？为什么？

【解题思路】

我推荐乙参加校际100 米比赛，理由如下：两人100 米比赛10 次测试的平均成绩相等，说明甲、乙两人实力相当；但乙的10 次测试成绩的方差比甲小，说明乙发挥较为稳定，所以我推荐乙参加比赛。

【点评】本题根据提供的成绩，计算甲、乙两名运动员的平均成绩和方差后作出选择。方差的大小能反映一组数据的波动大小，一般而言，一组数据的方差越小，这组数据就越稳定，因此本题可以用样本方差的大小来衡量甲、乙两名选手百米比赛成绩的稳定性，从而决定选谁参赛。当然也可以从其他方面考量，如：我推荐甲参加校际100 米比赛，理由是两人100 米比赛10 次测试的平均成绩相等，说明甲、乙两人实力相当；但甲10次测试中有两次成绩是12.7 秒，而乙的最好成绩是12.8秒，这说明甲更具有黑马潜质，如果状态好，发挥好，能冲击更好的名次（如破纪录），所以我推荐甲参加比赛。

【小结】本题考查平均数、方差的计算和理解。方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定。

【变式题】某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛。在最近的10次选拔赛中，这两个人的跳远成绩（单位：cm）如图所示：

根据图中信息，解答下列问题：

（1）分别求甲、乙两名运动员成绩的极差；

（2）求甲运动员成绩的中位数、众数；

（3）这两名运动员的成绩各有什么特点？

【分析】从折线统计图中直接获取甲、乙两名运动员成绩（单位：cm）。

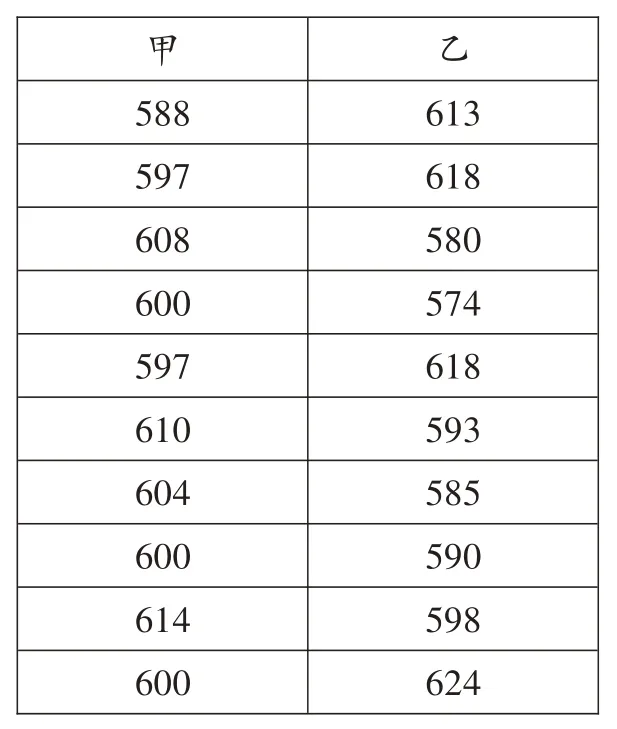
_________________________613 618_________________________580_________________________574_________________________618_________________________593 585_________________________590_________________________598_________________________624________________________甲 乙______588_____________________597 608_____________________600______________________597_____________________610_____________________604 600_____________________614_____________________600______________________

（1）求极差的方法是用一组数据中的最大值减去最小值；

（2）根据中位数、众数的概念即可求出；

（3）答案不唯一，符合题意即可。

解：（1）甲、乙两名运动员成绩的极差分别为26cm、50cm。

（2）将这组数据按从小到大排列，由于有 10 个数，第 5、6 位都是 600，则中位数为600；因为600 出现的次数最多，则该组数据的众数为600。

（3）答案不唯一，如：甲的成绩比较稳定，波动小；乙的成绩不稳定，波动较大。

【点评】此题从折线统计图中不但可以得到甲、乙两名运动员最近10次选拔赛的跳远成绩，而且可以看出训练对各人的影响效果。分析时我们要从平均数、中位数、众数、极差等多方面综合分析。

【中考题一】（2020·湖北黄冈）甲、乙、丙、丁四位同学五次数学测验成绩统计如下表所示，如果从这四位同学中，选出一位同学参加数学竞赛，那么应选（ ）去。

A.甲 B.乙 C.丙 D.丁

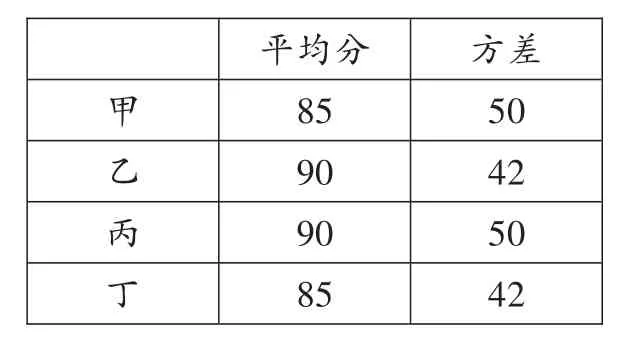
_____________________________方差___________________________50__________________________42__________________________50__________________________42甲________乙________丙________丁平均分____________85______________90______________90______________85______________

【解题思路】本题由表格提供信息，考查数据的集中程度和波动大小。从表格数据可以看出：乙、丙两名同学的平均成绩高于甲、丁两名同学的平均成绩，且乙同学的方差又小于丙同学的方差，说明乙同学的成绩好且稳定，因此选乙同学去参加数学竞赛。故选B。

【中考题二】（2020·湖北咸宁）如图是甲、乙两名射击运动员某节训练课的5 次射击成绩的折线统计图，下列判断正确的是（ ）。

A.乙的最好成绩比甲高

B.乙的成绩的平均数比甲小

C.乙的成绩的中位数比甲小

D.乙的成绩比甲稳定

【解题思路】本题从折线图中获取数据信息，考查平均数、中位数、方差。甲运动员的成绩为6、7、10、8、9，乙运动员的成绩为8、9、8、7、8。甲的最好成绩为10环，乙的最好成绩为9 环，A 选项错误；甲的成绩平均数为（6+7+10+8+9）÷5=8，乙的成绩的平均数为（8+9+8+7+8）÷5=8，成绩的平均数相等，故B选项错误；甲的成绩的中位数为8，乙的成绩的中位数为8，也是一样，故C 选项错误；甲的成绩的方差乙的成绩的方差所以乙的成绩比甲稳定，D选项正确。

【中考题三】（2020·浙江温州）A、B 两家酒店规模相当，去年下半年的月盈利折线统计图如图所示。

（1）要评价这两家酒店7—12 月的月盈利的平均水平，你选择什么统计量？求出这个统计量。

（2）已知A、B 两家酒店7—12 月的月盈利的方差分别为1.073（平方万元）、0.54（平方万元）。根据所给的方差和你在（1）中所求的统计量，结合折线统计图，你认为去年下半年哪家酒店经营状况较好？请简述理由。

A、B两酒店7—12月盈利折线统计图

【分析】首先从折线统计图中直接获取两家酒店7—12月的月盈利情况。（1）要评价两家酒店月盈利的平均水平，选取两家酒店月盈利的平均值，用求平均数的方法求解即可求得答案；（2）盈利的方差反映酒店的经营业绩，A 酒店的经营状况较好。

【解题思路】（1）选择两家酒店月盈利的平均数。

（2）我认为去年下半年A 酒店经营状况较好。理由：A 酒店盈利的方差为1.073，B 酒店盈利的方差为0.54，虽然从方差的大小来看，A 酒店盈利不稳定，但A 酒店盈利的平均数为2.5，B 酒店盈利的平均数为2.3。A酒店总盈利高于B酒店总盈利；而且从折线统计图中两家酒店的盈利走势来看，A 酒店的盈利越来越高，发展趋势良好。因此A酒店的经营状况较好。