CEM的波段选择方法研究及应用
2020-12-04陈艳拢王晓岚宋梅萍包海默
陈艳拢,王晓岚,李 恩,宋梅萍,包海默
1. 中国石油大学(华东)地球科学与技术学院,山东 青岛 266580 2. 国家海洋环境监测中心,辽宁 大连 116023 3. 大连海事大学信息科学技术学院,辽宁 大连 116026 4. 大连民族大学设计学院,辽宁 大连 116600
引 言
高光谱遥感可以利用成像光谱仪纳米级的光谱分辨率,获取大量窄且连续的光谱图像数据,同步得到地物的空间、辐射和光谱信息,在地物的细节描述和种类识别方面具有其他传感技术不可比拟的优势,被广泛应用于土地资源利用、灾害监测、地质评估、环境保护和农林调查等领域。 大量连续波段在刻画地物属性的同时,也产生出庞大的图像数据量,给数据分析和传输带来严重负担。 波段选择技术只保留包含更多有用细节信息的波段子集,不破坏原始数据的光谱特性和物理意义,在相关研究中备受关注。
波段的选择原则,通常是根据波段信息量和波段间关系进行定义,如方差、信息熵、信息散度、相关性等,主要以降低数据量且保持多样性为目的[1]; 也可以面向后续数据分析任务的特性进行定义,如高光谱解混任务中的最大单形体体积[2],异常探测任务中的高阶统计量等[3],以加快执行速度且利于任务效果为目的。 在面向任务的波段选择中,针对监督式情况下分类任务的研究较多[4],而对非监督情况下目标检测、定量分析等任务的研究却相对不足[5]。
另一方面,水是人类赖以生存、生活、生产的基础,然而,随着工农业经济的高速发展,大量的工农业废水、污水未经处理排入江、河、湖、海,特别是与人们日常用水密切相关的内陆河、近海河口等位置。 水的流动性加剧了水质的恶化,破坏了自然生态系统,威胁到了人类的正常用水,水质的污染问题已经成为制约我国经济可持续发展的关键因素,因此,对水污染的治理以及对水体的动态监测显得极为必要与紧迫。 传统的河流、湖泊水质监测主要是采用实地采样和实验室分析等方法,需要进行现场取点采样后送至实验室,通过化学分析技术进行分析,获得局部水域的水质情况。 这种监测方法虽然精确度高,但需耗费大量的人力、物力,且涵盖区域有限,不能对整体水域的水质情况进行实时监测与管理。
随着遥感技术的发展和成熟,遥感影像数据被广泛运用于水质监测中,弥补了水面采样的不足,能发现一些常规方法难以揭示的污染源的分布。 国内外许多学者陆续开展了通过遥感影像数据反演并估算水质参数含量的相关研究,如王丽艳[6]等利用MODIS数据反演呼伦湖水体总磷浓度并进行富营养化评价; 温新龙等[7]基于环境一号卫星数据对太湖的叶绿素a浓度进行反演; 冯驰等[8]利用GOCI影像和水体光学分类对叶绿素a浓度进行估算; 杜成功等[9]基于遥感数据反演太湖总磷浓度并研究其日内变化; 王云霞等[10]基于Landsat卫星影像研究总磷浓度反演; 马驰[11]基于遥感影像,采用回归分析的方法对松嫩平原水体的叶绿素a和悬浮物含量进行反演研究。 随着高光谱遥感技术的不断发展,其高分辨率、多波段、图谱合一的独特优点被广泛应用于水质监测,如潘洁等[12]通过提取高光谱遥感信息对射阳河口悬浮泥沙浓度定量反演; 徐良将等[13]利用实测光谱数据,通过微分法和波段比值法对总氮总磷浓度的反演等高光谱遥感在水质监测中的应用为水质的监测与管理提供了更多的数据支持,大大提高了水质参数的估算精度。
本研究针对待分析目标,面向数据分析任务研究有效的波段选择方法。 然后,将该方法用于水质中特定成分的定量分析。 使用六旋翼无人机搭载Nano微型机载高光谱成像仪(光谱范围为400~1 000 nm,共有270个波段),以辽河口为实验区进行高光谱数据采集,结合实地采样的数据,对辽河口的水质参数含量建立反演模型,进行系统的验证与估算。
1 显著性波段选择方法
高光谱数据波段数量多,信息量丰富,但特定地物的感兴趣因素通常集中表现在有限的光谱属性中,选择对待分析目标敏感的波段组合,可以更有效地建立反演和预测模型,常用基于皮尔逊相关系数进行波段选择。
1.1 皮尔逊相关系数波段选择方法
皮尔逊相关系数(Pearson correlation coefficient, PCC),又称皮尔逊积矩相关系数,是用于度量两个变量X和Y之间的相关程度,其值介于-1与1之间; 皮尔逊相关系数定义为两个变量之间的协方差和标准差的商,常用英文小写字母r代表,如式(1)
(1)
传统的波段选择方法是将各波段的光谱反射率信息与浓度作为两个变量,通过PCC度量二者之间的相关程度,选择若干具有代表性的波段进行建模。
1.2 信号匹配度的显著性波段选择方法
若将由待分析目标的定量变化值组成的向量看作目标信号,将所有光谱波段值组成的向量看作观测信号,采用信号匹配滤波器方法可以找出与目标向量匹配度高,且具有干扰抑制作用的波段集合。
约束能量最小化(constrained energy minimization, CEM)算法是有效的高光谱目标检测算法,基于该算法可以检测出与浓度向量匹配度高的波段集合。 但因为波段(尤其是相邻波段)间的相关性,所检波段集合存在冗余度高的问题。 为此拟结合正交原理,对候选波段集合中的观测向量进行正交投影,最大程度地选择与浓度向量匹配度高且与已有波段向量冗余度低的波段,具体算法原理和流程如下所述。
1.2.1 CEM算法原理
CEM算法是在已知目标而未知背景的情况下对目标进行检测的算法,其思想是先进行背景抑制然后进行匹配滤波,从而增强目标强度而抑制削弱背景或其他干扰信号,进而实现目标识别。 当目标信息占总成分的比例很小的时候,CEM算法检测效果更突出,适用于在未知的复杂背景下,对已知感兴趣目标的检测。
CEM算法流程图如图1所示,基本步骤如下:
(1) 对高光谱数据进行预处理,得到归一化后的二维数据r(L×Ν);
(2) 根据高光谱数据r,计算其自相关矩阵R;
(3) 确定目标向量d;
(5) 将归一化后的数据经过FIR滤波器,根据以下公式得到输出信号yi。
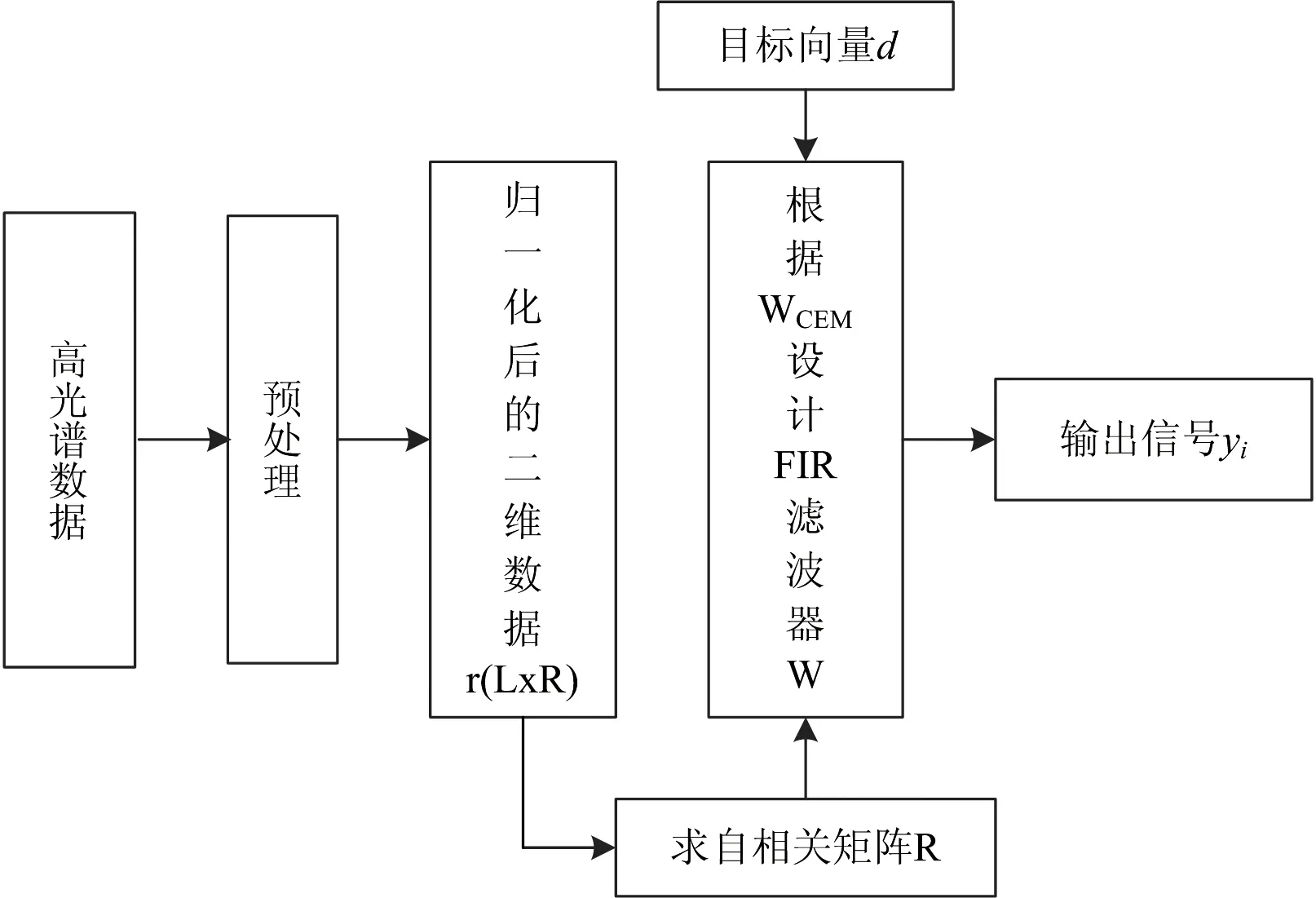
图1 CEM算法步骤Fig.1 Algorithmic steps of CEM
1.2.2 基于CEM的波段选择算法
本波段选择算法是利用CEM算法结合正交子空间投影(orthogonal subspace projection, OSP)进行波段选择。
正交子空间投影是将端元光谱矩阵M分为两部分: 感兴趣部分和非感兴趣部分,即Μ=[P,U],P代表感兴趣部分,U代表非感兴趣部分,在众多数据中,为了突出感兴趣部分而对非感兴趣部分进行抑制,OSP算法针对于非感兴趣部分U构造正交投影算子表达形式如(2)
U#=(UTU)-1UT
(2)
(3)
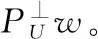
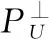
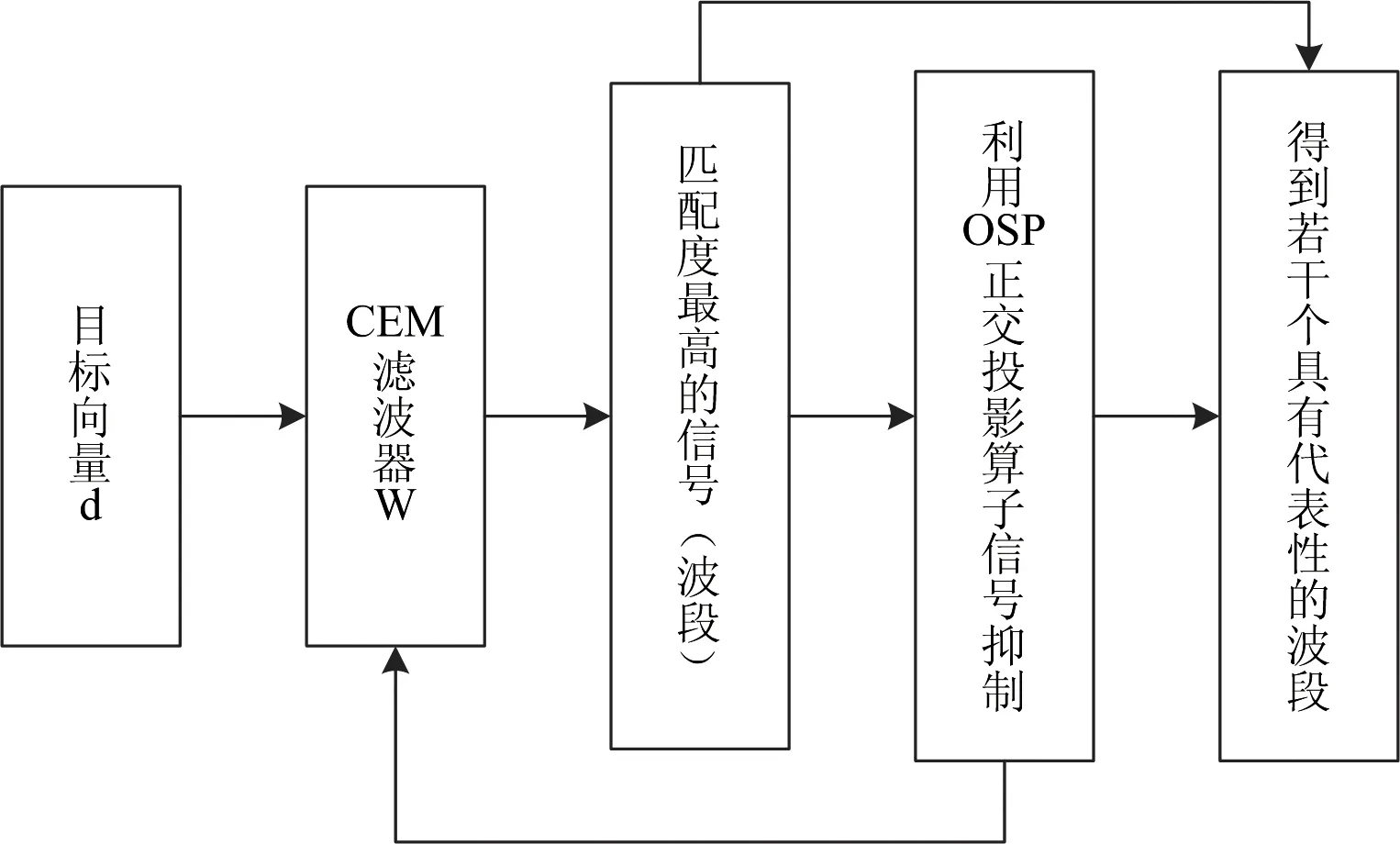
图2 CBS算法步骤Fig.2 Algorithmic steps of CBS
2 实验部分
2.1 研究区概况
辽河是中国七大河流之一,位于中国东北地区南部,界于东经117°00′—125°30′,北纬40°30′—45°10′之间,发源于河北省平泉县七老图山脉的光头山,流经河北、内蒙古、吉林、辽宁,全长1 345 km,注入渤海,被称为辽宁人民的“母亲河”。 但近年来由于大量非法排污,辽河成为我国污染最严重的河流之一,导致辽河水域生物无法存活,无法灌溉农业,威胁到了当地居民正常饮水。 故本研究区域选在辽宁省盘锦市盘山红海岸附近,位于辽河的入海口,此处有红海滩景观和世界最大的芦苇荡,是国家级自然保护区,水质的好坏也影响到了保护区的生态环境。
2.2 数据获取及处理
2.2.1 水样采集与分析
2018年10月11日在研究区内进行现场取样,规划了8个点位进行现场水样的采集,将取样用的采样瓶置入水中,采样过程中严禁水中杂质进入采样瓶,采集结束后做好密封操作,将采样瓶置于阴凉处,待八个点均取样结束后,尽快将水样送回实验室进行化学分析与水质参数含量测定。
2.2.2 高光谱遥感数据的采集
2018年10月11日(天气晴朗,采光条件良好),在现场水样提取的同时,进行高光谱数据的采集。 将Nano微型机载高光谱成像仪搭载在大疆公司的六旋翼无人机MATRICE600PRO上,飞行区域大小为1.5 km×0.5 km,飞行高度设置在飞行区上空400 m处,飞行速度控制在7.7 m·s-1。 采集结束后,利用Hyperspec Ⅲ高光谱数据分析软件对图像进行反射率校准和几何校准,然后在ENVI遥感图像处理平台上对图像进行拼接与裁剪操作,得到涵盖8个采样点的高光谱图像。
3 结果与讨论
3.1 总磷含量的反演
现场一共采取8个水样,选择5个样点用于总磷反演模型的构建,另外3个样点用来检验模型的反演精度。
3.1.1 基于PCC波段选择的总磷反演模型的构建
根据各个样点的经纬度信息在高光谱遥感图像上获取对应点的光谱反射率,再与总磷浓度进行皮尔逊相关性,如图3所示为总磷浓度与光谱反射率在不同波段处的相关程度。
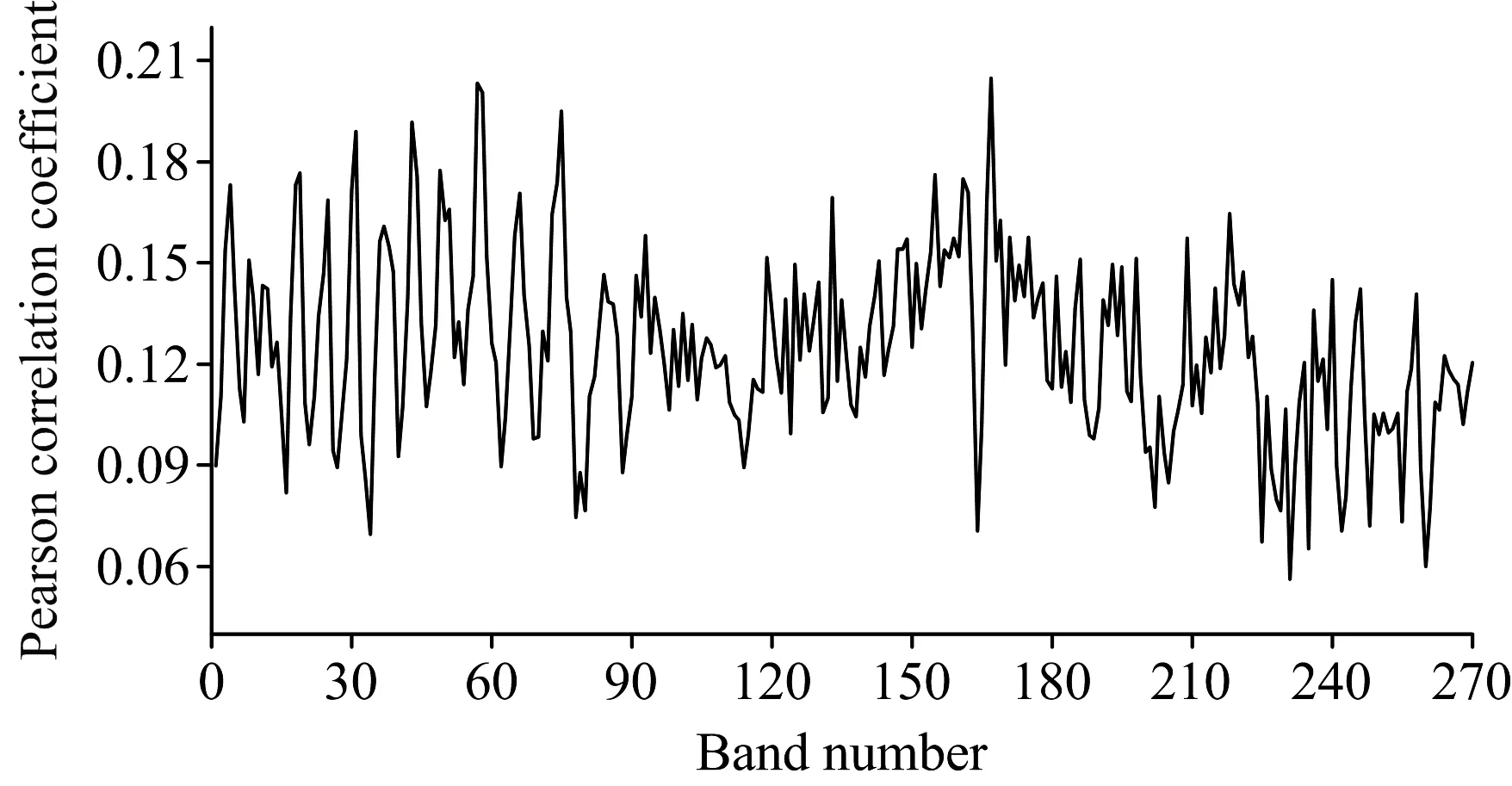
图3 总磷浓度与反射率在不同波段的相关程度Fig.3 Relevance between concentrationof TPand reflectivity in different bands
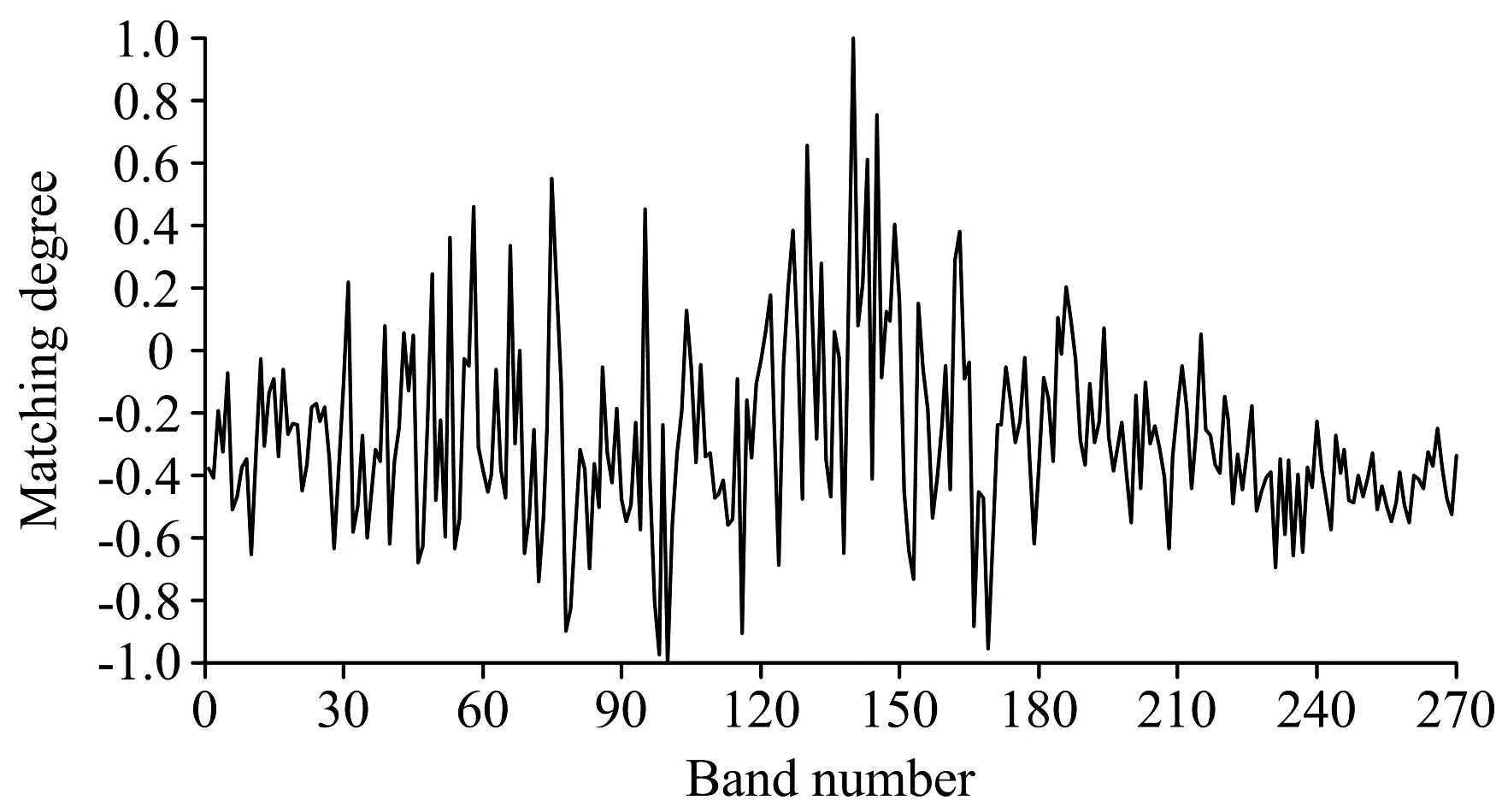
图4 各波段与总磷浓度矩阵的匹配程度Fig.4 Matching degree of each band withTP concentration matrix
选择10个相关系数较高的波段进行模型的构建,分别为:R19,R31,R43,R49,R57,R58,R75,R155,R161,R167,其中,Ri(i=1,…,270)代表各波段对应的反射率,考虑到总磷浓度受多个变量的影响,故将这些波段同时作为变量进行逐步回归分析,建立多元线性回归模型,其基本思想是将变量逐个引入模型,进行F检验,对选入的变量逐个进行T检验,若检验表明回归效果显著,则引入回归方程,若回归效果不显著,则剔除作用不显著的变量,更新回归方程,这一过程反复迭代,直到没有不显著变量从回归方程中剔除,也没有显著变量引入为止。 实验最终筛选出3个显著变量,即3个敏感波段,分别为R19,R31,R43,多元回归模型为
Y=-149 835R19-5 965.82R31+83 337.6R43+62.859 5
其中,Y为浓度预测值,该模型的拟合度R2为0.975 27,均方根误差RMSE为3.544 7,表明该模型拟合效果良好。
3.1.2 基于CEM波段选择的总磷反演模型的构建
图4是利用CEM算法得到的各波段与总磷浓度矩阵的匹配程度,选择的匹配程度最高的波段信号R140。
最终通过显著性波段选择算法选择出6个具有代表性的波段,分别为R140,R80,R95,R161,R94,R131,同理将这些波段同时作为变量进行逐步回归分析,建立多元线性回归模型,最终筛选出3个敏感波段,分别为R95,R161,R131,多元回归模型为
Y=7 524.18R95+7 960.14R161-15 614.8R131+106.823
该模型的拟合度R2为0.866 899,均方根误差RMSE为8.223 54,表明该模型拟合效果较好。
3.1.3 总磷反演模型精度检验
前两小节分别利用PCC和基于CEM的波段选择算法(CEM-based Band Selection,CBS)两种方法对高光谱图像进行波段选择,然后利用选择好的波段进行建模,本小节对2种方法反演的模型进行精度检验,表1是3个检验样点在两种方法下的总磷浓度的反演值与实测值的对比,其中,相对误差为|(反演值-实测值)|/实测值。

表1 在2种方法下的总磷浓度的反演值与实测值的对比Table 1 Comparison of inversion values and measured values of TP concentration using two methods
由表1可知,利用CBS方法选择波段构造的反演的模型,虽然拟合度不高,但预测值更为准确,反演的浓度更接近实测值,相对误差最高为11.3%,最低为3.1%,平均相对误差为8.17%。
3.2 总氮含量的反演
同总磷,选择5个样点用于总氮反演模型的构建,另外3个样点用来检验模型的反演精度。
3.2.1 基于PCC波段选择的总氮反演模型的构建
将各波段的光谱反射率与总氮浓度进行皮尔逊相关性分析,如图5所示为总氮浓度与光谱反射率在不同波段处的相关程度。
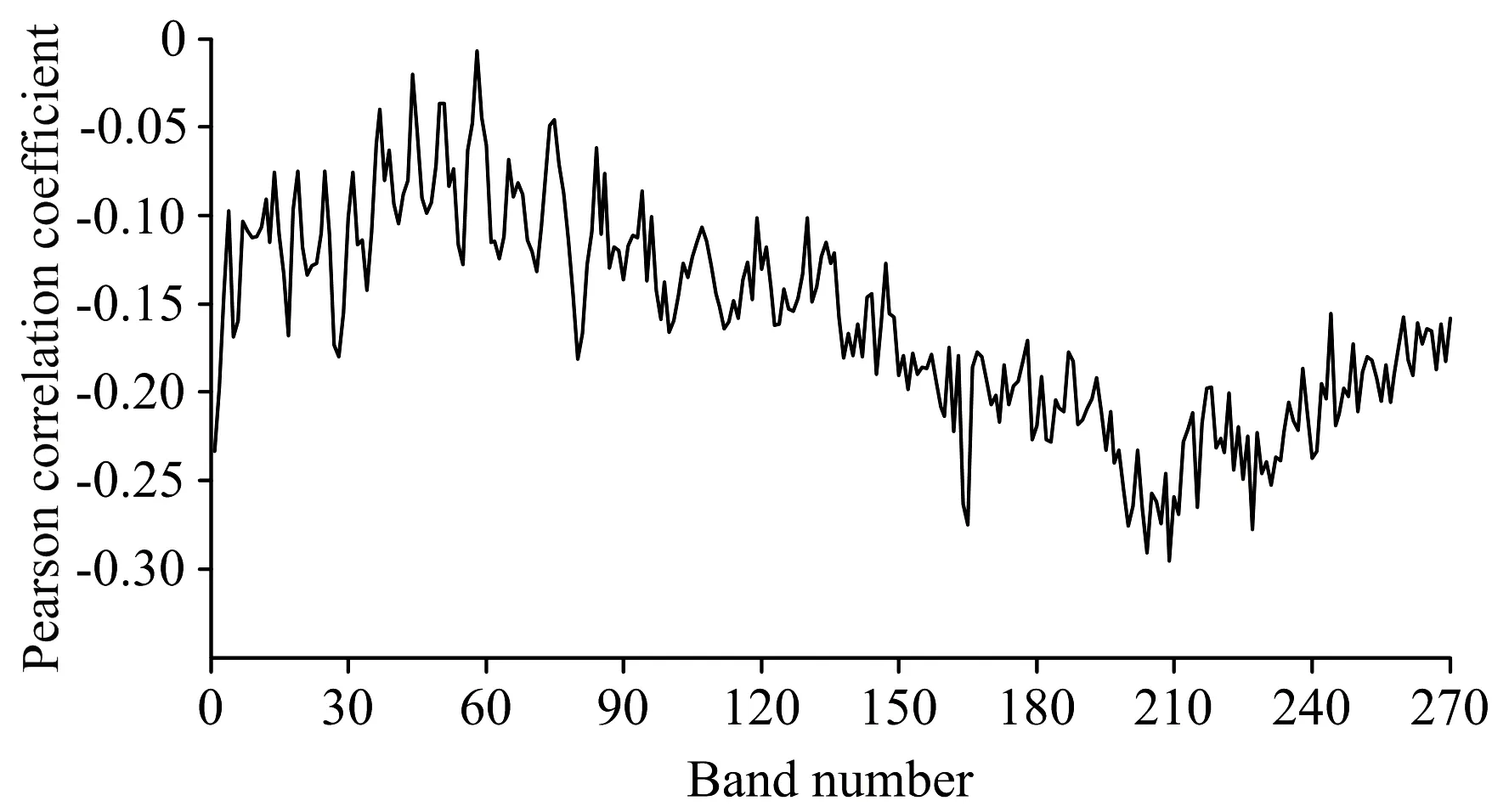
图5 总氮浓度与反射率在不同波段的相关程度Fig.5 Relevance between concentration of TNand reflectivity in different bands
选择10个相关系数较高的波段建模,这10个波段分别为:R164,R165,R200,R203,R204,R207,R209,R211,R215,R227,同理,这些波段同时作为变量进行逐步回归分析,建立多元线性回归模型,最终筛选出2个变量,即2个敏感波段,分别为R209,R215,多元回归模型为
Y=-1 300 870R209+1 453 550R215+898.555
该模型的拟合度R2为0.965 618,均方根误差RMSE为53.550 9,表明该模型拟合效果良好。
3.2.2 基于CEM波段选择的总氮反演模型的构建
图6是利用CEM算法得到的各波段与总氮浓度矩阵的匹配程度,选择的匹配程度最高的波段信号为R80。
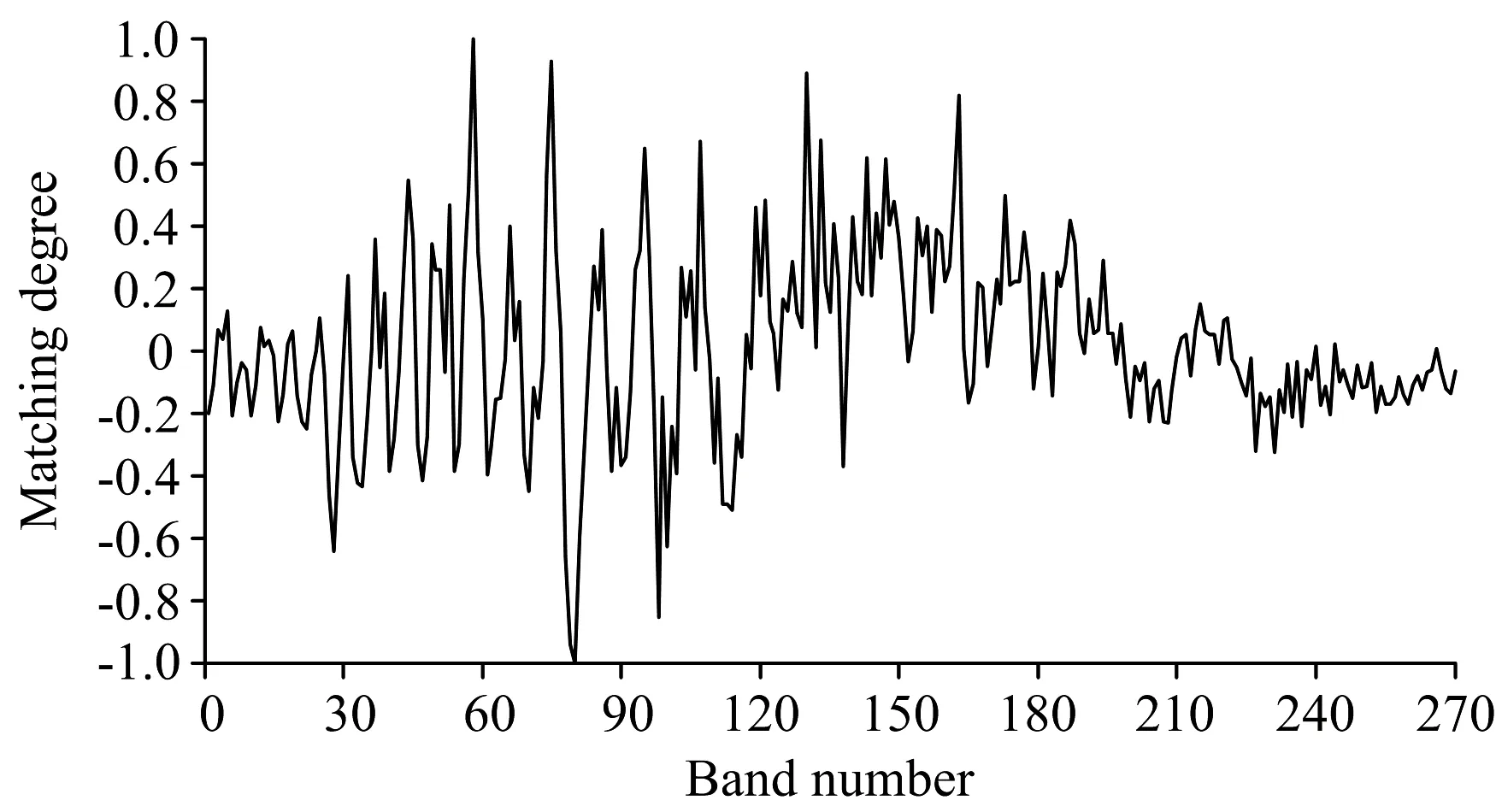
图6 各波段与总氮浓度矩阵的匹配程度Fig.6 Matching degree of each band withTN concentration matrix
最终通过显著性波段选择算法选择出6个具有代表性的波段,分别为R80,R58,R156,R95,R94,R78,同理将这些波段同时作为变量进行逐步回归分析,建立多元线性回归模型,最终筛选出3个敏感波段,分别为R80,R58,R156,多元回归模型为
Y=-158 206R80+115 568R58+98 478.1R156+1 048.31
该模型的拟合度R2为0.994 887,均方根误差RMSE为29.206,表明该模型拟合效果较好。
3.2.3 总氮反演模型精度检验
前两小节分别利用PCC和CBS两种方法对高光谱图像进行波段选择,然后利用选择好的波段进行建模,本小节对2种方法反演的模型进行精度检验,表2是3个检验样点在2种方法下的总氮浓度的反演值与实测值的对比。

表2 在2种方法下的总氮浓度的反演值与实测值的对比Table 2 Comparison of inversion values and measured values of TN concentration using two methods
由表2可知,利用CBS方法选择波段反演的模型更为准确,反演的浓度最接近实测值,相对误差最高为23.4%,最低为4.4%,平均相对误差为12.4%。
4 结 论
基于高光谱遥感数据,研究有效波段的选择方法,提出了一种基于CEM的浓度敏感波段选择方法,深入探讨分析了不同波段选择方法对氮磷浓度反演模型精度的影响。
(1)总磷含量的反演中,对比了PCC和CBS两种波段选择方法下反演模型的精度,利用CBS方法选择波段构造的反演模型,虽然拟合度不高,但预测值更为准确,平均相对误差为8.17%。
(2)总氮含量的反演中,利用CBS方法选择波段构造的反演模型,拟合效果优于PCC,且预测值也更为准确,平均相对误差为12.4%。
本工作的创新之处在于提出了基于CEM的浓度敏感波段选择方法,该方法能够最大程度地选择与浓度向量匹配度高且与已有波段向量冗余度低的波段,氮磷数据的分析比较表明了CBS的波段选择能力优于PCC,这一方法对高光谱数据的波段选择也具有一定的指导作用。
