基于虚拟光线再投影方法的激光吸收光谱燃烧场二维重建研究
2020-12-04那奕君黄孝龙翁春生
那奕君,李 宁,黄孝龙,翁春生
南京理工大学瞬态物理国家重点实验室,江苏 南京 210094
引 言
燃烧火焰的温度及其组分浓度是燃烧过程中非常重要的两个参数,表征了燃烧效率高低,发动机性能的优劣等[1]。 开展燃烧场温度和组分浓度的二维分布重建研究对提高燃烧效率,改良发动机设计等具有重要意义。 可调谐半导体激光吸收光谱技术(TDLAS)具有灵敏度高、响应速度快、可靠性和环境适应性强等优点,已经成功应用于气体温度、组分浓度等参数测量,并通过与CT技术相结合实现气体多参数二维重建。
代数迭代算法(ART)在不完全投影时依然能获得较好的重建结果因而被广泛用于研究燃烧场气体二维分布[2]。 例如美国弗吉尼亚理工大学Ma等[3]采用50 kHz测量频率,在垂直和水平方向分别布置15条光线对15×15网格J85航空发动机出口处300~2 300 K气体(H2O)温度进行了重建。 Xia等[4]提出两步迭代算法,采用5×6光线布置方法选取7 154.354/7 154.353 cm-1和7467.769 cm-1H2O吸收谱线对该重建算法进行了验证,结果表明在无噪声的情况下对于划分成11×11网格的单峰燃烧场重建误差小于0.1%。 Wang等[5]采用4个投影角度,每个投影角度6条光线的方式,测量了不同平面火焰温度和浓度分布,数值分析表明在吸收信号存在3%的噪声条件下仍可以得到重建结果。
在利用ART算法进行燃烧场二维重建时,目前主要存在的难点在于: (1)由于测量条件的限制,测量光线数量远少于测量区域网格数量,即投影数量远小于未知数数量,因此重建方程对应的矩阵条件数过大,如Ma等的对J85航空发动机进行测量的光线布置条件下方程条件数为8.6×1014。 (2)采用平行光线投影时,平行光线的角度存在较大限制,造成重建结果与待重建燃烧场存在较大偏差,如重建过程中将双峰燃烧场的重建为四峰燃烧场[6]。 (3)引入平滑处理机制[7]进行重建时,平滑因子选择不恰当也会引入较大误差。 由于针对不同的燃烧场模型平滑因子可选择的范围较大(0.01~0.1)[8],在此范围内不同的平滑因子对应的重建误差可能会相差10%,而平滑因子通常需要人为确定从而造成重建结果过多的受到主观因素的影响。
本文提出了针对有限投影数据的虚拟光线再投影二维重建算法。 利用差分虚拟光线实现病态方程组求解,通过多角度再投影方法解决差分过程相邻网格数据不连续等问题,减少重建过程中燃烧场先验信息的人为因素影响,提升燃烧场重建质量,具有重要理论研究意义和工程应用前景。
1 理论与方法
将探测区域f离散为n×n的网格,认为被测气体在每个方格内的温度和组分浓度均匀分布。 任意第i条光线穿过待测区域的第j个网格的长度为Lij。 根据Beer-Lambert定律,当波长为ν的光线i穿过测量区域时,气体吸收方程可以表示为式(1)[9]。 式中I0和It分别表示入射和透射的激光光强;P为气体总压;S(T)为谱线强度;X为待测气体体积浓度;L为光程;α为吸收率函数。 本文采用改进型ART(MAART)算法[10]进行重建。
(1)
当采用平行光线投影时,若光线间距大于网格间距时导致在投影方向上存在网格无光线穿过,将造成重建得到的ανi误差增大。 为降低该误差,通过差分法加入虚拟光线[11],如图1所示。
其中虚拟光线的投影值由相邻两边的实际光线的投影值进行差分运算得到
(2)

A(m+1)=HA(m)+A0
(3)
其中HA为作用于A的积分算子,A0为由差分虚拟光线法得到的投影值,A(m)表示第m次再投影后的光线投影值,利用A(m)求出第m次的重建结果并利用该结果再投影求出A(m+1)。 当H的2范数满足‖H‖<1,可以从理论上保证存在噪声时相应的重建结果是收敛和稳定的[12]。 计算流程如图2所示。

图1 虚拟光线法示意图Fig.1 Scheme of virtual beam method

图2 燃烧场重建算法流程图Fig.2 Reconstruction flowchart of the combustion field
2 重建结果分析
为了研究虚拟光线再投影方法在燃烧场二维重建中的可行性,对不同模型进行了数值仿真研究。 将重建区域离散为49×49的网格,包含气体温度和浓度共4 802个未知数,选取两条H2O特征吸收谱线(7 185.6,7 444.35 cm-1)。 为了衡量重建质量,定义温度和浓度归一化平均绝对误差Et和Ex。 其中T和X代表温度和浓度,orig和cal表示原始模型和重建结果。
(4)
2.1 相同投影数量条件下光路优化
为了研究光线分布对二维重建结果的影响,对多种实际光线以及再投影虚拟光线在燃烧场中分布方式进行分析研究。 测量燃烧场采用双Gauss分布,分布模型如图3所示。

图3双峰原始模型(a): 温度分布模型; (b): 浓度分布模型Fig.3 Bimodal original model(a): Temperature distribution model; (b): Concentration distribution model

图4 光线分布示意图(a): 方式A; (b): 方式B; (c): 方式C; (d): 方式DFig.4 Schematic diagram of beam arrangement(a): Mode A; (b): Mode B; (c): Mode C; (d): Mode D
针对49×49的离散网格区域,选择四种实际光线布置方式,分别为方式A实际光线成0°和90°各十条光线; 方式B实际光线成45°和135°各10条光线; 方式C实际光线成0°,60°和120°各7条光线; 方式D实际光线成0°,45°,90°和135°各5条光线。 对每个角度上实际光线进行差分获取虚拟光线投影数值,利用全部数据对燃烧场进行重建,重建误差如图5所示。 可以看出方式A和B的温度和浓度误差均大于方式C,造成这一结果的原因是A和B两种方式的光线投影角度过少,得到的有效数据较方式C少。 当实际光线数量为20条时,两角度投影重建结果可能无法准确反映燃烧场真实分布情况[7]。 方式D浓度重建误差相较方式C有明显增加,这是由于方式D投影角度多,但在每个投影角度上的光线数量偏少同时相邻平行光线之间的距离较大,经过差分运算后虚拟光线的投影值相较该位置实际投影值误差较大,在个别网格上会出现不同角度虚拟投影值之间相互矛盾,由于浓度重建对该矛盾更加敏感,所以方式D的浓度重建误差远大于方式C。 与其他方式相比,方式C通过增加投影角度抑制重建结果失真,同时每个投影角度合理的光线数量也减小了重建误差,保证了足够的空间分辨率。 由于以上原因,在本文之后计算过程中光线分布选择方式C。

图5 不同光线分布下的重建误差Fig.5 Reconstruction error for differentbeam arrangements
研究再投影角度对重建结果的影响。 对方式C进行再投影,第一组再投影角度选择45°,90°和135°,第二组再投影角度选择30°,90°和150°。 如图6所示,重建误差都随着重建次数增加而减少,十次以后趋于稳定。 第二组分布方式Et的减少量是第一组的82.5%,Ex的减少量是第一组53.8%。 分析其原因,由于网格划分为正方形划分方式,第一组分布方式虚拟光线经过每个网格路程分布更为均匀,在迭代运算过程中网格参数所占比重更为合理。

图6 重建误差的变化趋势(a): Ex随再投影次数的变化趋势; (b): Et随再投影次数的变化趋势Fig.6 Variation trend of Reconstruction error(a): Ex variation for reprojection number; (b): Et variation for reprojection number
2.2 算法对比
选取采用平滑处理机制的ART算法与本文算法进行比较分析。 当实际光线数目远小于待测区域网格数目时,采用平滑处理机制的ART算法只会对部分网格中的气体参数进行迭代,其余网格中的气体参数只能通过平滑处理机制获得。 当平滑因子选为0.02时,重建结果温度和浓度误差最小,Et和Ex分别为9.88%和11.91%。 运用本文重建算法并设置再投影次数为10次,重建误差Et和Ex分别为3.77%和8.26%,如图7所示。 网格划分较细但测量光线数量不足时,采用平滑处理机制ART算法只能大致描绘出燃烧场温度轮廓。 采用虚拟光线法能够有效解决没有测量光线经过网格时导致重建偏差较大的问题,当进行再投影重建后相邻网格温度不连续的情况得到有效改善,重建结果更接近原始燃烧场模型。
2.3 重建结果分析
为了研究重建算法在实际测量条件下重建效果,对光线投影数值加入0.5%随机噪声,得到的重建结果由图8给出。 温度场与浓度场重建误差最大值都出现在峰值位置附近,温度最大相对误差9.24%,浓度最大相对误差19.13%。 得到重建误差随着再投影重建次数的变化规律由图9给出。 随着再投影运算次数的增加,Et与Ex都呈现出下降趋势并最终保持稳定,经过十次再投影重建后Et减少到3.55%,Ex减少到8.44%。

图7 不同算法的温度场重建结果(a): 采用平滑机制的ART算法; (b): 虚拟光线再投影法Fig.7 Reconstruction temperature field for different algorithms(a): ART witi smoothing mechanism; (b): Virtual beam and re-projection method
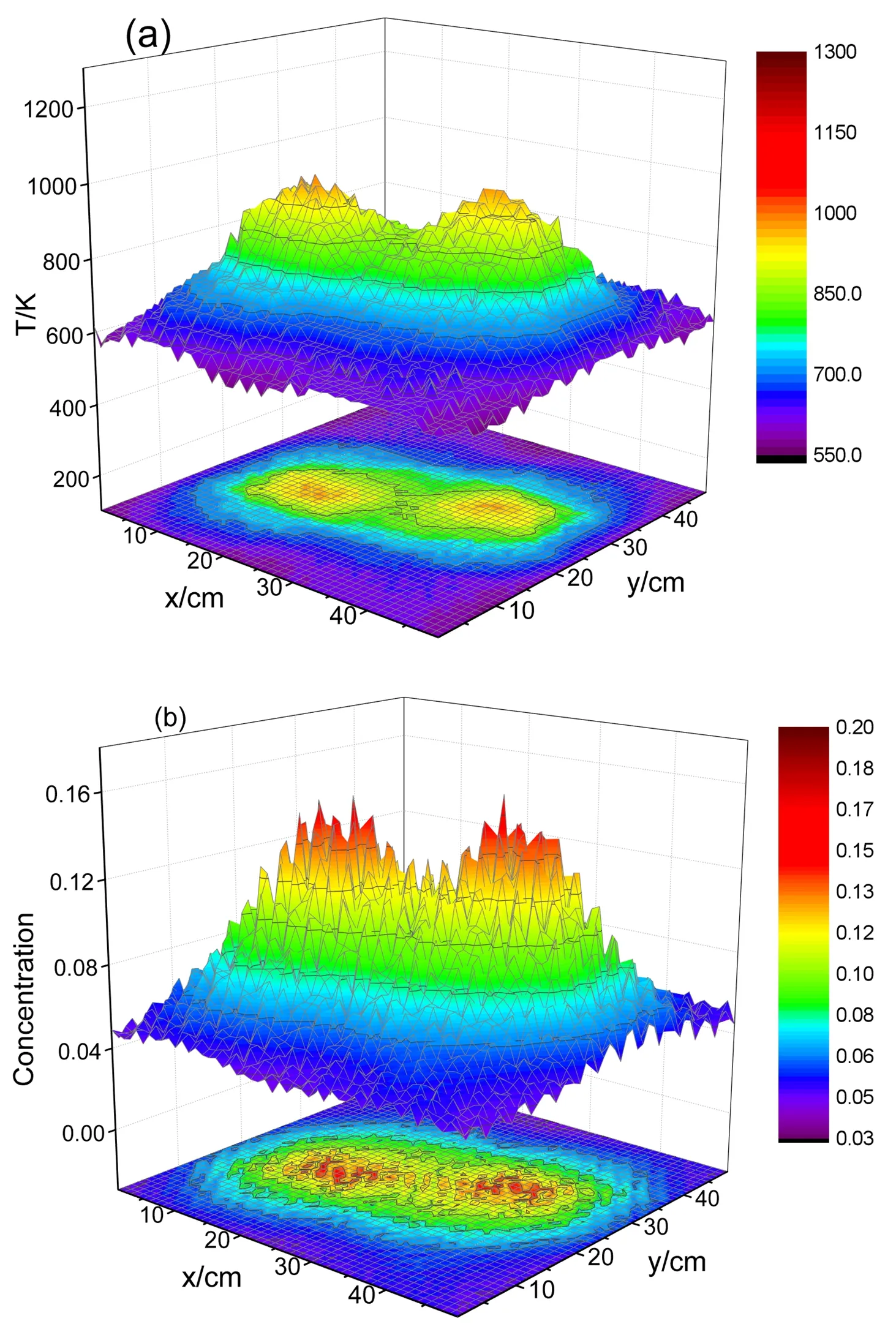
图8 双峰燃烧场重建结果(a): 温度场重建结果; (b): 浓度场重建结果Fig.8 Reconstruction result for bimodal combustion field(a): Reconstruction temperature field; (b): Reconstruction concentration field

图9 含0.5%噪声时重建误差的变化趋势Fig.9 Variation trend of Reconstructionerror with 0.5% noise

图10 随机噪声对重建误差的影响Fig.10 Effect of random noise onreconstruction error
为了研究不同幅值噪声对重建结果的影响,对实际光线分别添加0.5%,1%,2%和5%随机噪声并对重建结果进行研究。 再投影10次时重建误差如图10所示。 当噪声不超过5%时,浓度重建误差与温度重建误差均随着噪声的增大而增加,温度重建误差增加幅度更为明显。
2.4 不同模型下重建结果分析
为了验证本文重建方法的通用性,选取多峰燃烧场进行重建分析。 设置温度如图11所示的三峰燃烧场,温度范围600~1 134 K,H2O浓度范围5%~18.34%。 燃烧场三个温度峰值分别为1 134,1 006和937 K,浓度峰值为18.34%,15.16%和13.43%。 对实际光线投影值添加0.5%的随机噪声,十次再投影重建后Et为7.05%,Ex为15.11%。 图12为温度重建结果。
通过图12可以看出,多峰燃烧场的重建质量有所降低,重建误差增大,但重建结果依然可以展现出燃烧场的主要特征,峰值位置、峰值数量等均未出现明显失真。 结果表明当燃烧场较为复杂时,本文重建方法依然可以提供有效的燃烧诊断信息,适用于温度组分参数连续变化的燃烧场诊断分析。
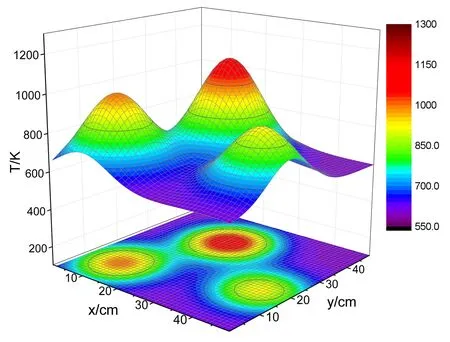
图11 三峰温度分布模型Fig.11 Multimodal temperature distribution model

图12 三峰温度重建结果Fig.12 Multimodal temperature reconstruction results
3 结 论
基于激光吸收光谱技术采用修正的自适应代数迭代算法对燃烧场温度分布进行二维重建。 为了实现在入射光线较少情况下对被测区域的细致刻画,提出了一种基于虚拟光线与再投影方法的燃烧场二维重建方法。 该方法将虚拟光线与再投影技术相结合,实现了燃烧场温度组分浓度的二维重建,无需对燃烧场先验信息进行人为调整,提升了重建质量。 通过对比不同方法的重建结果,该方法的重建结果对燃烧场的重建更为准确,当测量投影含有1%的随机误差时,温度重建误差为3.59%,浓度重建误差为8.75%。 对于不同燃烧场模型,该方法依然能准确的重建出燃烧场峰值的位置以及峰值大小,不出现明显失真。 结果表明该方法能有效对二维燃烧场进行更为细致的重建。
