极限位姿工况下四自由度机械手力学特性

秦建华, 蒋芳明,2

(1.桂林理工大学 机械与控制工程学院，广西 桂林 541006;2.桂林理工大学 南宁分校，南宁 530001)

0 引 言

随着机器人技术的日益进步, 工业机器人已经广泛应用于工业生产制造业中, 代替人力从事重复性高、 危险性强的劳动。 在复杂环境下, 机械手负荷工作易发生弯曲、 扭转等变形, 严重时甚至出现断裂现象[1-3]。 由于使用频率较高、 承载质量大、 使用条件恶劣、 工作过程中时常达到极限位姿等, 四自由度机械手的整体性能直接受到影响。 机械手的结构分析对提高机械手整体性能水平具有重要的意义。Kozyrev等[4]对Isoglide型并联机械手的强度与刚度特性进行了测试,通过分析其力学特性改进了并联机械手的结构,并获得了较好的效果；孙龙飞等[5]采用平行四边形边框架及电动缸对角驱动的桁架结构设计了新型5自由度工业机械手,并验证了该机械手的刚度特性；文献[6]对码垛机器人进行动力学分析,并对3种不同姿态下的机器手进行模态分析；刚度反映了机械手变形与外部载荷之间的映射关系,刚度的高低可直接影响到机械手末端执行机构的定位精度,从而导致机械手产生执行误差[7-10]。但上述文献均是在常态位姿工况下对工业机器人进行力学特性研究,对非常态位姿工况下力学特性的研究较少。

基于此,本文建立了机械手的有限元模型,并在水平最大伸展位姿与垂直最大伸展位姿工况下进行了仿真实验,得出机械手的静态应力与应变数据,并进行物理样机实验的对比,验证结果的有效性,研究结果可为极限位姿状态下机械手的设计和制造提供参考。

1 有限元模型的建立

1.1 几何模型的建立与简化

以某型四自由度的工业机械手为研究对象,机械手主要由固定基座、旋转臂、大臂、小臂、前臂等部分组成。旋转臂、前臂的旋转运动以及大臂、小臂的俯仰运动构成该机械手的自由度分布。机械手材料参数见表1。

表1 机械手材料参数Table 1 Material parameters of manipulator

采用Pro/E软件对实体进行几何建模。由于本文主要研究位姿的变化对机械手主要构件的力学影响,建模时需要对实体模型进行一定的简化处理,如前臂与小臂处的电动缸,各连接处的孔、圆角、凸台等非承载的构件,虽然孔等形状特征会产生应力集中现象,但对机械手主要部件的力学特性影响较小,而电动缸等具有质量的驱动构件,在模型简化时以材料参数进行修正,故可对上述构件进行简化处理。几何实体简化模型如图1所示,建立后将其导入ANSYS软件。

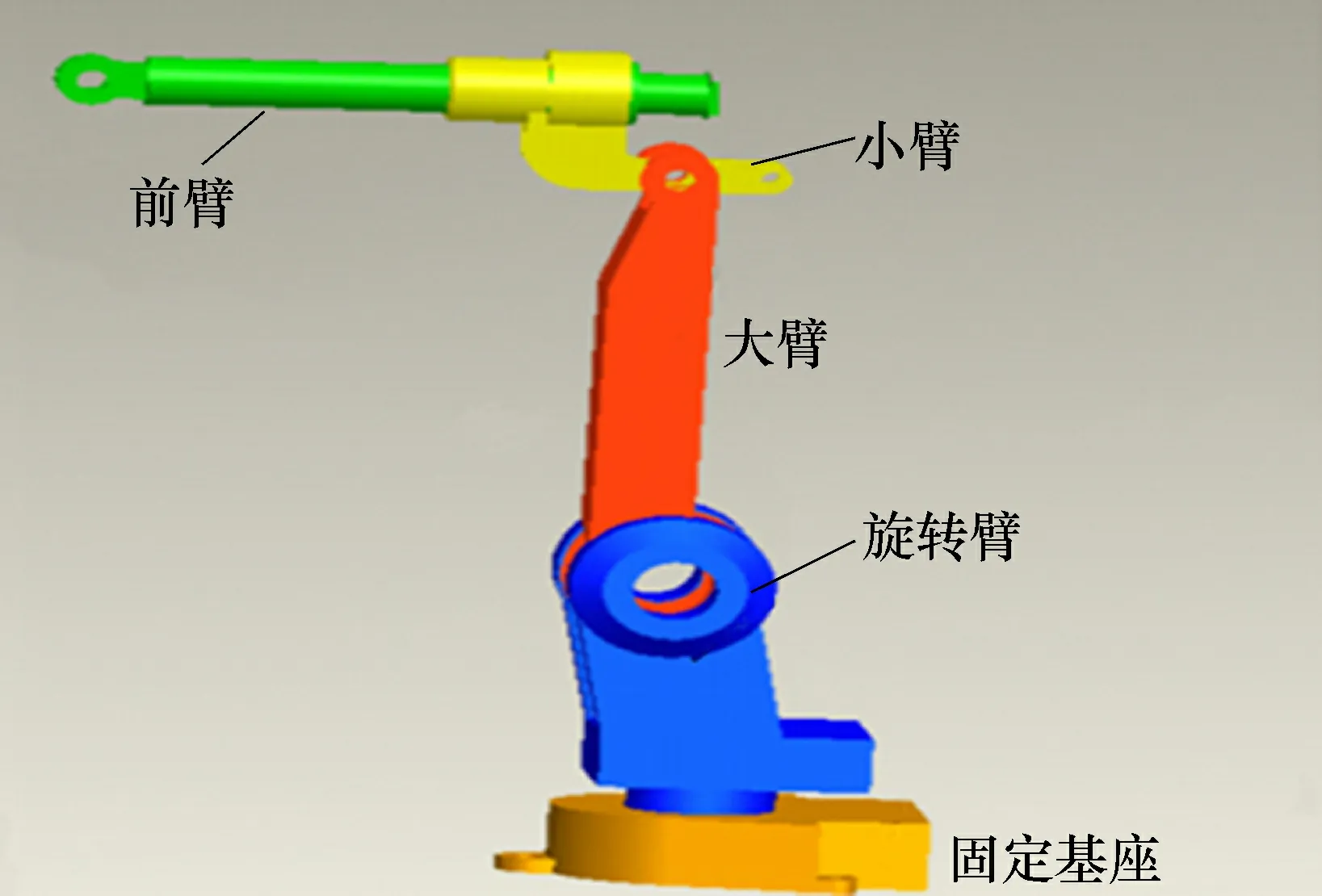
图1 四自由度工业机械手几何简化模型Fig.1 Geometric-simplified model of 4-DOF industial manipulator

1.2 网格划分

由于机械手的三维实体模型较为复杂,且形状不规则,需要从Pro/E 4.0中导入,在网格划分选择范围内可选择六面体单元或四面体单元,而Solid187单元(二次四面体单元)具有二次位移型插值函数,因此该模型更适合采用Solid187单元进行网格划分。划分完成后机械手的水平和垂直方向有限元模型和模型节点如图2所示。

图2 极限位姿下机械手的网格划分Fig.2 Meshing of manipulator in extreme poses

1.3 约束与载荷的施加

工作时机械手与其他部件发生接触并产生载荷与约束。因此, 有限元模型建立时, 应充分考虑其他部件对其应力影响,在施加约束与载荷之后,在相应的铰接点与受力位置处建立刚性区域[11-13],如图3所示。

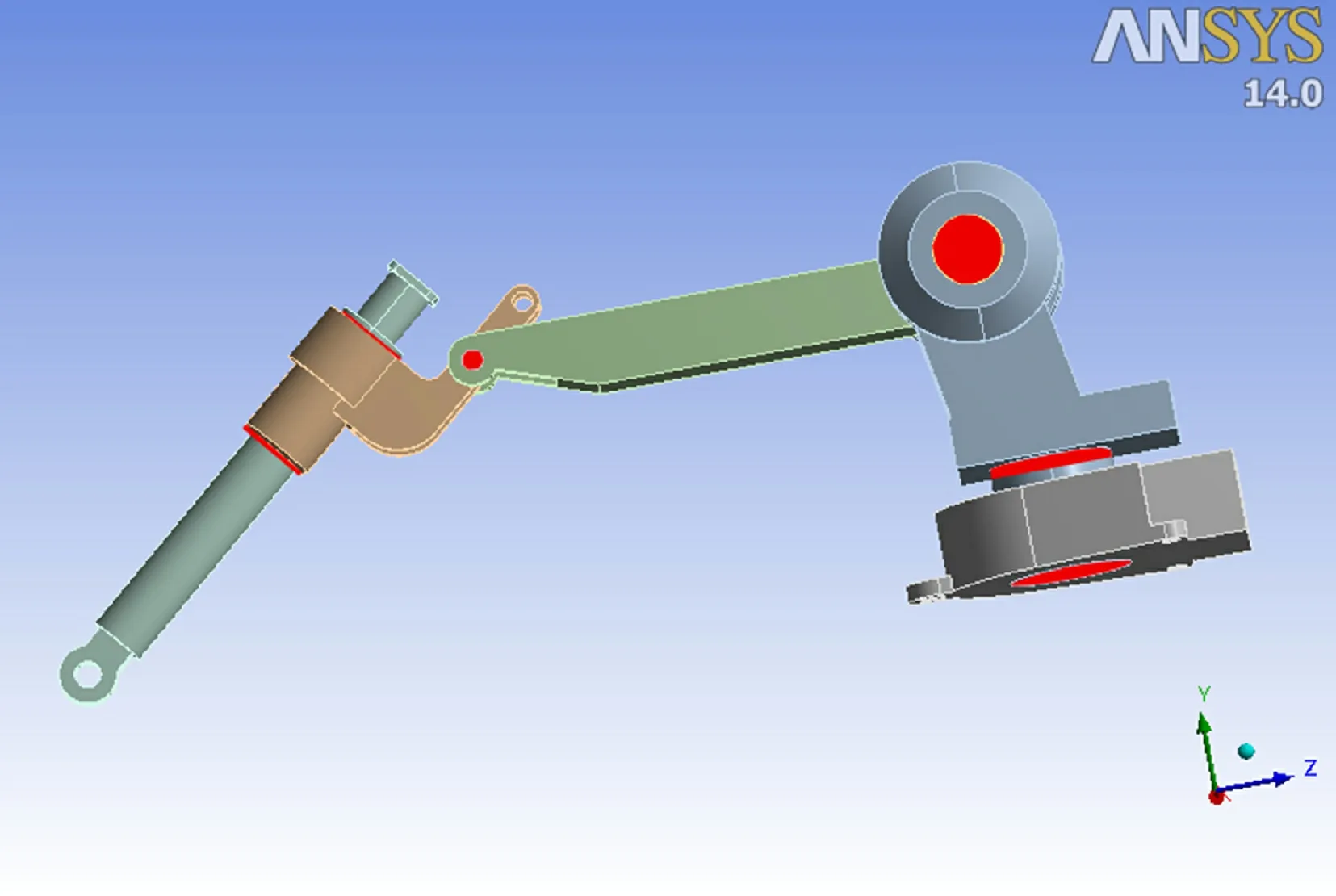
图3 四自由度工业机械手刚性区域图Fig.3 Rigid area diagram of 4-DOF industial manipulator

2 极限位姿工况下机械手的仿真实验

2.1 水平最大伸展位姿工况

水平最大伸展位姿工况下,在机械手前臂前端处施加200 N的重力,以此模拟机械手抓取20 kg重物时的工况。机械手相应节点的水平最大伸展位姿工况下等效应力和位移云图如图4所示。

水平最大伸展位姿时机械手的应力分布(图4a)是从小臂连接杆向外扩张, 最大等效应力出现在小臂的连接杆上端, 最大等效应力为21.904 MPa; 水平最大伸展位姿时变形最大的位置位于机械手前臂的最前端(图4b), 最大变形约为0.298 mm。

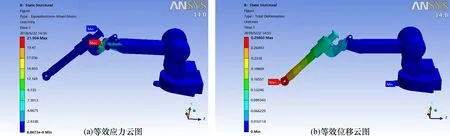
图4 水平最大伸展位姿下机械手的有限元静态仿真实验Fig.4 Finite element static simulation experiment of the manipulator in horizontal maximum extended posture

2.2 垂直最大伸展位置工况

相同负载工况下,整个机械手受竖直向下的重力,以垂直最大伸展位姿进行工作。机械手垂直最大伸展位姿的等效应力和位移云图如图5所示。

垂直最大伸展位姿的应力分布(图5a)主要是从小臂的连接杆处向外扩张, 最大应力为6.919 9 MPa;机械手的垂直最大位姿时变形最大处在机械手的最前端(图5b), 约为0.094 7 mm。

图5 垂直最大伸展位姿下机械手的有限元静态仿真实验Fig.5 Finite element static simulation experiment of the manipulator in vertical maximum extension posture

综上,负载为200 N的机械手正常作业时其各部件静态分析结果表明:水平位姿工况下的最大应力与形变的数值约为垂直位姿工况下的最大应力与形变数值的3倍,因此应尽量避免出现机械手水平最大伸展位姿的工作状态。由于机械手在工作时承受的静载荷所造成的应力值都比较小,而机械手材料的屈服极限均大于30 MPa，且小于Q235钢的屈服极限235 MPa,根据第四强度理论,两种状态下的机械手均能满足工作要求。所以该机械手设计满足静刚度和静强度要求。

3 四自由度机械手应力测试与结果

3.1 测试方案

为了验证极限位姿工况下机械手仿真实验的有效性,对机械手关键处的应力进行测试。应变片粘贴位置位于机械手表面区域,由于机械手在载荷的作用下仍处于平衡状态,因此可在表面区域粘贴由4个应变计组成的应变花,具体贴片分布如图6所示。

图6 机械手应力测点分布Fig.6 Distribution of stress measurement points of the manipulator

极限位姿工况下,对机械手进行负载应力测试,先将扭力电机连接前臂前端以施加载荷,控制扭力电机缓慢施加扭矩,力矩施加原则为从0开始缓慢增加至额定力矩,待机械手稳定后又缓慢卸载至初始状态,载荷加载过程重复3～6次,观察应变片的变化,并记录实验结果。

3.2 测试结果及分析

采用NI仪器PXI进行测量,各测点的应力测试值如表2所示。其中对每个测点测量3～6次,并取其最大应变的平均值。而各测点的单向应力为

表2 测点应力测试结果Table 2 Stress test results of measuring points

σ=Eε,

式中:E为弹性模量;ε为应变最大值;σ为应力值。

形变分析:由于机械手的装载位置位于机械手前臂的前端,因此两种位姿的最大变形位置处于前臂的负载位置范围内。

应力分析:水平最大伸展位姿工况下,机械手前臂主要受拉力的影响,小臂受拉力和弯矩的组合力,弯矩线性增加,在旋转臂处达到最大值,且应力数值会受到材料截面面积的影响。因此,应力趋势呈缓慢地增加然后下降从关节处延伸至大臂。同理,垂直最大伸展位姿工况的机械手小臂主要受压力与弯矩的组合力,但由于此位姿主要受压力作用,而弯矩增长幅度较慢。因此,两者的应力趋势大体相似,然而由于弯矩的差异,导致应力值存在明显差异。

有限元分析的数值结果与在两种姿势条件下工作的机械手表面应力的测量数值结果的比较,如图7所示。所有测点的应力相对误差均处于10%～26.7%范围内, 且相对误差较大的测点在整个测点中所占的比例较小, 因此对数据分析影响不大。 基于上述分析, 测量点的相对误差在工程允许范围内, 属于偶然误差。 从总体上看,在载荷加载过程中,机械手没有发生断裂,实验结果与仿真结果趋势一致,数值基本相当,验证了机械手有限元建模的合理性与有限元分析的正确性。

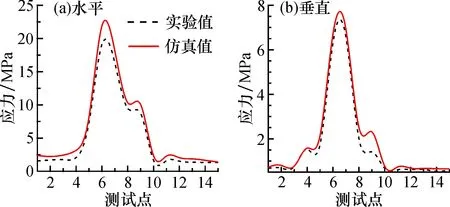
图7 极限位姿工况实验数据与仿真数据对比Fig.7 Comparison of experimental data and simulation data in extreme poses

4 结 论

本文建立了四自由度机械手有限元模型,并分析了典型机械手处于两种极限位姿工况下的应力与形变分布规律,两者最大应力均发生在小臂连杆上端处,最大位移发生在前臂负载最前端。为确保仿真实验的有效性,进一步根据有限元计算分析结果对机械手强度薄弱部位展开贴片应力测试,并将有限元仿真结果与实验结果进行了对比研究,结果表明:在水平位姿工况下机械手的最大应力为19.131 MPa,最大位移为0.278 mm;在垂直位姿工况下机械手的最大应力为6.577 MPa,最大位移为0.086 mm。仿真结果与实验结果基本吻合,从而验证了四自由度机械手有限元分析的正确性,为极限位姿工况下机械手在实际应用中提供了一定的强度参考指标。