基于改进人工蜂群BP神经网络的PM2.5浓度预测模型

胡俊,杨辉军,程晨

安徽国际商务职业学院 信息工程学院，安徽 合肥 231131

0 引言

工业的迅猛发展造成废气、废水及废弃物等污染物的排放量日益上升，大气污染程度加剧。对大气污染及人类健康影响最严重的是细颗粒物质(particulate matter，PM)，它们既影响人们的生活与出行，又破坏生态系统的平衡性。PM2.5的浓度直接关系人类日死亡率的上升与疾病症状(如哮喘、支气管炎及肺功能衰弱等的增加)。因此PM2.5浓度问题引发各界人士的高度关注，预测PM2.5浓度成为热点研究课题。

文献[1]提出基于多模态支持向量回归混合预测模型，通过集成经验模态分解方法划分每天的PM2.5浓度均值，利用所得的各频段分量序列提升数据平稳性，基于各分量的独有属性，完成不同的支持向量回归模型设计，明确每组分量的输入变量，根据叠加的分量预测值获取预测结果；文献[2]通过时间尺度重构改进集成经验模态分解法-广义回归神经网络模型，根据PM2.5浓度的时间序列数据，探析浓度的多尺度变化属性与气象因子、大气污染因子的尺度响应特征，取得预测浓度；文献[3]设计基于T-S模糊神经网络的PM2.5浓度预测方法，依据测得的实际数据，采用偏最小二乘法选取有关PM2.5的辅助变量，利用T-S模糊神经网络，构建浓度与变量间的软测量模型，通过历史数据实现模型训练。

上述预测模型因大气污染的影响因素较多，预测结果出现了高度的非线性情况，产生较大偏差。本文创建基于改进人工蜂群BP神经网络的PM2.5浓度预测模型，以期提供更为精准的预测结果。

1 人工蜂群BP神经网络算法改进

1.1 人工蜂群算法的改进

人工蜂群反向传播(back propagation，BP)神经网络善于处理非线性数据或存在噪音的数据，尤其是特征问题具有模糊性、不完整性及不严密性等特点时，该方法的处理效果十分显著，广泛应用于优化控制、智能决策、模式识别及预测预报等问题研究中。

以搜索形式与跟随蜂选择概率为改进角度，对人工蜂群算法进行寻优精度与收敛速率的提升。雇佣蜂[4-6]与跟随蜂在原有食物源周边的随机搜索式为：

(1)

式中：i为食物源的编号，i∈[1，SN],其中SN为食物源数；j为问题解向量中分量参数的编号，j∈[1，D],其中D为问题的维数；Xij为局部最优路径；r1、r2为随机数，分布区间分别为(0，1.0)、(0，1.5)；Xne,j为跟随蜂在原有食物源周边的搜索路径；yj为全局最优解的第j个变量。

式(1)可大概率避免出现局部最优情况，但其搜索的随机性减缓了算法的收敛速度[7-9]。为了提高收敛速度，在搜索过程中引入全局最优解。但添加全局最优解会破坏蜂群的多样性，因为蜂群适应度较高，食物源集中速度过快，导致收敛过早，陷入局部极小值。加入自适应调整因子b1与b2，平衡收敛速率与种群多样性。改进的人工蜂群算法公式为：

(2)

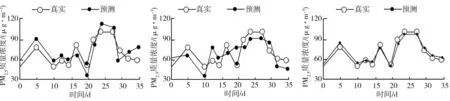
根据式(2)可知：算法的初期阶段，b2>b1，所选食物源向全局最优解的集中速率相对更快，收敛速度提升；后期阶段，b2

为了改进算法后期阶段中局部最优解对搜索性能的抑制，可以增强随机食物源的影响力，提高种群的多样性。

传统人工蜂群算法中，跟随蜂选取食物源的概率

(3)

式中fi、fj为Xi、Xj对应的适应度。

由式(3)可知：食物源的选中概率随适应度的升高而增大，因进化阶段内蜂群向较高适应度的食物源迅速聚拢，破坏种群多样性，陷入局部极小化。采用反向轮盘赌[13-15]选择机制，式(3)改写为：

(4)

该机制让跟随蜂开采适应度较差的食物源，避免种群向高适应度食物源聚拢，维持种群适应度，但算法前期阶段的收敛速率下降。为了确保种群多样性，不再发生局部最优状况，跟随蜂在算法前期向高适应度食物源集中，在算法后期向低适应度食物源集中。

引入自适应判断因子

经过优化的概率计算公式为：

(5)

式中:rand为区间[0，1]内的任意值；σ为变量，与niter正相关，在算法的前期阶段，种群选取式(3)计算选择概率的可能性较大，但后期阶段极有可能选取式(4)计算选择概率。

1.2 人工蜂群下BP神经网络的改进

BP神经网络是一种基于梯度下降法[16-18]的多层网络模型，将初始权重与阈值赋予网络后，利用层间前向传输信息并计算网络的输出值，采用期望输出与实际输出形成的偏差，利用误差反向传播，调整网络的权重与阈值，通过不停地训练、对比，最小化算法的仿真偏差[19-22]。

由人工蜂群算法处理BP神经网络权重的更新阶段，加快收敛速度，防止出现局部极小值状况。步骤为：1)按照输入样本和输出要求，构建神经网络结构。2)权重wij与输入层和隐藏层相连，权重wjk与隐藏层和输出层相连，在初始化BP神经网络后，将人工蜂群算法的优化目标设为wij与wjk。3)初始化人工蜂群算法的蜂群规模、nmax及nlimit等参数。4)实施跟随蜂、雇佣蜂及侦查蜂的操作，寻求最佳食物源。5)把最佳食物源传回BP神经网络。

2 PM2.5浓度预测模型设计

2.1 灰色关联探析

基于灰色系统理论，当系统存在已知信息或者不确定信息时，其数据可能出现随机性，但仍具有一定的有界性与有序性，属于一种规律性数据集。PM2.5的质量浓度受多种因素的影响，所有因素之间的关联性不仅无法定量分析，而且在特定区域中动态变化。采用灰色关联分析[23-25]策略甄别所有因素间的发展趋势依赖程度，探索PM2.5质量浓度所有影响因素的影响程度。

1)构建初始数据矩阵

xi=[xi(1)xi(2)xi(3) …xi(k)]，

式中xi(k)为第k时刻第i因素的初始数据，其中i=1,2,…,7，k=1,2,…,n，n为初始数据的长度。

2)求解xi的变换矩阵

3)计算差序列

4)求解关联系数

式中：φ为分辨系数，主要用以实现关联系数之间差异显著性的提升，其取值范围是(0，1)。

5)求解灰色关联度

由于PM10、NO2、CO、O3、SO2的浓度、温度以及相对湿度具有较大的关联性，灰色关联分析策略将其作为PM2.5质量浓度的主要影响因素，并设为预测模型的变量因子。

2.2 PM2.5数据处理

若把采集的PM2.5样本数据直接用于改进人工蜂群BP神经网络的预测模型中，预测结果偏差将大幅增加，因此需要对所得数据进行预处理。

采集的样本数据取值范围较大，采用三倍标准差方法检验处理所采集的样本数据，滤除异常数据。三倍标准差方法的基本原理为：假设X1，X2，…,Xi，…，Xn为所有的样本数据集合，其平均值与标准差公式为：

在样本数据的检验阶段，若数据的标准差大于3γ，则该数据是异常数据，需去除。

为了同一数据的量纲与量级，缩小取值差异性，利用最大最小线性归一化策略归一化处理所得样本数据，归一化公式为：

式中：Xnorm为归一化处理后的样本数据，Xmin、Xmax分别为相应属性的极小值与极大值，X为当前待归一化处理的样本数据。

根据污染等级，利用三位二进制编码标签化样本数据：001为优，010为良，011为轻度污染，100为中度污染，101为重度污染，110为严重污染。

2.3 PM2.5浓度预测模型的实现

对wij、wjk及隐藏层阈值a和输出层阈值c进行初始化处理，基于输入值x1,x2,…,xi、wij与a，求解隐藏层输出值

式中：l为BP神经网络的隐藏层节点个数，f为激励函数。

依据求解的每个Hj、wjh及ch，计算所有输出层PM2.5质量浓度

计算Yh和PM2.5预估质量浓度Yh′的误差

更新神经网络的权重与阈值后，依据eh，调整wij、wjh、各隐藏层aj和各输出层ch为：

wjh=wjh+ηHjeh，

ch=ch+eh,

式中η为神经网络的学习速率。

待所得数值满足终止条件时，预测结束；否则，重新计算隐藏层与输出层的数值，再次调整网络的权重与阈值，直到符合终止条件。

3 仿真分析

3.1 仿真环境

图1 BP神经网络框架示意图

采用Matlab编写仿真分析的代码，BP神经网络含有输入层、输出层及隐藏层，各层级间的神经元相互连接，层内的神经元不相连，如图1所示。

将BP神经网络输入层、隐藏层以及输出层的节点神经元数量分别设置为8、18和2，得到待优化的200个BP神经网络优化参数指标，包括BP神经网络阈值20个，权重180个，其中含有144个输入层与隐藏层间的权重，36个输出层与隐藏层间的权重。人工蜂群算法的指标参数设定为：种群规模为100，最多滞留10次，迭代次数不超过50次，搜索步长是0.5，学习因子为2。

在中国环境检测网站发布的实时数据中，选取100组PM2.5质量浓度数据作为训练样本与预测检验数据。

3.2 性能对比分析

为了验证本文模型的精准度，分别采用文献[1-2]中的模型进行仿真分析，如图2所示。

a)文献[1]模型 b)文献[2]模型 c)所建模型图2 PM2.5浓度预测模型效果对比

由图2可知：采用文献[1-2]模型预测35 d内的PM2.5质量浓度与真实浓度存在一定差异，采用本文基于改进人工蜂群BP神经网络的PM2.5浓度预测模型得到的预测质量浓度与真实质量浓度非常接近，说明所建模型的预测准确度较高。

求解采用不同方法预测PM2.5质量浓度的均方误差。均方误差可评价数据的变化程度，是预测浓度与真实之差的平方和的平均值，该值越小表明预测结果的准确度越高，其计算公式为：

(6)

利用式(6)得到不同模型的预测质量浓度的相对误差，如表1所示。

通过表1可以看出：文献[1-2]及本文模型的相对误差分别为27%、19%和8%，其中，文献[1]模型的最大和最小相对误差分别为0.03、0.99，文献[2]模型的最大、最小相对误差分别为0.05、0.28，而本文模型的最大和最小相对误差分别为0.01、0.15，与其他两种模型相比，本文模型的相对误差下降幅度较大，误差极小，准确性较高。

4 结语

本文提出基于改进人工蜂群BP神经网络的PM2.5浓度预测模型， 引入全局最优解与自适应调整因子，使收敛速率与种群多样性得以平衡，依据灰色关联分析策略，确定预测模型的变量因子，基于神经网络的预测浓度与真实浓度形成的误差，实现权重与阈值的重新调整，完成预测模型的创建。仿真结果表明：该模型的预测准确度较高，预测浓度的相对误差较小，为大气污染预控提供了有效的技术支持，具有重要的现实意义与实践价值。

表1 各模型PM2.5预测质量浓度与实际质量浓度的相对误差