制动工况下车轮不圆对车辆动力学性能的影响

兰清群，宋福

1.安徽交通职业技术学院，安徽 合肥 230051；2.深圳地铁运营集团有限公司，广东 深圳 518000

0 引言

车轮不圆是指具有制造缺陷、车轮磨耗或者车轮镟修时产生的相关缺陷，车轮不圆通常导致车轮与轨道之间的垂向力明显增加，改变轮轨间的动态响应，从而影响车辆的稳定性和安全性以及轮轨系统部件的使用寿命。文献[1-3]对有不圆缺陷的车轮的轮轨力进行了仿真分析及试验研究。有不圆缺陷的车轮对轨道和列车的影响已有实例证明[4-6]，并已通过刚体和柔体动力学进行了研究[7-10]。文献[11-13]通过分析轮轨关系，对周期性车轮不圆(车轮的不圆磨耗类似多边形形状，假设缺陷沿着车轮圆周均匀分布)的形成机理进行了详细研究。文献[14-18]就恒速下车轮不圆缺陷对轮轨的动力学影响进行了研究。文献[19-23]研究了列车车轮缺陷对轮轨的垂向动力学响应。但在制动工况下车轮不圆对车辆动力学影响的相关研究较少。文献[24]对制动工况下车辆的动力学性能进行了分析，但未考虑缺陷车轮的影响。

本文基于多体动力学模型，对常用制动和紧急制动工况下装有不圆缺陷车轮的车辆系统动力学性能进行仿真分析。

1 模型建立及验证

1.1 多体动力学模型

车辆-轨道系统多体动力学模型如图1所示，在施加制动转矩之前，由2个转向架构架和4个轮对(1根车轴和2个车轮组成1个轮对)组成的多体车辆系统以恒定速度运行。该模型中，每个部件均定义为6个自由度，分别为沿x、y、z轴3个方向的线性运动和围绕x、y、z轴3个方向的旋转运动。轨道为刚性，轮对通过轮/轨法向接触力与钢轨耦合。图1中：mb为车体质量，mb=30 000 kg；mf为构架质量，mf=2500 kg；mw为轮对质量，mw=1120 kg；Kpx、Kpy、Kpz分别为一系悬挂(轴箱与构架之间的减振装置)纵向、横向、垂向刚度，Kpx=Kpy=Kpz=4 MN/m；Ksx、Ksy、Ksz分别为二系悬挂(构架与车体底架之间的减振装置)纵向、横向、垂向刚度，Ksx=Ksy=0.4 MN/m，Ksz=0.3 MN/m；Cpx、Cpy、Cpz分别为一系悬挂纵向、横向、垂向阻尼，Cpx=Cpy=80 kNs/m，Cpz=25 kNs/m；Csx、Csy、Csz分别为二系悬挂纵向、横向、垂向阻尼，Csx=Csy=Csz=10 kNs/m。

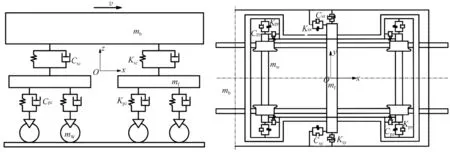
a)主视图 b)俯视图图1 固定坐标系中的车辆-轨道系统多体动力学模型

同时，建立车辆-轨道系统动力学模型时需要输入的参数还有：轮对纵向惯性矩为100 kg·m2，轮对垂向惯性矩为420 kg·m2，构架纵向惯性矩为2200 kg·m2，构架垂向惯性矩为2200 kg·m2，车体纵向惯性矩为0.6×106kg·m2，车体垂向惯性矩为0.6×106kg·m2，轮轨黏着因数为0.6×106。

文献[25]描述了一种在固定坐标系(笛卡尔坐标系)中建立车辆-轨道系统模型的方法，通过在模型中输入常用制动和紧急制动工况时的制动转矩mf，得出制动工况下的速度曲线。通过这种方法建立轮对与轨道之间的接触，轮轨接触约束方程为：

C(q，s，t)=0，

(1)

式中：q、s分别表示接触体的广义坐标和非广义表面参数向量，t为时间。

将式(1)对时间进行2次微分得

(2)

简化式(2)得:

(3)

式中：Qd为广义坐标和表面参数的二阶导数矩阵，Cq为q的次雅可比约束矩阵，Cs为s的次雅可比约束矩阵。

对轮轨-轨道多体动力学模型进行受力分析，结合式(1)～(3)可得出含接触约束的动力学平衡方程

(4)

式中：m为质量矩阵；Q为施加到轮对的外力，包括重力、蠕滑力、悬挂力和制动力矩阵；Qd为二次速度矢量；λ为拉格朗日因子，可用于确定法向接触力。

采用Matlab求解式(4)，计算流程图如图2所示，从而得到车辆-轨道动力学响应。

图2 动力学方程求解流程

求解动力学方程时，轨顶初始坐标为(0，0，0)，则车轮的初始坐标为(0，0，R/2)(R为车轮半径)。在检测车轮接触点时，采用实测的车轮和轨道外形作为初始数据，同时输入车轮的周期性不圆缺陷值，通过设定初速度和计算时间，输入制动转矩，求解制动状态下的动力学平衡方程式，随着列车制动力的施加，直至列车速度为零时程序终止。

1.2 不圆缺陷描述

将整个车轮圆周上的谐波缺陷作为周期性车轮不圆(假设不圆缺陷沿着车轮外形轮廓近似均匀分布，形成多边形车轮外形)，车轮不圆缺陷可描述为：

Z=Asin[iψ+φi],

(5)

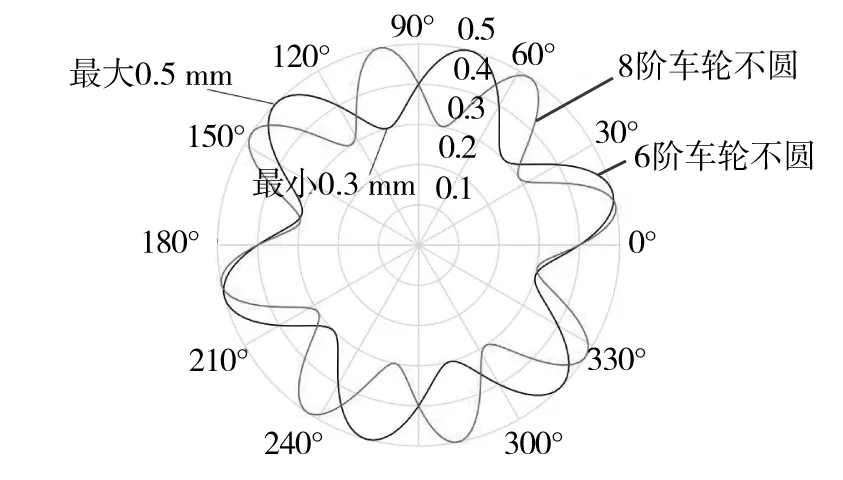
图3 6阶与8阶车轮不圆缺陷示意图

式中：Z为车轮垂向位移；i为缺陷的计数器，称为阶数；A为车轮不圆缺陷的幅值，定义为正弦曲线的最大值和最小值之差的一半；φi为相位滞后；ψ为极坐标，ψ=vt/R，其中，v为车辆运行速度，R=0.425 m。 6阶与8阶车轮不圆缺陷用极坐标表示，如图3所示。

图4 试验与仿真轮对制动减速度对比

1.3 模型验证

为了进一步验证动力学模型的合理性，将模型计算结果与动力学试验数据进行对比，在转向架上施加持续6 s的常用制动转矩，在轮对上采集加速度数据。图4显示了通过仿真和试验获得的轮对制动减速度。从图4可以看出：仿真结果与试验数据吻合良好，最大误差仅为6%，验证了所建动力学模型的准确性。

2 动力学仿真与结果讨论

根据车轮不圆缺陷的几何形状和动力学模型，在Matlab中对车辆在常用和紧急制动工况下的动态响应进行仿真计算。

列车以80 km / h的初始速度匀速行驶，常用制动工况是在列车运行1 s后施加制动转矩，制动转矩在4 s内从0缓慢增加到8 kN·m；紧急制动工况则在列车运行1 s后立即施加8 kN·m的制动转矩，并保持不变，直到轮对停止。仿真中，假设所有车轮均有车轮不圆缺陷，讨论车辆前转向架和前轮对的动力学响应结果。根据已知列车数据计算列车出现滑行的临界制动转矩为11 kN·m，因此，本文中施加8 kN·m的最大制动转矩，不会出现车轮抱死滑行现象[26]。

制动转矩施加的时间历程如图5所示，制动过程中车轮的速度和角速度变化如图6所示。从图6中可以看出：车辆的速度和角速度随着制动转矩的施加而逐渐减小，在常用制动和紧急制动过程中均无滑行现象出现。

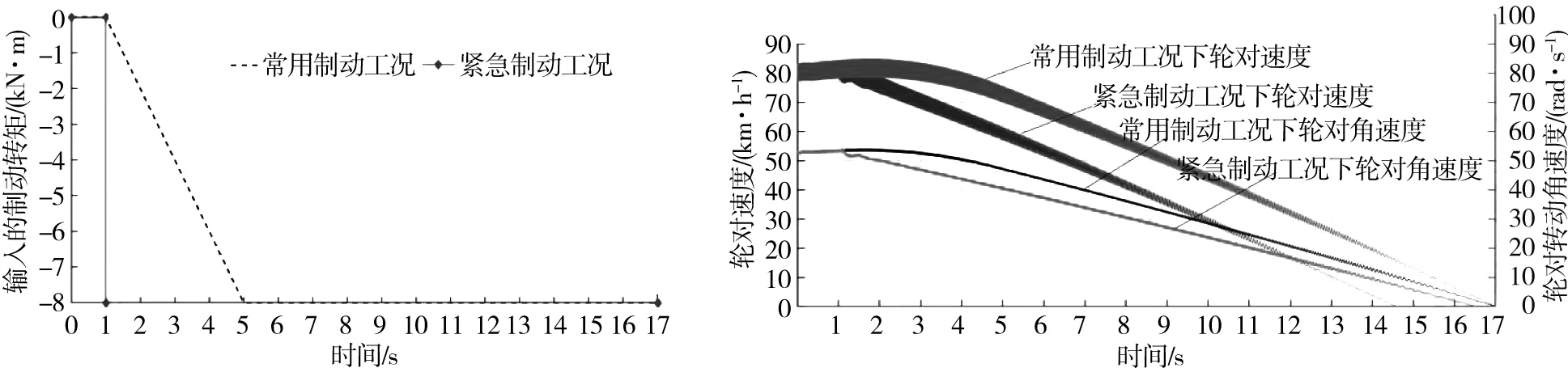
图5 制动转矩施加时间历程图 图6 车辆速度和角速度变化曲线

2.1 制动工况下的垂向动力学响应

图7、8给出了轮对在周期性车轮不圆和无缺陷车轮激励下的垂向响应。由图7、8可以看出，在常用制动工况下，车辆先匀速运行1 s，然后运行16 s停止；在紧急制动工况下，车辆运行13.5 s停止。2种工况下，车辆的速度和轮对的转动角速度同时为0，没有产生滑行。轮对的垂向加速度随着车轮的不圆变化而振荡，随着制动转矩的施加，紧急制动较常用制动工况的振荡频率和振动幅度减小。

构架和车体在常用和紧急制动工况下的垂向加速度响应的时间历程如图9～12所示。

图9 常用制动时构架的垂向加速度响应 图10 紧急制动时构架的垂向加速度响应

图11 常用制动时车体的垂向加速度响应 图12 紧急制动时车体的垂向加速度响应

由图9～12可知：构架和车体的振动频率和峰值逐渐减小，最终保持稳定；与轮对的振动幅值相比，构架和车体的振幅都较小，说明车轮不圆对构架和车体的垂向响应的影响较小。值得注意的是，在车辆运行速度约为30 km/h时，轮对的固有纵向振动频率为13.45 Hz，该频率刺激了轮对的纵向振动，使构架和车体的垂向加速度出现了小幅的增加。

从图9、10可以看出，紧急制动时构架的垂向响应总体趋势与常用制动情况相似。由图11、12可以看出：车轮不圆引起的轮轨力属于一种高频力，在制动状态下，受二系悬挂的影响，车体对车轮不圆的垂向振动响应更为明显。

2.2 制动工况下的纵向动力学响应

车辆制动过程中，在车轮不圆激励和制动转矩的作用下，常用制动和紧急制动工况下轮对、构架和车体的纵向动力学响应如图13～18所示。由图13～16可知：车轮不圆对轮对和转向架构架纵向加速度的影响比无缺陷车轮明显，纵向振动加速度幅值随着车辆速度的减小而降低。由图17、18可以看出：在车轮不圆的激励下，由于一系和二系悬挂阻尼的衰减作用，车体的纵向最大加速度(绝对值)为3 m/s2;在车辆启动后1 s内，装有无缺陷车轮的车体纵向加速度为0，由于启动时车轮不圆产生的纵向蠕滑力的影响，有不圆缺陷车轮的车体加速度先增加后逐渐趋于稳态。

由图13、14可知：在车辆运行速度为30 km/h时，即车辆大约运行11 s时，车轮不圆导致的纵向振动频率和轮对的自然纵向振动频率接近，产生了共振效应。

图13 常用制动时轮对的纵向加速度响应 图14 紧急制动时轮对的纵向加速度响应

图15 常用制动时构架的纵向加速度响应 图16 紧急制动时构架的纵向加速度响应

图17 常用制动时车体的纵向加速度响应 图18 紧急制动时车体的纵向加速度响应

3 结论

在建立的车辆动力学模型的基础上，采用实测的车轮和轨道外形数据分析了周期性车轮不圆常用和紧急制动情况下的车辆垂向和纵向响应。

1)车轮的不圆缺陷大大增加了垂向和纵向加速度，而且纵向加速度始终大于垂向加速度；

2)由于悬挂装置的衰减特性，所有方向的加速度从轮对到车体都迅速衰减；

3)对于无缺陷车轮和有不圆缺陷的车轮，车体加速度变化趋势比较相似，所以需要高灵敏度的传感器和算法才能从车体上测出车轮的不圆缺陷；将加速度传感器安装在车轮或构架上能更好的检测到车轮的不圆缺陷。

4)制动力对垂向和纵向加速度的影响比车轮不圆缺陷产生的影响要小，与无缺陷车轮相比，有不圆缺陷车轮的制动力对加速度的影响更明显。