双向变速绿波控制在有轨电车共线场景下的应用
2020-12-03杨海飞
翟 学,吴 中,杨海飞
(河海大学 土木与交通学院,江苏 南京 210098)
现代有轨电车[1]作为一种使用清洁能源的公共交通工具,具有安全、容量较高和环境协调的优点,当前正在我国城市快速发展。由于有轨电车在地面轨道上运行,其线路常常与城市道路发生共线或交叉,这使城市干道的交通管理和控制更加复杂。有轨电车与普通城市道路共线给信号协调控制[2]也提出了新的要求。
国内外学者对信号协调控制的研究主要集中在两个方面:最小延误优化[3]和最大绿波带宽优化[4]。其中最小延误优化模型的求解过程较为复杂,而最大绿波带宽则得到了更为广泛和深入的研究。1966年,LITTLE等提出混合整数线性规划模型[5];并和KELSON等使用最大绿波相位差优化方法开发了MAXBAND最大绿波带优化程序[6];而后CHANG[7]、GARTNER[8]等人对该模型进行了改进,分别提出可适应多干路的路网协调控制模型MAXBAND-86和适应不同路段的交通流量、不同的通行条件的可变带宽的MULTIBAND模型[9]。国内马楠等[10]给出基于双向绿波带宽最大化的优化模型;卢凯等[11]考虑了带宽的分配影响因子和需求比例系数建立了双向不同带宽需求的协调优化模型;朱和等[12]提出一种基于灵活相位相序的改进MAXBAND模型;曲大义等[13]运用交通波理论阐释了大流量条件下线控系统的车辆排队现象,并以下游交叉口无排队车辆为目标,建立了基于交通波理论的交叉口相位差优化模型。
上述模型大多固定了通行带的速度,但受条件限制,双向带宽往往较窄,在有轨电车与社会车辆共线的场景下较难发挥应有的作用。吴中、舒毅、李垣君、张静伟等[14-16]首次提出在交叉口间距和道路速度限制约束下,绿波带路段速度可变的双向变速绿波方案,进而提出变速点在路段中间的恒速通过交叉口方案,解决了因变速带来的交通波影响的问题。既有的研究表明双向变速绿波模型下的车辆变速可以较好地适应双向交通量均较大的工况,也在很大程度上解决了双向绿波带宽不足的难题。
本文的研究结合城市地面有轨电车与社会车辆共线的发展趋势,将变速绿波模型应用到包含有轨电车的城市干道中,在保证有轨电车正常通过的同时,也确保实现道路的双向绿波功能,进一步拓展了双向绿波的应用,也验证双向变速绿波控制在城市干道有轨电车运行环境下的有效性。
1 双向变速绿波基本模型
双向变速绿波的控制方案主要解决干道交叉口间距不一、横向交叉口密度大、双向车流难以在同一时间到达同一交叉口的问题,通过让双向交通流按照预定的方案在时空上进行变速,以获得更大的绿波带宽。基本模型表达式如下[15]:
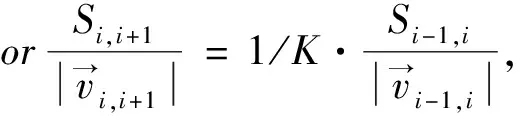
i+1≤m;i-1≥1。
(1)
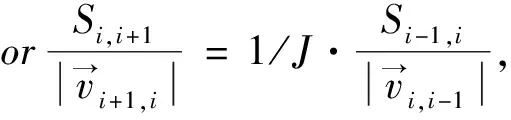
i+1≤m;i-1≥1。
(2)
(3)
(4)
(5)
(6)
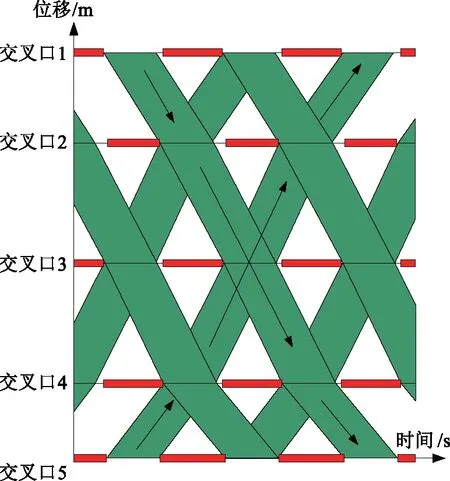
图1 双向变速绿波时距示意图
双向变速绿波控制使车辆能够最大化地利用绿灯时间,改变了以往固定带速在城市干道交叉口间距不一条件下带宽过窄的局限性和可行带宽搜索的困难性,在绿波设计的应用上提供了更多的灵活性。
2 应用场景
道路位于加利福尼亚州萨克拉门托市中心的一条有轨电车线路,有轨电车线路和社会车辆共线,且会在客流集中的地点设置停靠车站。道路交叉口间距不一,有轨电车在某一交叉口处转向,电车轨道采用单轨双向中央布设,设定车站均位于路段中间,见图2。
推荐理由:所有孩子,都渴望被看见……一个并不“存在”的孩子,该如何去寻找真实的自我?这是一部让你看过之后眼里噙着泪水,嘴角却漾起微笑的暖心幽默小说;一部能帮助孩子不再成为“隐形人”的创意文学佳作;一本能启发孩子无限想象力的写作指导手册……
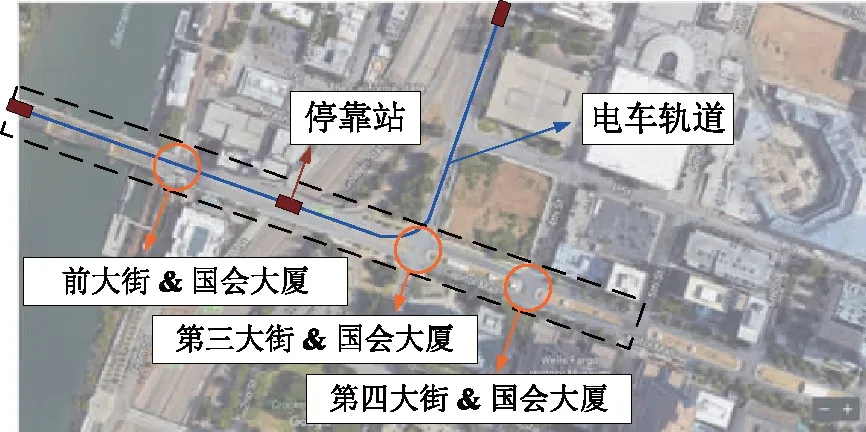
图2 有轨电车与道路共线场景图
在有轨电车实际运行过程中,由于经济效益的考量以及提供更加便利、舒适的乘车体验,通常会对电车进行优先控制,这往往会导致电车和社会车辆在交叉口的通行权冲突,具体表现在信号相位差或相序的改变,对原有的传统方式干线绿波控制造成干扰甚至使其难以实施,增加了干道上运行的社会车辆的延误,降低了干道的通行能力。
以往传统的绿波控制对交叉口信号相位的改变适应性较弱,而双向变速绿波控制在绿波设计上的灵活性则提供了一种解决问题的可能。
考虑电车的运行稳定性,设定电车的运行速度和在停靠站停车上下客的停留时间基本固定,具体应用步骤分为以下几步:
Step1:选定合适的电车运行速度和电车停靠站点;
Step2:作出电车双向时空运行轨迹;
Step3:根据文献[15],在时空图中作出社会车辆双向绿波带;
Step4:校核绿波方案能否协调电车运行轨迹,使得电车不停车地通过交叉口。若不满足,则重新调整电车运行速度和发车时刻,返回Step2,反之结束。
图3展示了双向变速绿波在有轨电车共线场景下应用的设计时距图。在有轨电车预定轨迹下,通过社会车辆的双向变速行驶,使得上下行的有轨电车和社会车辆均实现绿波通行,最大化社会车辆的运行效益。
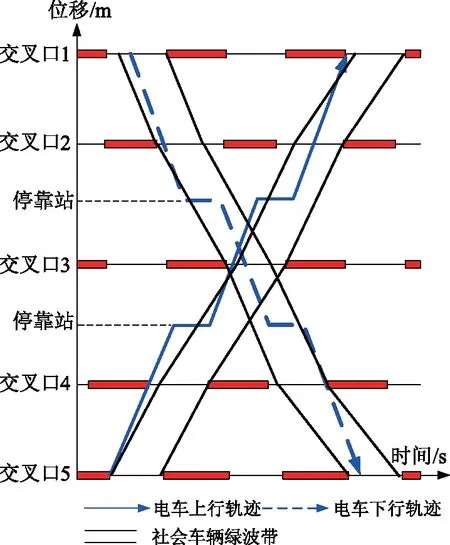
图3 有轨电车场景下双向变速绿波时距图
3 仿真评价
3.1 道路概况
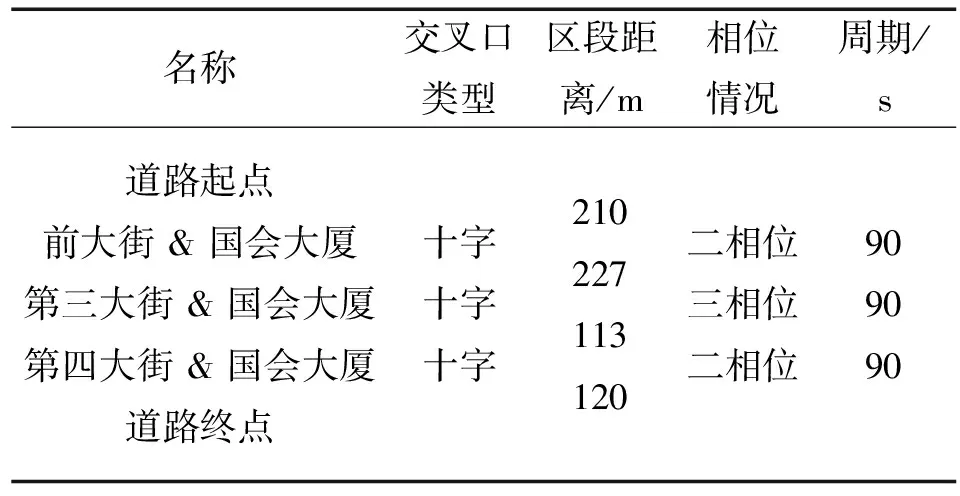
表1 场景道路基本信息
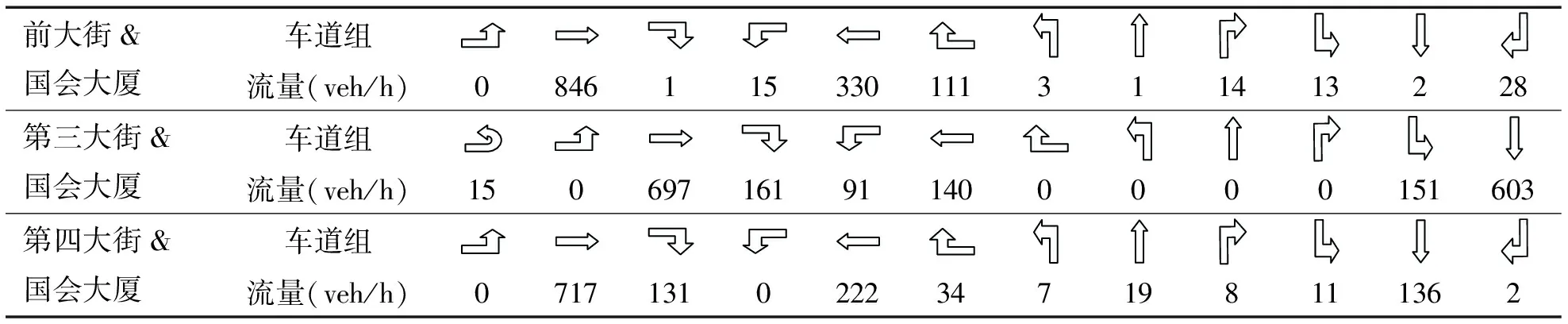
表2 各交叉口早高峰流量
3.2 仿真方案
对社会车辆分别采用传统双向绿波控制[17](方案1)和双向变速绿波控制方案(方案2),各方案下电车发车时刻和信号配时参数如下表所示。表3为方案1的电车发车时刻及干线信号配时参数;表4为方案2下的电车发车时刻及干线信号配时参数。两种方案下有轨电车发车时刻、发车间隔、主路绿信比和周期均保持一致,因此在保证有轨电车通行效率不变的前提下,可以认为两种方案对支路的影响近似相等。

表3 方案1电车发车时刻及信号配时参数

表4 方案2电车发车时刻及信号配时参数
3.3 结果与评价
利用AnyLogic仿真软件及多智能体建模技术,仿真得到各方案下连续运行两小时的数据,取其中一小时(1 800 s至5 400 s)作为仿真结果。选取主路社会车辆的速度-位置分布、行程时间、停车次数以及流量作为评价指标。
3.3.1速度-位置分布
由图4和图5可以发现,上行车辆在交叉口R1(前大街 & 国会大厦)和R2(第三大街 & 国会大厦)的上游路段中速度发生周期性的上升和下降。其中方案1的上行车辆在交叉口R3(第四大街 & 国会大厦)前会产生速度的下跌乃至拥堵;方案2的上行车辆则基本能够不停车地通过交叉口R3,缓解了交叉口R3前的拥堵。两种方案的上行车辆均会在交叉口R1和R2前产生拥堵和排队,这是由于高峰小时主路上行方向交通量过大导致的。
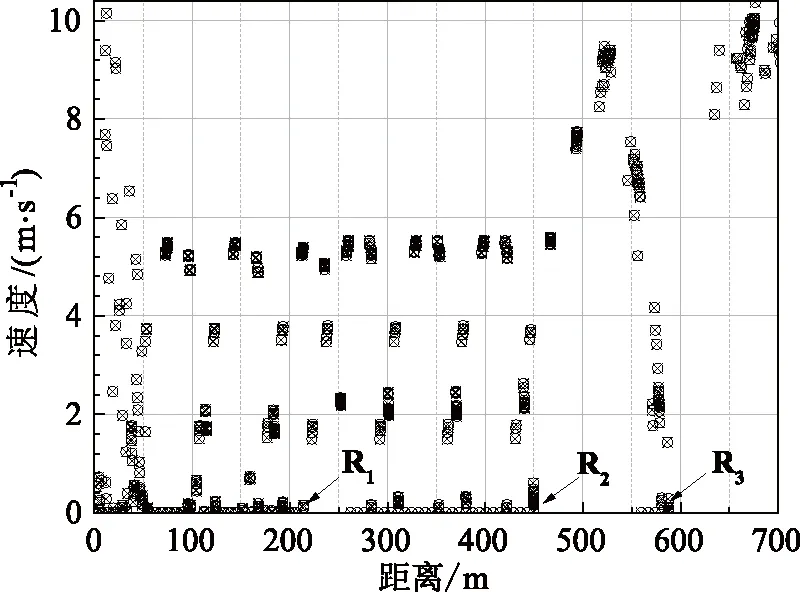
图4 方案1速度-位置分布上行方向
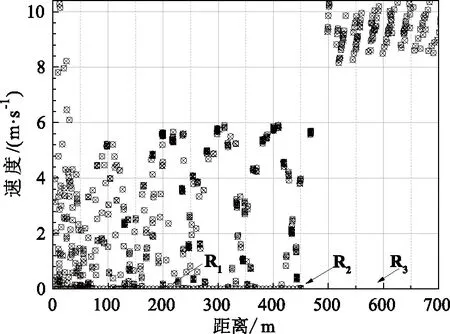
图5 方案2速度-位置分布上行方向
图6和图7展示了两种方案下的下行车辆的速度-位置分布图。可以发现,方案2较方案1缩短了交叉口R2前车辆的排队长度,并使车辆能够通过变速不停车地通过交叉口R1,优化效果较为明显。

图6 方案1速度-位置分布下行方向

图7 方案2速度-位置分布下行方向
3.3.2行程时间
通过记录每辆车出入路段的时间,得到每辆车的行程时间,图8和图9展示了不同方案下主路上下行社会车辆的行程时间随时间变化的曲线图。可以看出,在仿真时段内,方案1和方案2的上下行车辆平均行程时间均随时间在某一区间内变化,且方案2的曲线总体位于方案1的曲线下方。
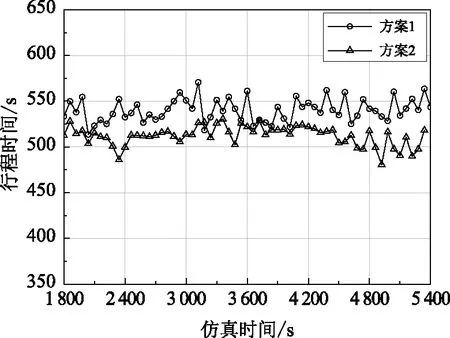
图8 行程时间变化曲线上行方向
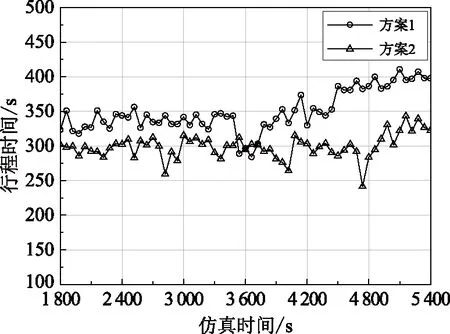
图9 行程时间变化曲线下行方向
不同方案的行程时间数据的单因素方差分析结果如表5所示,结果表明数据均在0.05水平上显著性差异。对于上行车辆的平均行程时间,方案2较方案1下降5.3%;对于下行车辆平均行程时间,方案2较方案1下降13.6%。总体上与方案1相比,方案2车辆行程时间的最大值和最小值均较低,且标准差较小,数据分布更加集中,这是由于在方案2中更多的车辆能够同步行进,从而行程时间较为接近。

表5 行程时间的单因素方差分析汇总统计
3.3.3停车次数
不同方案下社会车辆停车次数的单因素方差分析结果如表6所示,结果表明数据均在0.05水平上显著性差异。从平均停车次数来看,对于上行车辆,方案2较方案1下降14.8%;对于下行车辆,方案2较方案1下降14.0%。可以发现,同方案1相比,方案2的上下行社会车辆停车次数最大值和最小值均稍有减小或者持平,对于行车更加拥堵的上行方向这种优化更加明显,这是由于方案2中有更多的车辆能够通过变速不停车地通过交叉口。

表6 停车次数的单因素方差分析汇总统计
3.3.4流量
不同方案主路流量的单因素方差分析结果如表7所示,结果表明数据均在0.05水平上显著性差异。对于上行方向平均流量,方案2较方案1提高12.5%;对于下行方向平均流量,方案2较方案1提高13.3%。总体来看,方案2在上下行方向均提高了主路流量的最大值和最小值,但标准差略有提高。一方面,方案2中一个周期内有更多的的车辆能够通过交叉口,另一方面,周期性的控制也可能导致部分时段流量的差异。
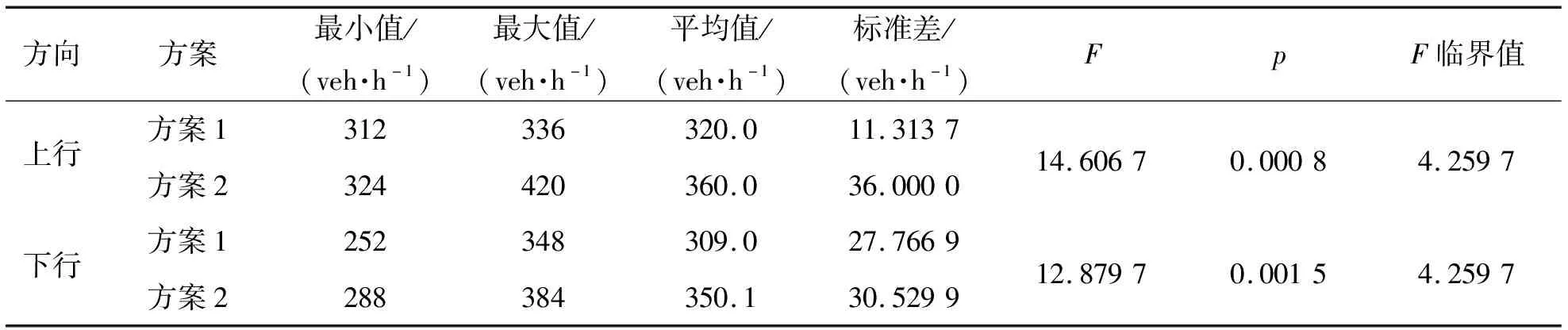
表7 流量的单因素方差分析汇总统计
4 结论
通过在以上场景的实际应用,可以发现只要合理地选定电车的运行速度、停靠站点以及发车时刻,就能够采用双向变速绿波设计方案在有轨电车和社会车辆的共线场景下进行较好地应用。通过引导社会车辆在交叉口前变速,缓解了交叉口前的拥堵、降低了主路社会车辆的平均行程时间和停车次数,并提高了主路的通行能力。相比于传统的双向绿波模型,双向变速绿波控制能够兼顾电车和社会车辆的运行效率,更好地适应城市干道有轨电车运行的场景。
此外,由于本文对社会车辆变速点的选择位于交叉口,如果将变速点移至路段当中,则双向绿波的效果可能会有进一步的提高。
