不同加载方式下页岩强度与变形的尺度效应规律试验研究

2020-12-03陈军斌赵庆磊

石油钻探技术 2020年5期

李帅，陈军斌，赵庆磊

（1.西安石油大学石油工程学院，陕西西安 710065；2.中国石油集团川庆钻探工程有限公司长庆井下技术作业公司，陕西西安

710016）

页岩储层孔隙度和渗透率极低，必须依靠水平井与体积压裂的协同作业才能获得高效开发。从岩石力学角度来讲，水平井与体积压裂协同作业成功实施的关键是能准确把握储层岩石的强度与变形特征。目前，室内小尺度岩样力学试验仍然是获取页岩强度与变形特征的主要方法，但页岩层理结构发育，局部微裂隙广泛分布，非均质性极强。研究表明，岩石非均质性越强，其强度与变形的尺度效应现象就越显著[1]。因此，深入研究页岩强度与变形的尺度效应规律，具有现实意义。同时，大量研究发现，加载方式也是影响岩石强度与变形尺度效应规律的重要因素。例如，张明等人[2]研究发现，三点弯曲试验的岩石强度的尺度效应最明显，单轴拉压试验次之，存在侧压的压缩试验最不明显；唐伟等人[3]研究发现，岩石围压越大，其强度与变形的尺度效应就越弱；徐燕飞等人[4]研究发现，岩石的单轴抗压强度越大，其抗拉强度的尺度效应越明显；邓树新等人[5]研究发现，围压越大，岩石强度尺度效应越不明显。由此可见，加载方式显著影响着岩石强度与变形的尺度效应。为此，笔者制作了46 块不同尺度的页岩岩样，分别进行了三轴压缩、单轴压缩和巴西劈裂试验，分析了不同加载方式下页岩强度与变形的尺度效应，初步得到了不同加载方式对页岩强度与变形尺度效应产生影响的机理。

1 试验设计

1.1 试验岩样

试验岩样取自鄂尔多斯盆地长7 段页岩露头。该页岩露头所在地区构造平缓，地层连续，露头保存良好。考虑页岩的力学性质各向异性明显，试验岩样均沿平行层理方向钻取，表面无裂隙；同时，为使试验结果具有代表性，调研了前人研究岩石强度与变形尺度效应及相关问题时选择的岩样尺度跨级和范围，发现岩样尺度跨级多为3～6 级，尺度集中在100.00 mm 以内[6-9]。因此，笔者将三轴压缩试验的岩样制作成直径25.00 mm、高度10.00～70.00 mm、尺度跨级为12 级的岩样组，单轴压缩试验的岩样制作成高径比为2.0、直径17.06～38.22 mm、尺度跨级为4 级的岩样组，巴西劈裂试验的岩样制作成直径50.00 mm、高度15.26～30.17 mm、尺度跨级为4 级的岩样组；为保证试验数据准确，每个尺度至少制备2 块岩样。

1.2 试验仪器

页岩单/三轴压缩试验采用美国的RTR-1000 型岩石三轴力学伺服测试系统，仪器最大轴向压力为1000 kN，最大围压和孔隙压力均为140 MPa，最高温度为150 ℃，压力、流体体积和变形的精度分别为0.01 MPa、0.01 mL 和0.001 mm。巴西劈裂试验采用600 kN 伺服试验机，仪器最大围压为90 MPa，最高温度为100 ℃，压力和变形的精度分别为0.1 MPa和0.001 mm。

1.3 数据处理

目前，基于经典岩石强度与变形尺度效应理论（Weibull 脆性破坏理论、Griffith 微裂纹强度理论和应变局部化理论等）建立的岩石强度、变形参数与尺度的关系模型均为幂函数摸型。因此，在特定区间内，页岩各强度、变形参数与尺度也呈良好的幂函数关系，而非无序变化。基于该认识，对页岩三轴压缩、单轴压缩和巴西劈裂试验的各强度、变形参数与尺度均进行幂函数拟合，并认为由于影响页岩强度与变形的因素多而复杂，当各参数幂函数拟合的决定系数R2大于0.5 时，即可认为该参数具有明显的尺度效应[10-11]，对于具有明显尺度效应但无法进行幂函数拟合的参数采用对数拟合，对于没有明显尺度效应的参数（决定系数R2小于0.5）采用线性拟合。任意尺度下页岩各力学参数的代表值等于该尺度下各测试岩样对应参数测试结果的算术平均值。

2 页岩三轴压缩试验

2.1 强度与变形参数

为了了解端部摩擦效应和非均质性对页岩强度与变形尺度效应的影响，用24 个岩样（记为A1，A2，…，A24）进行了三轴压缩试验（围压20 MPa）。试验时，将12 个跨级的岩样分为2 类：一类为高径比范围（0.4～2.0]，共7 级；另一类为高径比范围（2.0～2.8），共5 级。试验结果如图1 所示。

由图1（a）可知，岩样高径比不小于2.0 和小于2.0 时，弹性模量与高径比均呈良好的幂函数关系，且岩样弹性模量随岩样尺度增大而增大，但增大幅度逐渐减小。

由图1（b）可知，高径比小于2.0 时，其与岩样泊松比具有良好的幂函数关系；但高径比大于2.0 后，泊松比与岩样高径比更趋于呈线性关系。泊松比表征了页岩的横向变形能力，岩样高径比小于2.0 时，页岩横向变形能力随岩样尺度增大而增大；而高径比大于2.0 时，其横向变形能力基本不变。

图1（c）为峰值强度与高径比的关系。岩样高径比小于2.0 时，峰值强度基本不随岩样尺度变化而改变；但当高径比大于2.0 时，峰值强度与高径比呈对数关系。峰值强度表征的是页岩产生宏观破坏时所能抵抗外力破坏的能力，可以看出，高径比小于2.0 时，页岩抵抗外力破坏的能力基本不变；而高径比大于2.0 时，页岩抵抗外力破坏的能力逐渐增强，并趋于稳定。-般而言,岩石强度随岩样尺度增大而减小;但高径比大于2.0时,页岩强度逐渐增大,说明三轴压缩时高径比大于2.0的页岩上一尺度的缺陷层次(缺陷尺寸与试件尺寸之比)比下一尺度高,而缺陷层次越高，岩石强度越低[7]。

图1 三轴压缩试验得到的岩样强度、变形参数与尺度的关系Fig.1 Relationship between scale and strength and deformation parameters of rock samples obtained from triaxial compression test

由图1(d)可知,岩样高径比小于2.0时,峰值应变随高径比增大而减小,决定系数为0.51;高径比大于2.0时，峰值应变与高径比无明显关系。峰值应变能较为准确地表征页岩的脆性,峰值应变越小，页岩的脆性越强。因此，页岩高径比小于2.0时，其脆性随岩样尺度增大而增大。

由图1(e)可知，岩样高径比大于2.0或小于2.0时,残余应力与高径比之间离散性较强，无明显规律。图1(f)为残余应变与高径比的关系，分析可知，高径比小于2.0时，残余应变离散性很强，但趋于在平均值2.31附近波动;高径比大于2.0时,残余应变与高径比呈幂函数关系。残余应变可以表征页岩在产生宏观破坏后抵抗外力进--步破坏的能力，残余应变越大，页岩抵抗外力进一步破坏的能力越强。从残余应变角度而言，高径比小于2.0 时，页岩破坏后抵抗外力进一步破坏的能力基本不变；高径比大于2.0 时，页岩破坏后抵抗外力进一步破坏的能力逐渐降低。

图1（g）为破裂时间与高径比的关系曲线。分析可知，高径比小于2.0 时，岩样破裂时间与高径比的幂相关性相对较差；但高径比大于2.0 时，破裂时间随高径比增大而缩短，并呈幂函数关系。破裂时间是岩样从开始加载到产生宏观破裂的时间，破裂时间越短，说明岩样脆性越高。因此，从破裂时间角度而言，高径比大于2.0 时，岩样脆性随高径比增大而增强。

由图1（h）可知，岩样高径比大于2.0 和小于2.0 时，破裂面数量与高径比之间的相关性均较差；但是，高径比大于2.0 时，破裂面数量随高径比的增大而逐渐趋于稳定，均值为1.5 个。破裂面数量指岩样破坏后所形成的宏观破裂面的数量，破裂面越多，页岩破碎越充分，越有利于油气渗流。破裂面数量与尺度的关系说明页岩始终存在优势破裂面，即在单一外力作用下难以形成复杂的裂缝网络。因此，实际的页岩储层必须依赖体积压裂技术形成复杂裂缝网络，才能获得有效产能。

综上所述，页岩高径比大于2.0 和小于2.0 时，各强度、变形参数随尺度变化的规律往往不同，部分参数在2 个区间内的数值和变化规律差异巨大，且在高径比为2.0 的过渡尺度处出现骤降或骤升现象，这都说明端部摩擦作用会对页岩强度与变形产生巨大影响。当前，我国页岩油气开发刚刚起步，井下岩样异常珍贵，研究人员参考国际岩石力学学会规定三轴压缩试验时岩石高径比大于2.0 是相对安全值，有时采用高径比略小于2.0 的岩样来测试页岩力学参数，上述试验结果表明，这样的处理是极不严谨的。因此，页岩三轴压缩试验时，选择岩样的尺度非常重要，一方面必须严格规避端部摩擦效应的影响，另一方面也要充分考虑岩样非均质性对强度与变形参数尺度效应的影响。

2.2 应力应变曲线

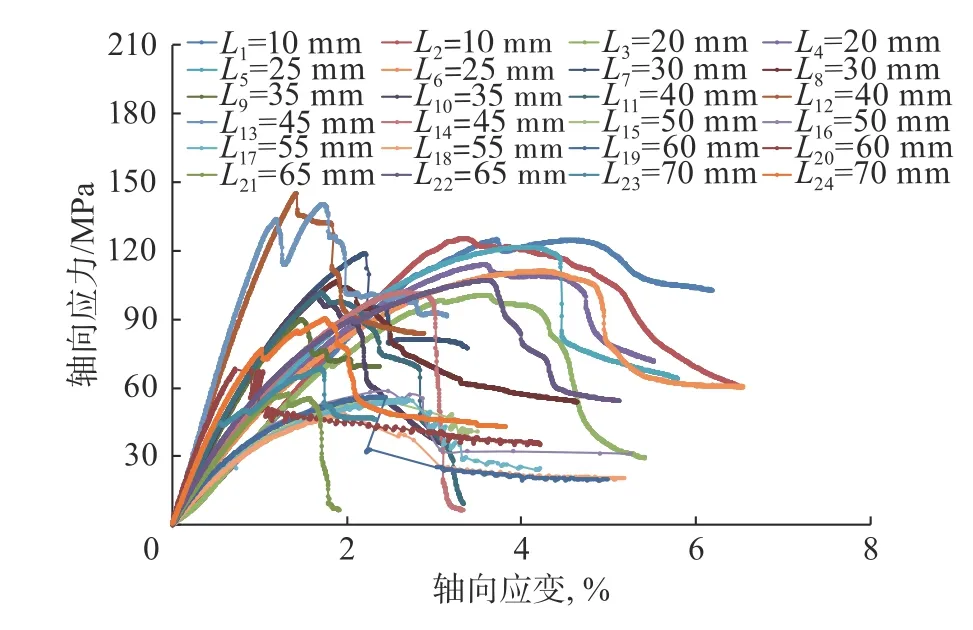
图2 三轴压缩试验得到的应力应变曲线Fig.2 Stress-strain curve obtained from triaxial compression test

根据岩样是否破坏，将应力应变曲线分为峰前段和峰后段（见图2；其中，L1，L2，…，L24分别为岩样A1，A2，…，A24 的长度，mm）。从图2 可以看出，三轴压缩试验得到的不同尺度页岩岩样的应力应变曲线，除极个别岩样存在压密段外，大多数岩样的峰前段均可分为线性变形段和塑性屈服段，且岩样产生宏观破坏后承受外力的能力并未直接降为0，而是逐渐进入应力残余段，即不同尺度页岩岩样的应力应变曲线均经历了线性变形段、塑性屈服段、峰后破坏段和应力残余段等4 个阶段（见图3）。换言之，从变形分段角度看，页岩三轴加载时应力应变曲线并不存在尺度效应。页岩典型的应力应变曲线特征与各强度和变形参数的尺度效应相结合，可有效预测包括页岩岩体在内的其他尺度页岩的强度与变形特征。

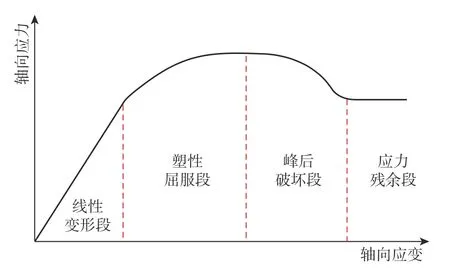
图3 三轴压缩试验得到的应力应变曲线的特征Fig.3 Characteristics of stress-strain curves obtained from triaxial compression test

2.3 破坏形态

进行三轴加载后，不同尺度页岩的破坏形态如图4 所示。由图4 可知，高径比为0.4 的岩样A1 和A2 其破坏形态为拉伸破坏，而高径比为0.8～2.8 的岩样为剪切破坏，即对于高径比大于2.0 的岩样，其破坏形态不存在尺度效应。

图4 三轴压缩试验中的岩样破坏形态Fig.4 Failure forms of rock samples in triaxial compression test

不同尺度岩样的破坏形态不同，反映了其受力状态的不同。对于高径比小于2.0 的岩样，其破坏形态受自身非均质性和端部摩擦作用共同控制，岩样尺度越小，端部摩擦作用越强。目前，尚无法从理论及数学模型角度推导出岩石破坏过程中端部摩擦力的数值及变化规律，也无法定量刻画岩石非均质度与其强度、变形的关系。因此，目前很难从数值角度确定岩石端部摩擦效应和非均质性对岩石强度与变形起主导作用的临界尺度，但页岩作为一种层理结构发育的岩石，可根据破坏形态间接确定该临界尺度。因为在三轴压缩试验中，页岩破坏形态主要受层理弱结构面和微缺陷弱结构面控制，对于尺度较小的岩样，其所受端部摩擦力可等效为给岩样额外加载了限制其横向变形的“围压”，且离端部越近，该“围压”作用越强，此时岩样在加载的侧压及摩擦作用导致的“围压”双重作用下，内部微裂纹、微裂隙等缺陷紧紧闭合，使岩样非均质性显著降低，导致页岩破坏的不稳定面只有层理弱结构面。因此，页岩此时主要发生沿层理方向的破坏，即拉伸破坏，如岩样A1 和A2。换言之，此时端部摩擦作用是影响页岩强度与变形尺度效应的主导因素。但随着岩样尺度增大，端部摩擦所造成的“围压”大小及作用范围相对于岩样强度和尺度越来越小，而页岩内部出现较大尺度缺陷的概率和数量相应增大，即非均质性明显增强，此时页岩破坏主要由微缺陷所形成的弱结构面控制。由于微缺陷的分布是不规则和不均匀的，页岩会产生沿不同角度的剪切破坏，即高径比不小于0.8 后，非均质性成为影响页岩强度与变形尺度效应的主导因素。

因此，页岩端部摩擦效应和非均质性对其强度与变形尺度效应起主导作用的临界高径比为0.4～0.8；当高径比不小于0.8 时，非均质性是主导因素，但这也并不意味着端部摩擦作用完全消失。端部摩擦效应和非均质性对岩石强度与变形尺度效应的影响是非常复杂的，目前仍无法完全掌握影响规律，本文仅通过页岩破裂形态尝试性地得到了二者的临界值，其精度和准度可能仍需进一步提高。

3 页岩单轴压缩试验

3.1 强度与变形参数

用11 个岩样（记为B1，B2，…，B11）进行了页岩单轴压缩试验，得到的岩样强度、变形参数与尺度的关系如图5 所示[12]。由图5 可知，除破裂面数量外，页岩单轴压缩时各强度与变形参数均具有明显的尺度效应，其中弹性模量、泊松比随岩样尺度增大而增大，峰值强度、峰值应变、残余应力、残余应变和破裂时间随岩样尺度增大而减小。

3.2 应力应变曲线

单轴压缩试验得到的应力应变曲线分段变形特征如图6 所示[12]，可以看出，应力应变曲线不存在尺度效应现象，岩样从开始加载到破坏均要经历压密段、线性段、脆性破坏段和应力残余段等4 个阶段。

3.3 破坏形态

单轴压缩试验的页岩岩样破坏形态如图7 所示[12]，可以看出，破坏形态不存在尺度效应，均为剪切角小于10°的拉伸-剪切复合破坏。

由图7 可知，单轴压缩时，页岩破坏以层理弱结构面破坏为主，这与三轴压缩中高径比不小于0.8的岩样以贯穿层理面的微缺陷弱结构面破坏存在明显差异，且部分岩样中部出现“膨胀”现象，说明单轴压缩试验中即便岩样高径比为2.0，其强度与变形在一定程度上仍受到端部摩擦效应的影响，但三轴压缩时岩样中部未见“膨胀”，说明围压会在一定程度上遏制端部摩擦对岩石强度与变形的影响。

4 页岩巴西劈裂试验

4.1 强度与变形参数

巴西劈裂试验是测试页岩抗拉强度的一种简单而快捷的方法。为此，用11 个岩样（记为C1，C2，…，C11）进行了巴西劈裂试验，得到的岩样各强度、变形参数与尺度的关系如图8 所示[13]。

图5 单轴压缩试验得到的岩样强度、变形参数与尺度的关系Fig.5 Relationship between scale and strength and deformation parameters of rock samples obtained from uniaxial compression test

图6 单轴压缩试验得到的应力应变曲线的特征Fig.6 Characteristics of stress-strain curve obtained from uniaxial compression test

图7 单轴压缩试验得到的岩样破坏形态Fig.7 Failure forms of rock samples obtained from uniaxial compression test

图8 巴西劈裂试验得到的岩样强度、变形参数与尺度的关系Fig.8 Relationship between scale and strength and deformation parameters of rock samples obtained from Brazilian splitting test

由图8 可知，巴西劈裂试验得到的页岩最大载荷、抗拉强度、峰值强度和破裂面数量均具有明显的尺度效应，其中最大载荷、峰值强度和破裂面数量随岩样尺度增大而增大，抗拉强度随岩样尺度增大而减小，峰值应变、残余应力、残余应变和破裂时间不存在明显的尺度效应。残余应力、残余应变与尺度之间没有规律性关系，主要是由其离散性导致的，如岩样C1、C7、C8 和C11 等不存在应力残余段，但其他尺度的岩心却存在应力残余段。峰值应变和破裂时间随着岩样尺度增大而趋向于在一个平均值附近波动，说明在巴西劈裂试验中，页岩脆性不随岩样尺度变化而发生显著变化。

4.2 应力应变曲线

巴西劈裂试验中，不同尺度页岩岩样的应力应变曲线特征如图9 所示（图9 中，L'1，L'2，…，L'11分别为岩样C1，C2，…，C11 的长度，mm）。

图9 巴西劈裂试验得到的应力应变曲线的特征Fig.9 Characteristics of stress-strain curve obtained from Brazilian splitting test

由图9 可知，不同尺度页岩的峰前变形均经历了应力平行段、上凹段和线性变形段等3 个阶段。忽略由于微缺陷不均匀分布、扩展而引起的应力扰动，页岩巴西劈裂试验得到的典型应力应变曲线可分为以下3 种形态，如图10 所示。

图10 巴西劈裂试验得到的3 种典型的应力应变曲线Fig.10 Three typical stress-strain curves obtained from Brazilian splitting test

由图10 可知，页岩巴西劈裂试验的峰前变形不存在明显的塑性变形段，而是由线性变形直接进入脆性破坏，但在页岩初次线性变形与峰值强度之间，岩样变形共有3 种情况：1）由小斜率线性变形变为大斜率线性变形，如C3，C4，C6，C8 和C10；2）以原线性变形继续延伸，如C1，C2 和C11；3）由大斜率线性变形变为小斜率线性变形，如C5，C7 和C9。大多数岩样存在应力残余段，但岩样C1，C7，C8 和C11 却不存在。这都说明，巴西劈裂试验中页岩应力应变曲线分段变形特征离散性强，形态多样，其与尺度的关系比较复杂。

4.3 破坏形态

不同尺度页岩岩样巴西劈裂试验中的岩样破坏形态如图11 所示[13]。

图11 巴西劈裂试验的岩样破坏形态Fig.11 Failure forms of rock samples obtained from Brazilian splitting test

由图11 可知，页岩岩样主要以拉伸破坏为主，这是由巴西劈裂试验的特点所决定的，部分岩样除产生沿中轴方向的拉伸破坏外，还有沿其他方向的破坏，如沿层理面方向的破裂等。岩样C2 和C5 未沿中轴方向破裂，说明此时岩样沿非中轴方向的力学结构更加不稳定。但整体而言，页岩巴西劈裂仍以拉伸破坏为主，破坏形态不存在尺度效应。

5 不同加载方式下强度与变形尺度效应对比

5.1 显著性对比

由于页岩应力应变曲线和破坏模式无法精细定量表征，因此仅对比强度与变形参数尺度效应的显著程度，评价指标有2 个：1）具有显著尺度效应的力学参数数目；2）各参数与尺度关系拟合的决定系数R2。评价标准为：当具有显著尺度效应的力学参数越多，R2值（从大到小依次对比）和平均值越大，则该加载方式下页岩强度与变形参数的尺度效应就越显著。根据图1（高径比大于2.0 区间）、图5和图8 中数据，可得3 种加载条件下页岩强度与变形参数尺度效应显著性的对比结果（见表1）。由表1 可看出，页岩单轴压缩时强度与变形参数的尺度效应最为显著，巴西劈裂次之，三轴压缩时最不明显。

5.2 机理分析

上述分析表明，岩样高径比小于2.0 时，端部摩擦效应会显著影响页岩强度与变形的尺度效应；而高径比大于2.0 时，非均质性和各向异性则成为影响页岩强度与变形尺度效应的主导因素。

表1 尺度效应显著性对比结果Table 1 Comparison on the significances of scale effect

5.2.1 非均质性

单轴压缩试验和三轴压缩试验得到的页岩强度、变形与尺度的关系及尺度效应的显著性存在明显差异，其根本原因是，2 种加载方式下页岩沿加载方向的非均质性不同（见图12）。

图12 页岩单/三轴压缩时内部缺陷示意Fig.12 Schematic diagram of internal defects in shale under uniaxial/triaxial compression

由图12 可知，页岩单轴压缩时，由于未受到围压作用，岩样层理面内缺陷、贯穿层理面缺陷及局部微缺陷的尺度和张度均较大，致使页岩在沿垂向加载方向上具有极强的非均质性；且岩样尺度越大，岩样内出现尺度和张度较大缺陷的数目越多、概率越高，岩样非均质性越强。因此，单轴压缩时页岩强度与变形参数具有显著的尺度效应。但三轴压缩时，岩样围压为20 MPa 条件下，页岩内部各类缺陷在强外力作用下变得致密而均匀，此时页岩非均质性大幅下降，因此其强度与变形参数的尺度效应也随之减弱。

5.2.2 各向异性

页岩层理面为弱结构面，胶结作用弱，微缺陷发育，页岩沿层理方向的非均质性明显大于垂直于层理方向的非均质性，即页岩非均质性存在显著的各向异性特征。单轴压缩时，页岩所受外力方向与其层理方向平行，此时页岩非均质性被充分释放；巴西劈裂时，页岩外力方向与层理面方向垂直（见图13），此时岩样沿加载方向的非均质性较弱，因此相较于单轴压缩，页岩巴西劈裂时的强度与变形参数的尺度效应相对不明显。试验结果表明，巴西劈裂时岩样强度与变形参数的尺度效应比三轴压缩试验时显著，说明巴西劈裂试验中页岩沿加载方向的非均质度要强于三轴压缩试验。目前，数值模拟时，可以通过定义沿加载方向的非均质度来模拟加载方式对岩石强度与变形尺度效应的影响，但在物理模拟试验中，表示和测试岩石沿加载方向的非均质度还存在困难，仍需继续研究。

图13 页岩巴西劈裂试验原理及外力加载特征Fig.13 Principle of shale Brazilian splitting test and the characteristics of external force loading

综上所述，非均质性、各向异性和端部摩擦效应，是不同加载方式下页岩强度与变形尺度效应出现差异的根本原因，区别在于不同尺度范围和加载方式下，发挥主导作用的因素不同。因此，在利用室内岩石力学试验结果来指导工程实践时，必须明确加载方式对页岩强度与变形的尺度效应的影响，对于在特定尺度和加载方式下测定的页岩力学参数，必须经过校正才能应用于现场。