MATLAB和指数平滑法在福建省人口老龄化中的运用

黄 昱，刘金福，尤添革，周铮雯

（1.福建农林大学 计算机与信息学院，福建 福州 350002；2.福建农林大学 海峡自然保护区研究中心，福建 福州 350002；3.生态与资源统计福建省高校重点实验室，福建 福州 350002）

随着经济快速发展，人口老龄化成为当代中国所面临的一个严重社会问题，即社会养老保障、劳动力的减少、消费与储蓄等方面产生影响[1]，进而可能对社会稳定发展带来一定负面影响。

福建省于21世纪初进入老龄化社会，是目前人口的净输入省份，对其人口老龄化有一定的延缓作用，人口老龄化进程略低于全国平均水平[2]，原因主要是福建省经济发展相对较快，吸引了大量省外人口迁移流动，特别是劳动年龄人口的不断迁入，延缓了人口老龄化的进程。

1 研究区现状

从福建省六次人口普查数据看老龄化形势，福建省老龄人口基数较大且加速增长。老龄人口比重从第四次人口普查（1990年）时的5.07%到第五次人口普查（2000年）时的6.69%，平均每年上升了0.17个百分点。2015年全省的老龄人口比重达到8.45%，比2010年上升了0.56个百分点，也超过国际老龄化标准1.45个百分点，超过同期中国老年系数平均水平（8.10%）0.35个百分点（表1、图1）。

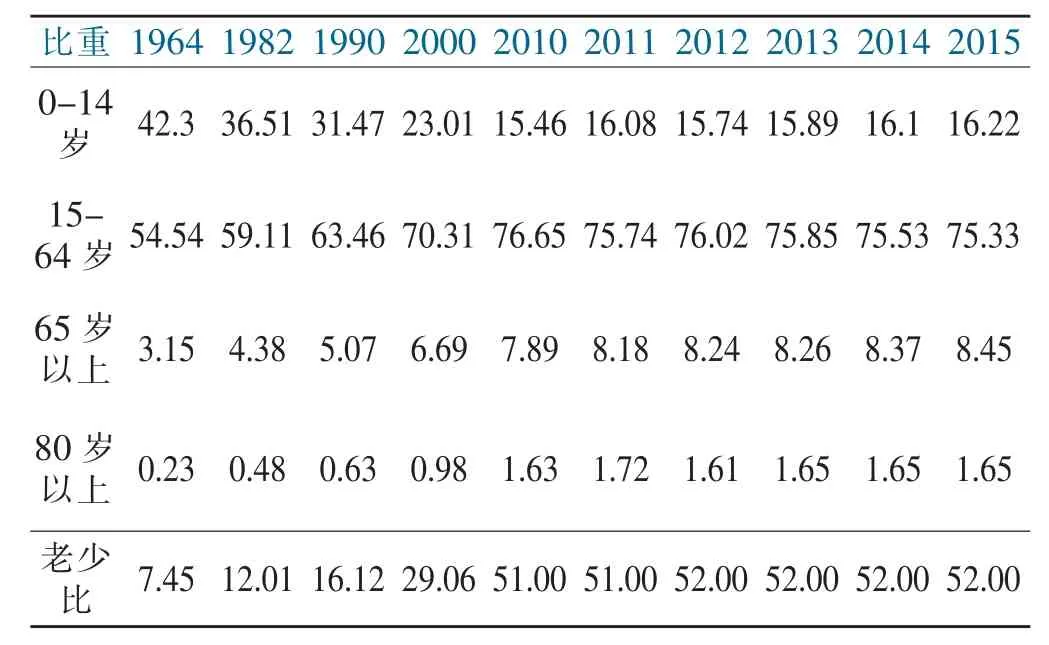
表1 福建省第六次人口普查年龄构成Tab.1 Age composition of the sixth population census in Fujian Province %

图1 福建省1953—2018年人口数占比Fig.1 Proportion of the population of Fujian Province from 1953 to 2018

对比2010年以后，2010—2018年，65岁及以上人口的比重上升1.11个百分点，可见随着时间增长，福建省老年人口越来越多，逐步进入老年化社会。

2 数据来源与预测模型

采用数据来源于福建省统计局（http://tjj.fj.gov.cn）及福建省统计年鉴，参考《2015年福建省1%人口抽样调查分析报告》的数据资料。采用65岁及以上的老年人口数，通过MATLAB的ARIMA模型及指数平滑法对福建省老年人口数进行建模分析，预测未来10 a的福建省老年人口数，比较2个的精准性。

3 ARIMA模型预测

3.1 ARIMA模型原理

ARIMA模型，也称为Box-Jenkins模型，是由Box和Jenkins在70年代初创立的一种时间序列建模方法[3]。ARIMA是最常见的预测模型，它是由自回归、滑动平均和差分变换3部分组成。

ARIMA（p,d,q）模型中的d为时间序列成为平稳时所做的差分次数。AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数[4]。

（1）阶数为p的AR模型的算法方程

式中：yt表示样本值，φi(i=1,2,…,p)表示AR(p)的参数，at表示白噪声序列。

（2）阶数为q的MA算法方程

式中：yt表示样本值，θi(i=1,2,…,q)表示MA(q)的参数，εt表示白噪声。

（3）一个ARMA(p,q)过程可以视为是AR(p)与MA(q)过程的迭加

式中：yt表示样本值，φi(i=1,2,…,p)和θi(i=1,2,…,q)表示ARMA(p,q)的两个参数，εt表示白噪声，且εt～N（0，σ2）。

3.2 建模步骤

（1）数据的平稳性检验

利用ARIMA模型建模必须确保数据具有平稳性，对序列平稳性检验有3种方法：第1种是时序图法，第2种自相关图法，第3种是构造检验统计量进行假设检验的方法，如ADF检验法(单位根检验)[5]。

（2）数据平稳性处理

采用d阶差分法对非平稳数据数据进行平稳化[6]，给定前一时间序列值｛xt｝（t=1,2,…,k），当前观察序列集为｛xt+1｝（t=1,2,…,k），一阶差分序列表示为：

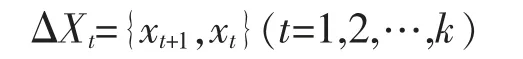
同理二阶差分方程可表示为：

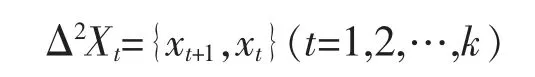
（3）模型定阶

根据差分次数确定参数d。根据自相关系数(ACF)和偏自相关系数(PACF)图、AIC或者BIC准则确定q,p阶数，一般常用的是利用AIC准则确定最佳模型阶数[7]。

（4）模型参数估计

采用最大似然估计或者最小二乘估计。

（5）残差白噪声检验

好的ARIMA模型尽量拟合线性成分，残差表现为白噪声。可对残差进行Q统计量和自相关图进行分析[8]。

检验统计量为：

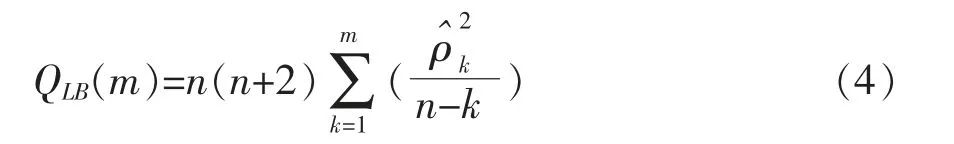
式中：ρΛ是k阶滞后的自相关系数的估计值，m为自相关系数的阶数(人为选定的一个数)，n是样本大小。

（6）对数据作出预测

（7）性能评估

3.3 结果分析

（1）数据的平稳性检验

采用2000—2018年共19个65岁以上人口数据进行建模预测，预测结果如图2、3所示。

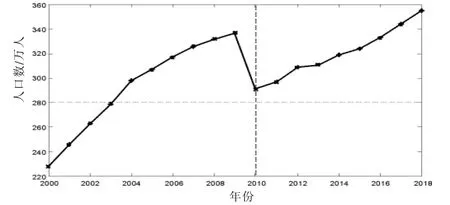
图2 数据时序图Fig.2 Data sequence diagram

图3 自相关和偏相关图Fig.3 Autocorrelation and partial correlation graphs

图2可看出从人口数是上下波动的，但是有明显的上升趋势性变化，因此可以大致判定老年人口数是非平稳的。老年人口数的ACF图呈现出自相关系数图呈现出倒三角状态，其因此可判断该时间序列是非平稳的（见图3）。

为了更加准确的判断数据的平稳性，接下来采用定量法——单位根检验法（ADF）来对老年人口数进行平稳性检验。由结果可知，t值均大于1%,5%,10%置信水平，拒绝原假设，即该序列为非平稳时间序列。

（2）数据平稳性处理

对老年人口数进行一阶差分处理的到的时序图如图4所示。

图4 一阶差分时序图Fig.4 First-order differential timing diagram

通过图4时序图观察法可以看出一阶差分后的序列无明显的趋势性变化，但是又有一定的下降趋势，因此无法准确判断差分后老年人口数的平稳性。

图5 一阶差分自相关图和偏相关图Fig.5 First-order differential autocorrelation graph and partial correlation graph

通过图5看出差分序列的自相关系数随着延迟阶数衰减向零的速度比较快，且表现出1阶截尾，因此一阶差分后的老年人口数是平稳的。

通过单位根(ADF)检验法一阶差分后数据的平稳性的判断后，发现t值均小于5%,10%置信水平，接受原假设，即一阶差分后的序列为平稳时间序列。通过时序图观察法和单位根(ADF)检验法都说明一阶差分后的序列为平稳时间序列。

（3）模型定阶

通过AIC准则可以得出,当阶数p=1,q=0的时候，AIC有最小值。因此确定ARIMA模型的最优阶数为p=1，q=0，d=1。即ARIMA（1,1,0）为最佳模型。

（4）模型参数估计

模型参数估计在MATLAB中有自带的库函数可直接调用。

（5）模型检验-残差分析

通过LB(Ljung-Box)检测统计量对残差数据进行检验。通过结果来看，显著性水平为0.05，前1～8阶的P值都显著大于0.05，那么相关系数与零没有显著差异，即时间序列中有用的信息已经被提取完毕，残差数据为白噪声序列，建模成功。

（6）数据预测

预测值如图6所示。

图6 福建省老年人口数预测Fig.6 Forecast of the elderly population in Fujian Province

从图6中可以看出，福建省老年人口数随着时间的推移，也逐渐增加，但是到了一定时期，老年人口数由于某些原因导致其减少，但是又逐步增加，其变化是不稳定的。

4 指数平滑法

4.1 指数平滑法原理

指数平滑法属于时间序列法中的一种，是由美国学者布朗（Robert G.Brown）于1960年提出的[9]，布朗认为时间序列的发展具有规律性、稳定性和规则性，能够合理地向外顺延。[10]根据平滑次数不同，指数平滑法分为一次指数平滑法、二次指数平滑法和三次指数平滑法等[11]。但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权数，新数据给予较大的权数，旧数据给予较小的权数[12]。

（1）指数平滑法基本公式

式中：St为时间t的平滑值；yt为时间t的实际值；St-1为时间t-1的平滑值；a为平滑常数，其取值范围为[0,1]。

（2）一次指数平滑法

当时间数列无明显的趋势变化，可用一次指数平滑预测[13]。其预测公式为：

（3）二次指数平滑法

二次指数平滑是对一次指数平滑的再平滑[14]，其预测公式为：

（4）三次指数平滑法

三次指数平滑预测是二次平滑基础上的再平滑。其预测公式为：

4.2 指数平滑法的预测

4.2.1 平滑系数的确定

当已知时间序列中的数据个数大于20时，可以近似认为初始值对未来预测值的影响较小，因此可考虑将目标序列的第一期数据作为模型初值。[16]当目标序列中的数值个数少于20，则可以取时间序列平均值作为当模型的初值。[17]初始值取平均值246，令a=0.3、0.6、0.9，进行一次指数平滑，结果如表2所示。

表2 一次平滑后老年人口数预测Tab.2 Forecast of the elderly population after a smoothing

由表2可看出，当a=0.9的时候，数值最接近真实人口数，故平滑系数取0.9。

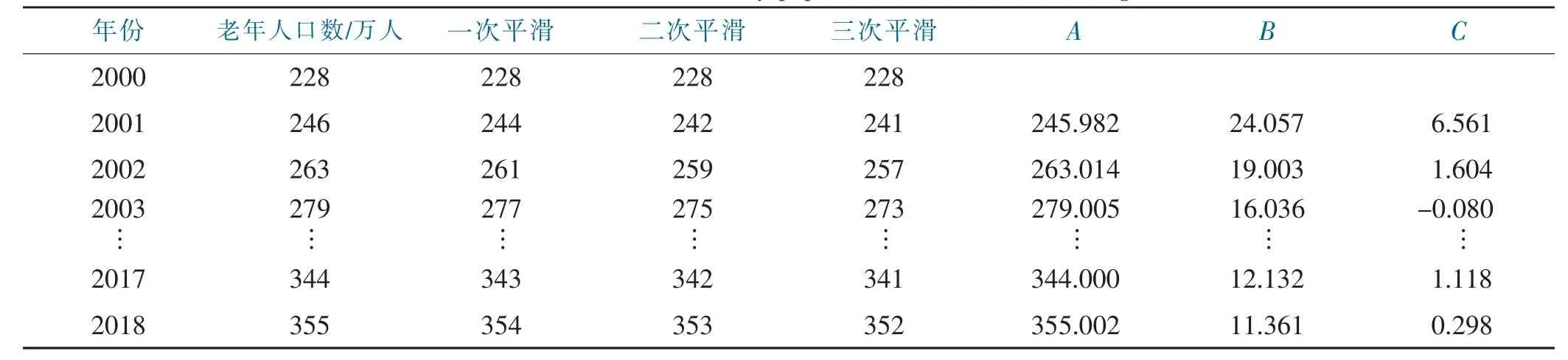
表3 三次平滑后老年人口数预测Tab.3 Forecast of the elderly population after three smoothing

4.2.2 模型确定

根据第一次指数平滑取得的平滑指数值，依次进行二次平滑和三次平滑，得出人口预测如表3所示。

综上所述，可以得出预测模型为Ft+m=At+Btm+Ctm2，即F2018+m=355+11.36m+0.298m2。

4.2.3 模型预测

通过预测模型，对福建省2019—2032年进行老年人口预测，得出的人口预测值见图7所示。

图7 福建省老年人口数预测图Fig.7 Forecast of the number of elderly in Fujian Province

从图7中看出福建省老年人口数随着时间的推移是在逐渐增加的。同理，对福建省总人口数同时进行三次指数平滑法，得出的预测模型为：F2018+m=3 941+27.969m-2.282m2，进行预测得出福建省总人口数预测。

图8中更能清晰发现随着年份的增加，老年人口数在总人口数当中的比例逐渐增加。

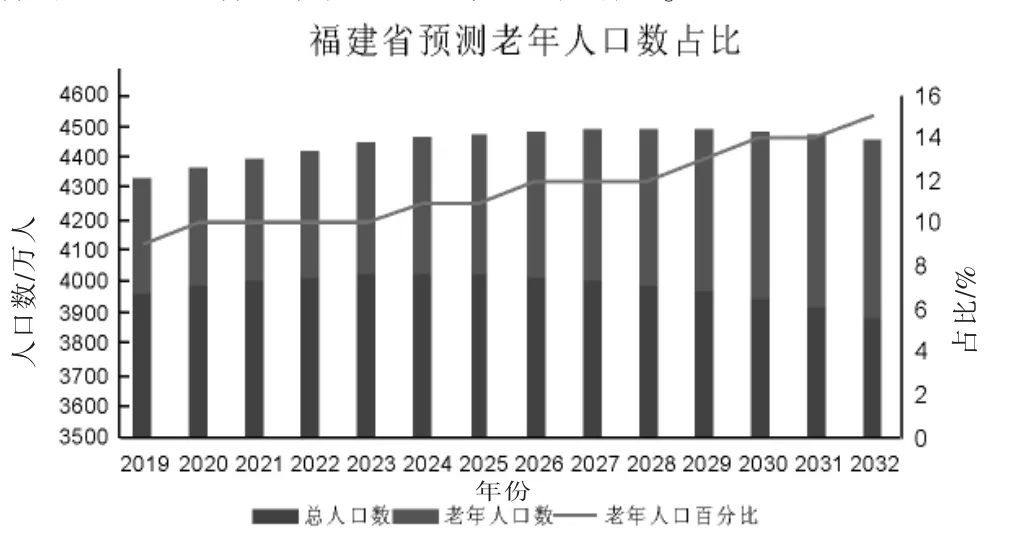
图8 福建省预测老人人口数占比Fig.8 Proportion of the population of the elderly in Fujian Province

从上述图表中可以看出，随着时间的变化，福建省老年人口数的比例虽有涨幅，但没有特别大的变化。

5 结论

研究通过分析福建省老年人口数，对人口老龄化进行了分析，通过建立ARIMA（1,1,0）模型和指数平滑模型，对福建省未来的老年人口数做了一个预测。研究发现福建省老年人口数呈现逐步上升的趋势，但是随着时间的延续，老年人口数又逐渐减少，呈现一种周期性。继而建立指数平滑模型F2018+m=355+11.36m+0.298m2，发现福建省老年人口数虽然呈现逐步增加的趋势，但趋势是平缓的。为了减缓进入老龄化社会的脚步，需要正确认识人口老龄化，抓住机遇，迎接挑战，积极采取相应的对策。[18]所以针对福建省人口老龄化，研究建议：

（1）实现健康老龄化，建立老年医疗健康保险制度

建立健全老年医疗健康保险制度是实现健康老龄化的现实路径。[19]老年人脱离工作岗位之后，大部分成为了弱势群体，而且老年人群是医疗保险的绝大部分人口，所以制定并完善医疗保险制度相关政策且建立医疗保障体系，改善老年人当前医疗条件水平。[20]

（2）构建老年人信息平台，鼓励用人单位对老年员工返聘

对于一些单位或者企业来说，老年员工拥有年轻员工所缺少的工作责任心，更重要的是拥有娴熟的知识理论和技能运用，所以政府可以搭建一个信息平台专门为老年人服务，并可以鼓励单位和企业对于老年员工进行返聘。

（3）促进构建养老保险制度体系框架

针对人口老龄化，政策设计者没有办法对其进行改变，但是他们能够制定合理的参数来平衡养老金的支出水平。这样不仅能为政府的财政负担减轻压力又能减少企业的缴费行为，并且能为老年人口提供充足的收入保障来避免出现老年贫困现象，最终达到长期财务收支平衡且能够可持续性的发展。