传感器数据异常下动力定位鲁棒状态估计方法
2020-12-03蒋帆,徐海祥*,2,冯辉,2,卜瑞波
蒋 帆, 徐 海 祥*,2, 冯 辉,2 , 卜 瑞 波
( 1.武汉理工大学 交通学院, 湖北 武汉 430063;2.武汉理工大学 高性能船舶技术教育部重点实验室, 湖北 武汉 430063 )
0 引 言
随着海洋作业的深入,传统的锚泊定位技术已经无法满足深远水域定位作业要求,动力定位(dynamic positioning,DP)技术以其不受水深限制、定位精度高且成本低、机动性强等独特优势应运而生,现已广泛应用于铺管船、科考船、海洋平台等海洋结构物的定位作业中[1-2].
动力定位船舶为了实现定位、循迹等作业,其控制系统需要实时获取准确可靠的船舶运动状态与外界环境信息.作为动力定位船舶的“眼睛”,状态估计的作用正是从携带噪声信号的观测数据中估计船舶运动状态.20世纪70年代,Balchen等[3]将卡尔曼滤波(Kalman filter,KF)引入动力定位中,KF的引入是动力定位系统发展的一个里程碑事件,它的出现宣告了在动力定位领域真正意义上基于模型的状态估计方法的诞生.但是无论是KF还是随后改进提出的扩展卡尔曼滤波(extended Kalman filter,EKF)都对于船舶的数学建模、外界环境干扰和传感器系统噪声的建模过于理想化,状态估计会产生一定误差.1999年,Fossen 等[4]将非线性无源滤波引入动力定位系统中,并利用无源理论和Lyapunov方法证明了滤波器的稳定性,但该方法的状态估计精度受波浪频率等参数的影响较大.为此,一些基于非线性无源理论的改进方法相继提出[5-9],这些方法通过调整增益矩阵以匹配复杂时变环境,但应用这些方法的前提都是传感器测量信号正常.然而在实际工程作业中,复杂时变的海洋环境、自然与人为的电磁干扰等都会导致传感器数据出现异常,进而影响状态估计的准确性和整个动力定位系统的稳定性,更有甚者会导致动力定位船舶发生碰撞、失控等事故.因此对于动力定位船舶而言,设计鲁棒的状态估计算法以处理传感器数据异常情况显得尤为关键.
无迹卡尔曼滤波(unscented Kalman filter,UKF)是针对非线性系统状态估计提出的滤波方法,其在动力定位系统状态估计的有效性已被国内外学者相继验证[10-13].然而UKF在处理传感器数据异常情况下的状态估计问题时,会导致滤波结果发散,难以达到满意的估计效果.针对上述问题,诸多学者采用故障诊断的方法对传感器故障类型、原因等进行诊断,最终结合容错控制给出相应的解决方案.传感器故障诊断由来已久,但是针对动力定位的方法却很少.文献[14]提出了一种基于神经网络预测器的传感器故障诊断方法,该方法首先对传感器数据进行卡尔曼滤波,随后利用神经网络进行故障诊断,由于类似卡尔曼滤波这些基于模型的滤波器会使含有异常传感器数据的滤波结果发散,因此这种“先滤波后诊断”的处理方式违背了自洽性原则,难以用于工程实际.文献[15]通过设计有限脉冲响应滤波器,并利用残差平方和判据与信噪比判据对船用罗经进行故障诊断,仿真结果验证该方法的有效性,然而采用信噪比判据会存在一定的滞后效应.事实上,动力定位系统对数据的实时性要求非常高,滞后效应对动力定位控制会产生不利影响.
鉴于此,一些学者另辟蹊径,将状态估计与传感器故障诊断相结合,保证在传感器数据异常情况下状态估计准确性和实时性.文献[16]就超微型卫星系统发生故障的情况提出了鲁棒自适应UKF,通过假设检验的方法检测故障的发生,再利用协方差匹配原理更新噪声协方差以匹配模型参数摄动以及传感器数据漂移带来的影响.文献[17]针对无人机出现传感器/执行器故障问题,提出了基于卡尔曼滤波和故障诊断的状态估计方法.动力定位系统是一个闭环反馈控制系统,传感器数据异常对动力定位系统的影响之大有别于其他开环系统(比如组合导航等),具体而言,传感器数据异常不仅影响动力定位状态估计的精度,还会导致控制系统产生错误的控制指令,而该控制指令又是下一周期状态估计输入的一部分,如此反复最终导致难以实现定位等作业要求.文献[18]提出了一种改进的UKF,利用观测噪声协方差矩阵R自适应更新处理动力定位船舶传感器数据出现离群值的问题,并通过仿真验证了方法的可行性,然而其研究只单独限于状态估计部分,缺乏整体性.
本文在上述研究的基础上,汲取文献[18]对观测噪声协方差矩阵R自适应更新的思想,提出一种鲁棒的无迹卡尔曼滤波方法,该方法通过引入一种基于指数加权的观测噪声协方差矩阵R自适应更新模块和一种基于卡方分布假设检验方法的过程不确定性识别模块处理传感器数据异常情况并估计未知环境力.最后以某平台供应船的船模为仿真对象,进行仿真对比实验.
1 数学模型
对于水面船舶而言,其运动包括6个自由度,即纵荡、横荡、垂荡、纵摇、横摇、艏摇.而动力定位船舶往往忽略垂荡、横摇、纵摇对水平面运动的影响,即只考虑3个自由度(纵荡、横荡、艏摇)运动.因此,针对动力定位船舶的非线性运动数学模型[19]可以表示为
(1)
式中:ξh为船舶高频运动位置与速度向量;Ah为赫尔维茨矩阵;Eh、Eb、Eυ都表示噪声的幅值矩阵;ηh为船舶高频运动位置向量;η为船舶低频运动位置向量;J(ψ)为坐标转换矩阵;υ为速度矩阵;b为环境力矩阵;Tb为时间常数矩阵;M表示船舶惯性矩阵;D表示船舶阻尼系数矩阵;τ为推进器产生的推力和力矩;ωh、ωb、ωυ、vy都表示零均值高斯白噪声;y为传感器观测位置;下标h、b、υ、y分别表示船舶高频运动、环境力、船舶低频运动以及传感器量测方程.相关矩阵的具体形式为


A22=-diag{2ζ1ω01,2ζ2ω02,2ζ3ω03};
Σ=diag{Kω1,Kω2,Kω3}
式中:ω0i(i=1,2,3)表示对应自由度的波浪谱谱峰频率;ζi(i=1,2,3)表示对应自由度的阻尼系数;Kω i(i=1,2,3)表示对应自由度的增益系数,Kω i=2ζω0iσi(σi为描述波浪强度的常量).
将式(1)写成状态空间模型:

(2)



2 无迹卡尔曼滤波
1995年,Julier等将无迹变换(unscented transformation,UT)的思想引入卡尔曼滤波中,提出了无迹卡尔曼滤波.与传统扩展卡尔曼滤波处理非线性系统状态估计问题的方式不同,UKF摒弃了对非线性函数进行线性化的传统做法,它不需要求导计算Jacobian矩阵而是用固定数量的参数去逼近状态的后验概率密度,由于没有将高阶项忽略,其估计精度较高且稳定性较强.因此,UKF被广泛应用于目标跟踪[20]、信号处理[21]和机器学习[22]等众多领域.

(1)sigma点采样与对应权值计算
(3)
(4)

(2)预测(时间更新)
(5)

(3)更新(测量更新)
(6)

3 观测噪声协方差矩阵自适应更新
当传感器数据出现异常时,由于传统UKF无法自适应更新观测噪声协方差会导致估计精度下降,为此本文设计了一种基于指数加权的观测噪声协方差矩阵R估计器.
首先,定义新息序列为
(7)
将式(2)中的观测方程代入式(7)并结合动力定位状态估计数学模型可得:
(8)
式中:xk为实际状态向量;vk为观测噪声向量.
定义误差向量Δxk为
(9)
易得:
(10)
式中:E(·)表示期望.由于新息序列具有弱自相关性(正交性),新息序列协方差矩阵可通过下式计算得到:
(11)
故观测噪声协方差矩阵可以表示为
(12)
对于新息序列协方差的估计,文献[11]采用算数平均法,其表达式为
(13)
式中:εi为第i时刻的新息序列.由于算数平均法只针对k时刻之前的新息序列协方差平方和进行算数平均作为k时刻新息序列协方差的估计值,对历史数据的利用程度都相同,新息序列协方差的估计精度会随周期数增加而下降[17].为此,本节设计了一种基于指数加权的新息序列协方差估计方法.
对于k时刻之前的新息序列协方差,其权重系数
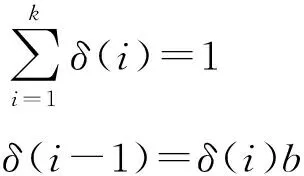
(14)
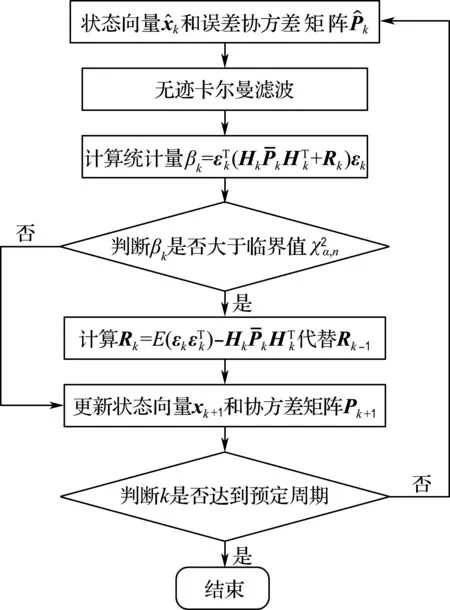
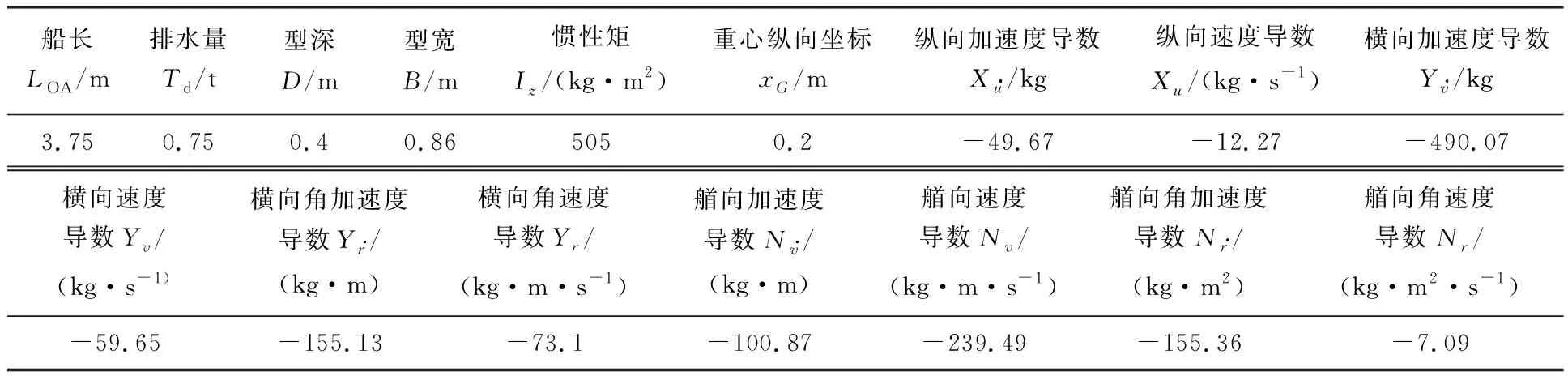
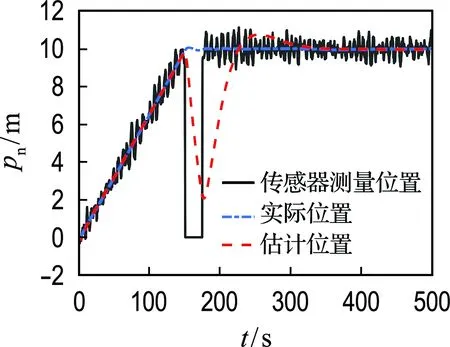
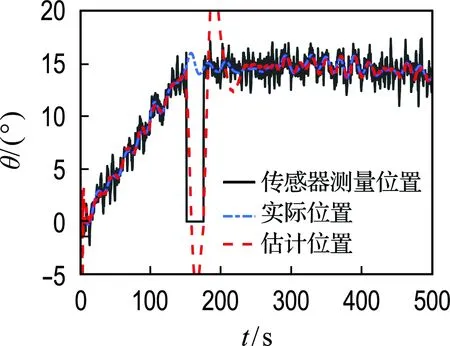
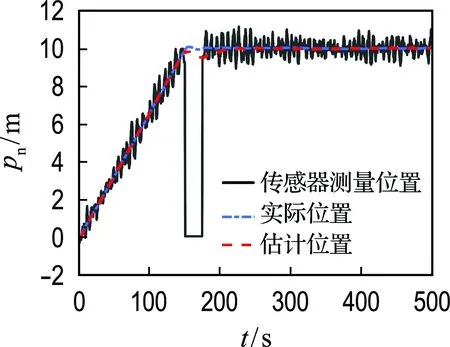
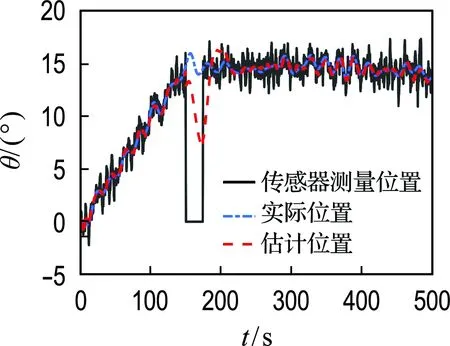
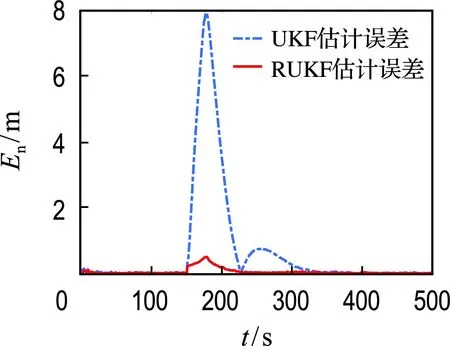
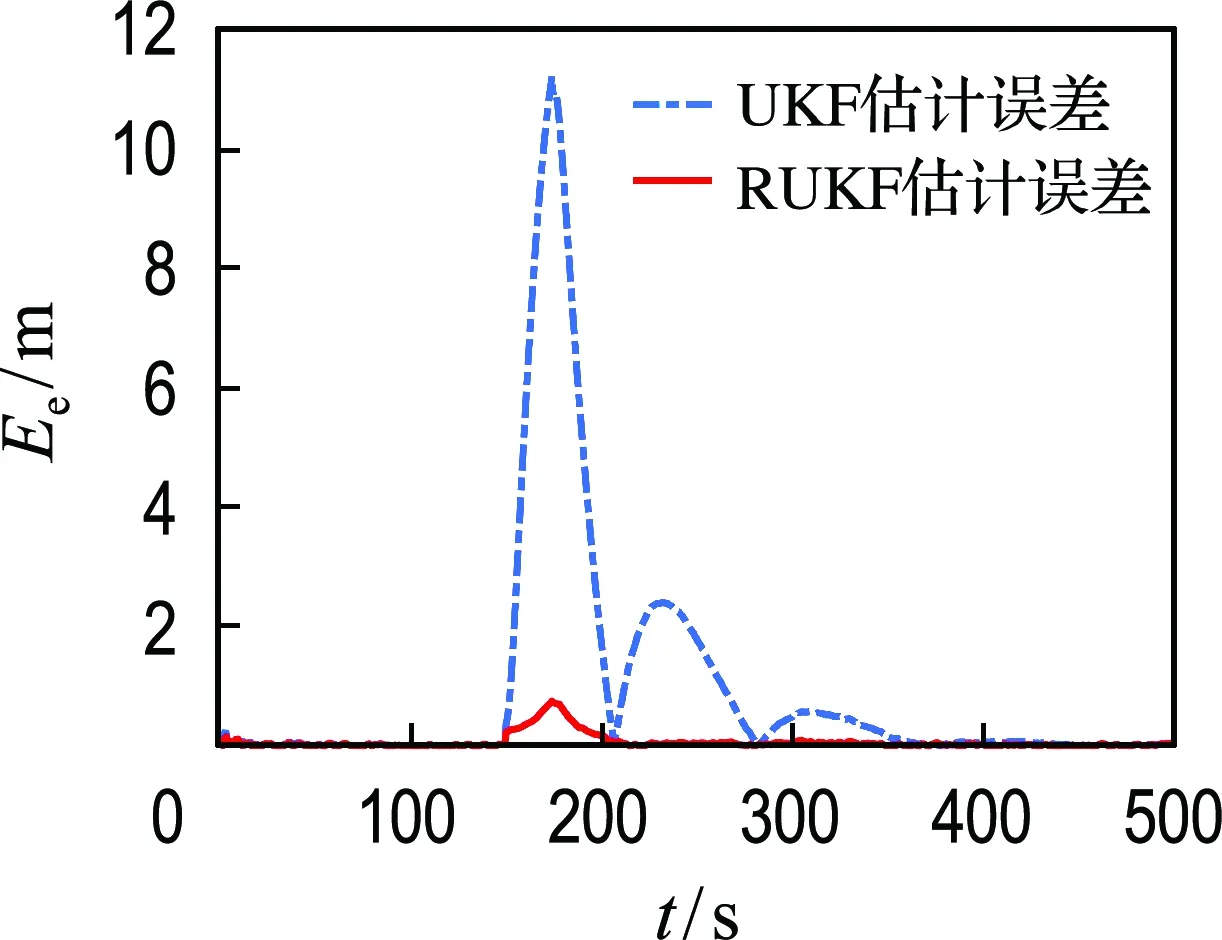
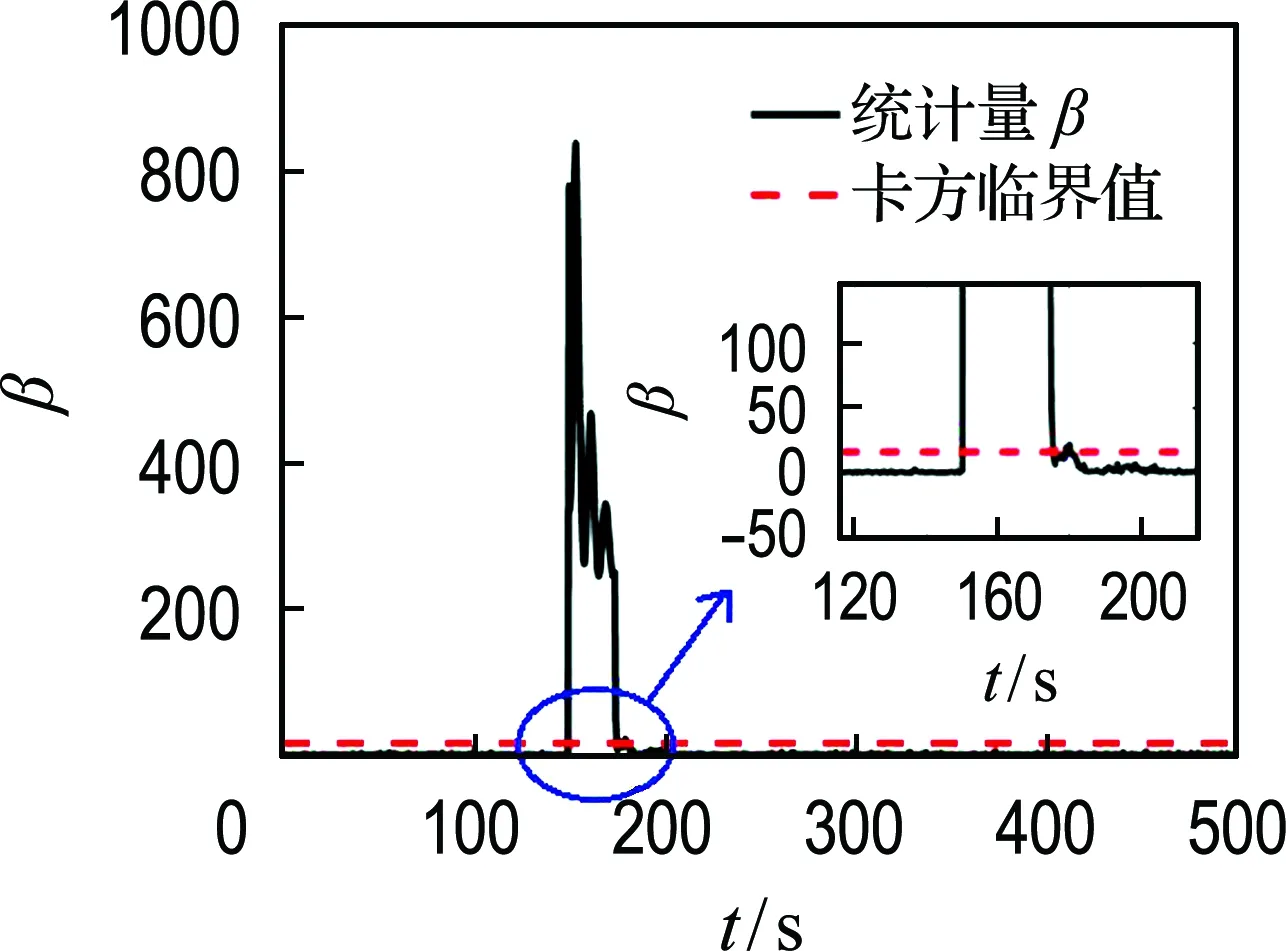
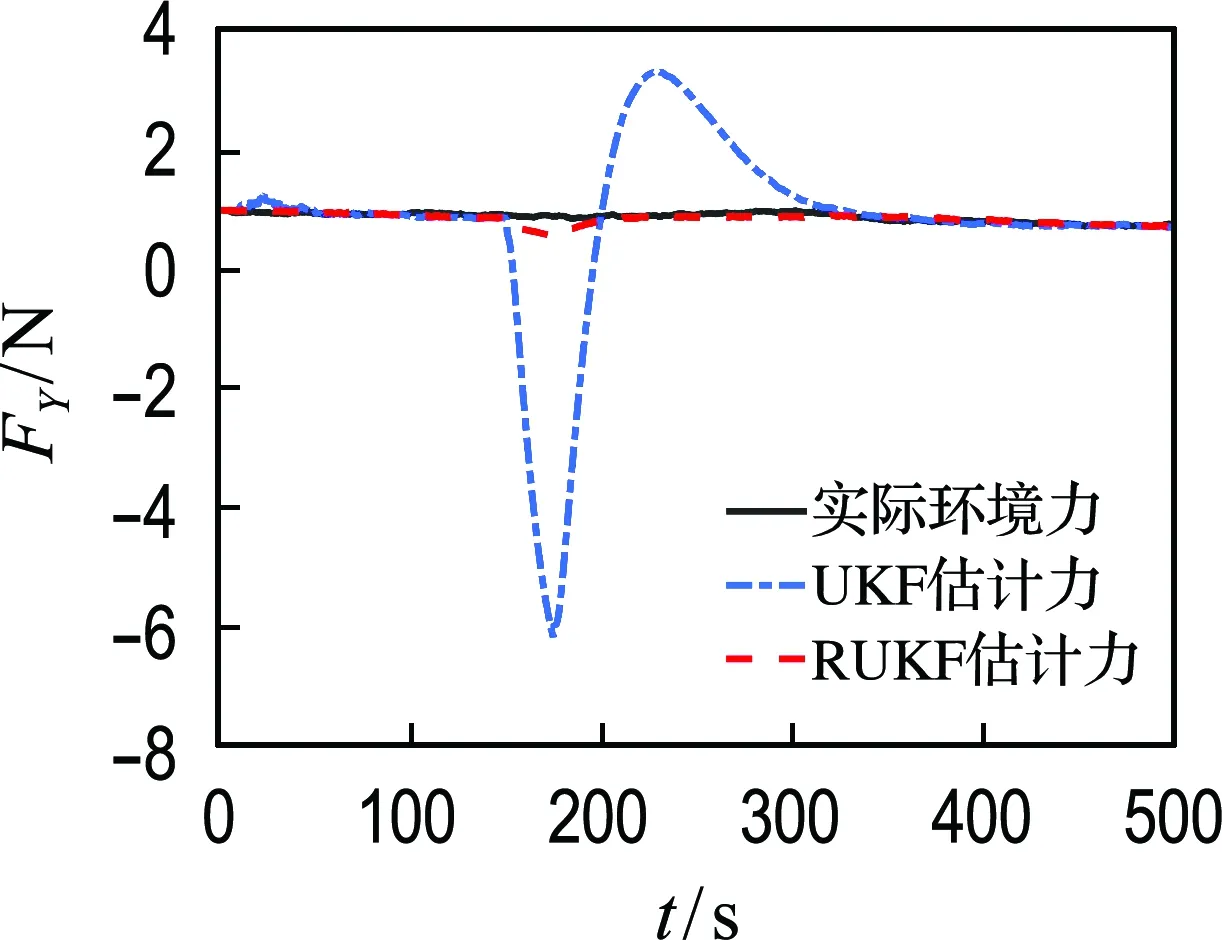
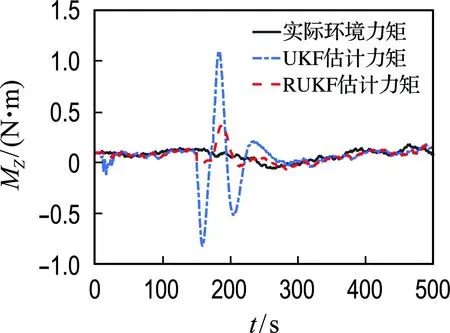
式中:δ(i)为第i时刻新息序列协方差的权重;b为渐衰因子,且满足0 式(13)可以转化为 δ(k)bk-1+δ(k)bk-2+…+δ(k)b+δ(k)=1 (15) 在渐衰因子b确定后,δ(k)就可以用含b的代数表达式表达,即 (16) 则第i时刻新息序列协方差的权重δ(i)可表达为 δ(i)=δ(k)·bk-i (17) (18) 由式(16)可得: (19) (20) 为了分析研究和传感器设备检修,动力定位系统往往需要明确传感器数据何时发生异常.为此,本文设计基于卡方分布的假设检验方法,用以对过程不确定性进行识别,且规定观测噪声协方差矩阵R只在传感器数据发生异常时进行自适应更新.具体过程如下: 首先,提出两种假设: 假设1零假设γ0:传感器数据正常; 假设2替代假设γ1:传感器数据异常. 其次,通过形如下式的统计量检测传感器数据异常: (21) 结合上述内容,基于鲁棒无迹卡尔曼滤波的动力定位船舶状态估计整体过程如图1所示. 图1 鲁棒无迹卡尔曼滤波的状态估计流程 为验证时变环境下鲁棒无迹卡尔曼滤波(robust unscented Kalman filter,RUKF)在估计环境扰动方面的有效性和处理传感器数据异常情况的优越性,设计了仿真对比实验,仿真实验在相同硬件设备(Windows 7旗舰版)和相同程序编译平台(MATLAB 2014b)条件下进行. 仿真实验以一艘缩尺比为1∶20的平台供应船的模型为对象,与模型相关的船模参数、水动力导数如表1所示. 船舶数学运动模型中相关参数的选取如下:ω0i=0.8 rad/s (i=1,2,3),ζi=0.3 (i=1,2,3),σi=1.04 (i=1,2,3). 为模拟时变环境力,时间常数矩阵Tb取为 3个自由度(纵荡、横荡和艏摇)上的观测噪声协方差矩阵R为 表1 平台供应船模型相关参数 过程噪声协方差矩阵Q=diag{0,0,0,0.1,0.1,0.000 1,0,0,0,0,0,0,0.000 1,0.000 1,0.000 1}. 为模拟闭环控制系统兼顾动力定位系统各个模块的整体性并使船舶保持在定位点,仿真采用PID控制器模拟产生每一周期的控制力,控制器的设计如下: (22) 船舶初始位置设置为[0,0,0],定位点位置设置为[10 m,10 m,15°],采样周期为0.5 s,仿真时长为1 000个周期. 为验证传感器数据异常情况下鲁棒无迹卡尔曼滤波的优越性,仿真中在第300~350个周期(150~175 s)时将式(2)中的传感器观测值置零来模拟传感器数据异常情况. 仿真结果如图2~4所示. (a) 北向位置变化 (b) 东向位置变化 (c) 艏向角度变化 图2为采用UKF时,船舶北向、东向和艏向的传感器测量位置、实际位置以及估计位置变化图.图3为采用RUKF时,船舶北向、东向和艏向的传感器测量位置、实际位置以及估计位置变化图.从图中可以看出,UKF和RUKF最终都能使船舶到达目标点实现定位功能,但在150~175 s期间传感器数据出现异常的情况下,UKF对船舶位置与姿态的估计产生较大的偏差且其估计精度受影响的时间要比发生异常的时间更长,与UKF相比,RUKF虽然在数据异常期间估计精度也有所下降,但其下降幅度远低于UKF,且数据异常后能更快恢复其估计精度,从而更为平稳、更为快速地到达目标位置. (a) 北向位置变化 (b) 东向位置变化 (c) 艏向角度变化 图4为UKF和RUKF的船舶北向、东向和艏向估计误差变化对比图.从图中可以看出,在传感器数据出现异常时,RUKF的估计误差远低于UKF,且其能在更短的时间恢复到未出现数据异常时的估计精度. 图5为过程不确定性识别模块卡方分布假设检验统计量β变化图.从图中可以看到,当传感器数据出现异常时,统计量β迅速增大并超过卡方临界值,此时替代假设γ1成立,这充分验证了提出的基于卡方检测的过程不确定性识别方法的有效性. (a) 北向位置估计误差 (b) 东向位置估计误差 (c) 艏向角度估计误差 图5 卡方分布假设检验统计量β变化 图6为UKF和RUKF对X、Y、Z3个方向未知外界环境力(矩)的估计对比图.由图可知,UKF在传感器数据出现异常时且在之后较长一段时间内对环境力(矩)的估计精度明显下降,而RUKF仍能保持较高的估计精度. (a) X方向外界环境力估计对比 (b) Y方向外界环境力估计对比 (c) Z方向外界环境力矩估计对比 综合上述分析可知,对UKF而言,传感器数据出现异常会导致状态估计(包括位置姿态以及外界环境力)精度下降从而使控制系统产生有偏差的控制指令,该控制指令又作为下一周期状态估计的输入,造成误差累加,而最终能达到定位点完成定位工作得益于PID控制器“利用偏差以消除偏差”的工作原理.对RUKF而言,由于过程不确定性识别模块的加入,能够准确及时地识别传感器数据何时发生异常,又通过观测噪声协方差矩阵R的自适应更新,提高了状态估计精度,加快了收敛速度,表现出很好的鲁棒性.因此,RUKF更适用于动力定位实际工程应用. 本文针对时变环境下动力定位船舶由于未知环境干扰、传感器数据异常的问题而无法准确及时地得到船舶位置、姿态与外界环境干扰信息的问题,提出了一种鲁棒无迹卡尔曼滤波方法.针对传统无迹卡尔曼滤波无法自适应更新观测噪声协方差的缺陷,设计了基于指数加权的观测噪声协方差矩阵R估计器.在此基础上,引入了基于卡方分布的假设检验方法用以确定传感器数据发生异常的时刻.最后,设计了仿真对比实验,验证了所提出的状态估计方法的有效性和优越性.
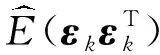
4 过程不确定识别

5 仿真实验与结果分析


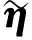




6 结 语
