基于发动机怠速工况的悬置系统振动特性研究

刘通 刘艳华 赵晓亮

（华晨汽车工程研究院）

现阶段在乘用车领域，人们对于乘坐舒适性的关注度逐渐提高，由于发动机激励引起的车身端振动以及对悬置自身隔振能力[1]的评价至关重要。考虑到由发动机传递出振动到车身端的路径并不唯一，因此如何搭建符合实际状态的整车模型以及发动机激励的建立，都是当前行业内讨论的热点与难点之一。大多数研究者在进行振动分析[1-5]时，只是简化模型，单纯考虑垂向传递路径，没有将悬弹性元件对振动的贡献度体现出来。基于此，以某项目实际结构为依据，建立了37 自由度整车模型并根据发动机活塞做功原理建立驱动激励；针对整车振动NVH 问题进行线性刚度优化；基于怠速工况进行隔振[6]以及悬后振动分析与方法研究。通过与实际测试数据对比，验证了模型的准确性，这对于悬置系统后期调校和NVH 品质提升都具有一定的指导意义。

1 整车模型建立

基于整车考虑悬置系统振动，要想得到近似真实的仿真数据，需要建立复杂的振动系统，演变过程如下。

动力总成悬置系统可以简化成弹簧与刚体构成的6 自由度系统，其动力学方程，如式（1）所示。

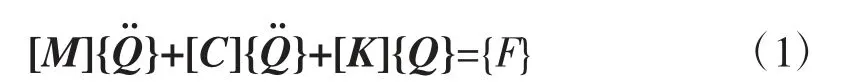
式中：[M]——动力总成质量矩阵；

{Q}——动力总成位移矩阵；

[C]——悬置阻尼矩阵；

[K]——悬置刚度矩阵；

{F}——激励力矢量。

质量矩阵为动力总成质量惯量矩阵，如式（2）所示。

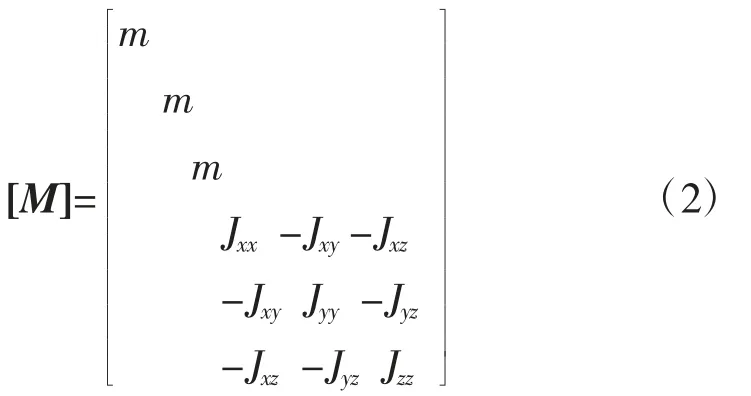
式中：m——动力总成质量，kg；

Jxx，Jyy，Jzz——绕坐标轴的惯性矩；

Jxy，Jxz，Jyz——绕坐标轴的惯性积。

系统总刚度矩阵[K]的表达式，如式（3）所示。

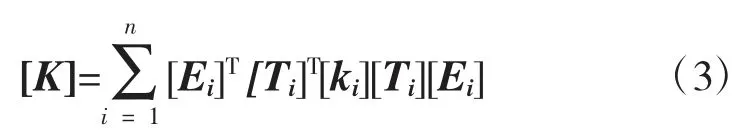
式中：[Ei]——坐标变换矩阵；

[Ti]——角度变换矩阵；

[ki]——每个悬置的刚度矩阵。

对式（1）求解，得到悬置系统6 阶圆频率ω1～ω6，及振型向量{Qi}。

在此基础上，增加车轮与车身，构成13 自由度模型，如图1 所示。

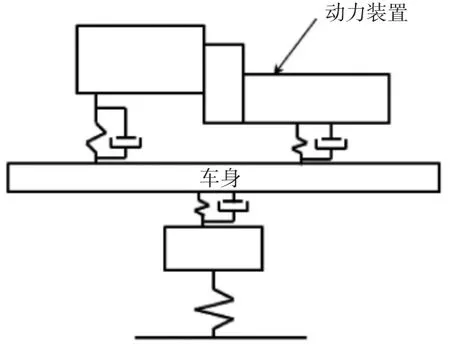
图1 13 自由度模型示意图

这里虽引入车身与轮胎自由度，但发动机激励并不向单一方向传递，因此13 自由度模型对于分析振动问题还不够精确。

为全面分析悬置与发动机和车身三者之间振动的传递关系，基于上述模型进一步增加减振器、弹簧、转向节、下摆臂等部件，车身只考虑z向、侧倾、俯仰3 个自由度，这样发动机传递到车身的振动构成闭环，更真实准确。经过计算，总共为37 自由度模型，如图2所示。

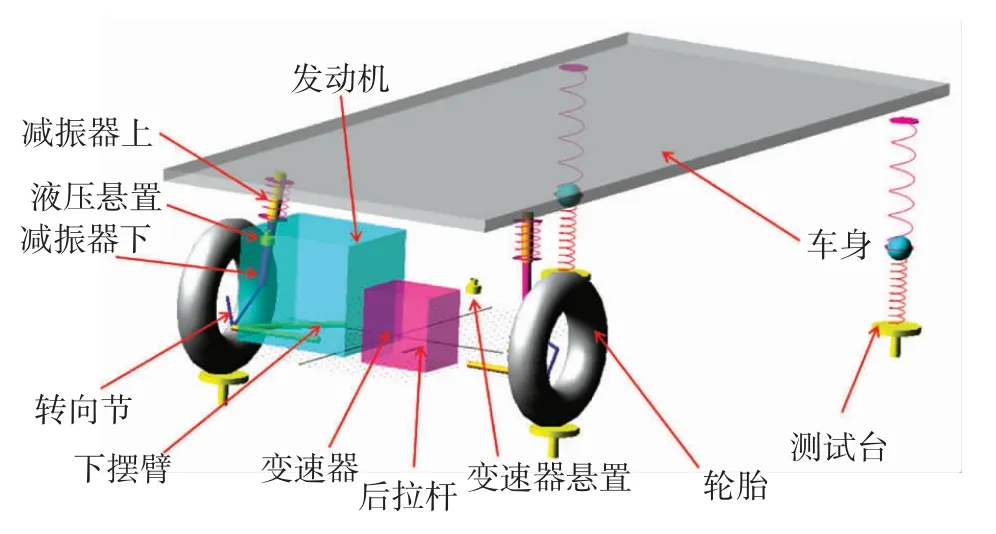
图2 考虑悬架因素的整车模型

其中各零部件自由度和约束与实车一致，具体如表1 所示。

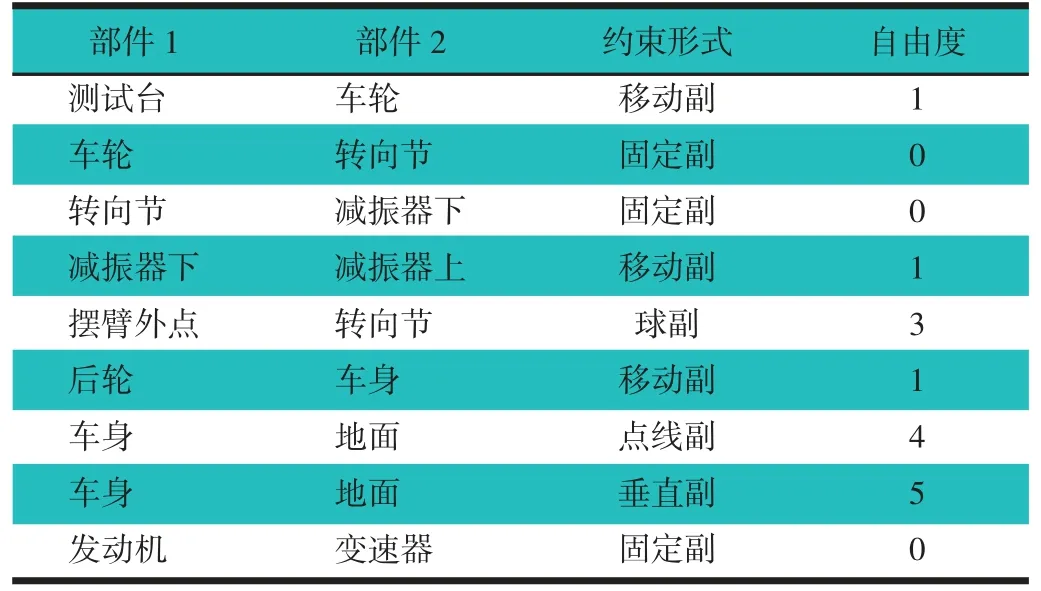
表1 各零部件之间约束

2 发动机怠速激励分析

四缸发动机激励可以看成单缸发动机激励的叠加，由于每个缸的运动时间不同，因此会产生持续往复运动。其单缸发动机曲柄连杆机构运动学及受力，如图3 所示。

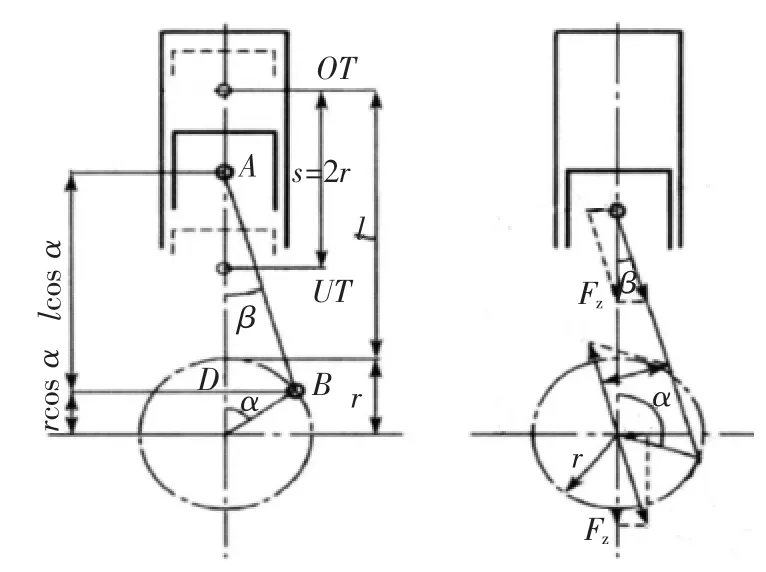
图3 发动机运动与作用力描述

四缸发动机激励表达式[7]，如式（4）和式（5）所示。

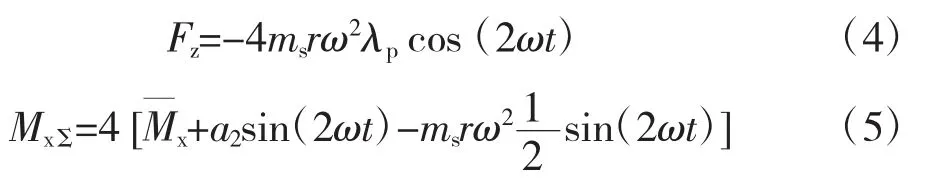
式中：Fz——垂向力，N；

MxΣ——倾覆力矩，N·m；

——活塞上的气体平均扭矩，N·m；

r——曲柄半径，mm；

λp——半径与连杆长度l之比；

ω——曲轴角速度，rad/s；

ms——往复运动等效质量，kg；

a2——正弦波成分对应的幅值，N·m。

文章基于某款四缸直列发动机参数：ms=0.494 kg，r=44 mm，l=140.7 mm，=68.7 N·m，该发动机怠速转速为750 r/min，最大扭矩为210 N·m；最后，基于发动机激励力理论公式，建立驱动模型，将垂向驱动与力矩驱动施加到动力总成质心处，完成驱动建模，如图4 所示。

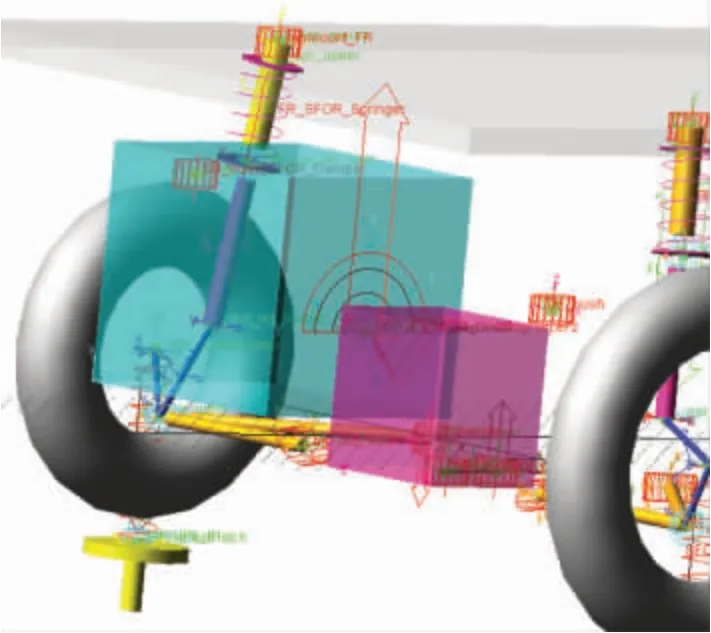
图4 发动机驱动的建模截图

3 振动分析与讨论

3.1 线性刚度调试

振动调试的基础首先要保证悬置各个方向的解耦[8]。某项目车型在调校过程中，虽然悬置系统刚度基本满足解耦率及频率分布的要求，但是在整车怠速工况下振动存在耦合，并不理想。

该悬置系统样件刚度数据，如表2 所示。

表2 某车型动力总成各悬置刚度N/mm

通过对整车模型进行模态分析，得到了该车型悬置系统基于系统模态和整车模态的对比图，如图5 所示。

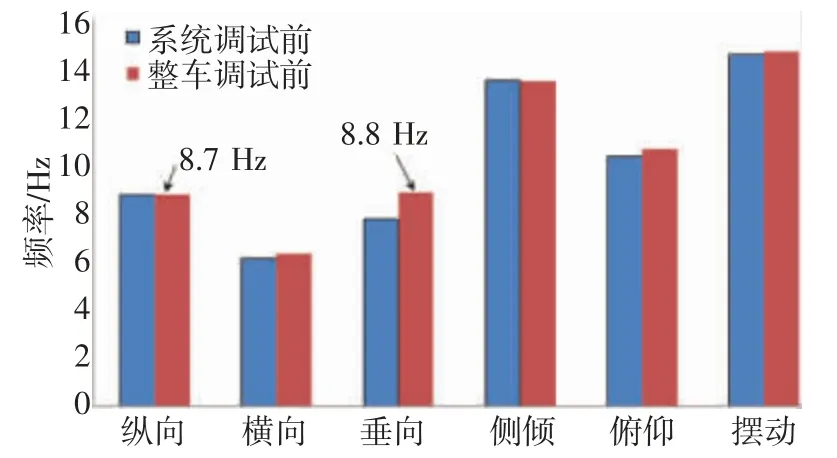
图5 某车型悬置系统刚度优化前模态对比

由图5 可知，基于整车的悬置模态与系统级别相差不大，但是可以看到整车纵向模态频率为8.7 Hz，垂向模态频率为8.8 Hz，二者几乎频率重叠，非常容易耦合，这也会间接使得在整车环境下NVH 测试指标不达标。而这在系统级别频率分布上是满足1 Hz 间隔要求的。

为解决整车状态下纵向与垂向模态的耦合问题，对悬置系统刚度进行优化，如表3 所示。

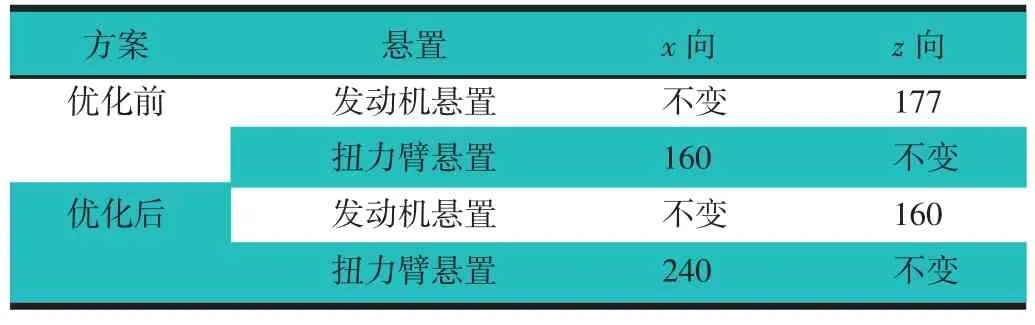
表3 各悬置刚度优化过程 N/mm

基于优化后刚度，通过仿真计算，系统模态与整车模态对比，如图6 所示。

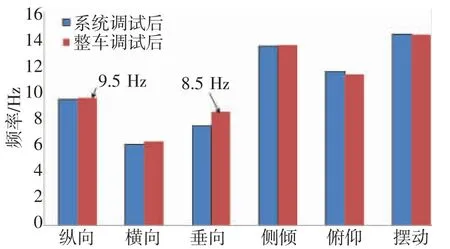
图6 某车型悬置系统刚度优化后模态对比

由图6 可知，调整后各主方向模态频率都满足了要求，特别是纵向频率由8.7 Hz 上升到9.5 Hz，垂向频率由8.8 Hz 降低到8.5 Hz。振动耦合得到规避，实车状态更好，为隔振分析排除了耦合振动因素。

3.2 隔振分析

基于振动传递率的振动分析[9]是为了体现在动态激励状态下每个悬置的隔振能力，找到影响隔振指标的因子，从而逐步完善对零部件的调校工作。

隔振分析基于Bode 图算法计算而来，Bode 图是系统频率响应的一种图示方法，利用Bode 图可以看出不同频率下，系统增益的大小及相位。

通常用传递率来评价悬置工作效果，其使用加速度的传递率表达式，如式（6）所示。

式中：Tdb——振动传递率；

aa——输出加速度，mm/s2；

ap——输入加速度，mm/s2。

如果仿真结果为负值，只是方向问题，并无实际意义。

3.2.1 橡胶件刚度转化

为提高仿真的精确度，模型里需要定义每个悬置激励频率下对应的刚度和阻尼。根据橡胶本身的结构特性，有如下公式：

式中：Fd——阻尼力，N；

k——静刚度，N/mm；

d——阻尼，Ns/m；

x——运动位移，mm。

基于式（7）进行拉式变换，整理得到：

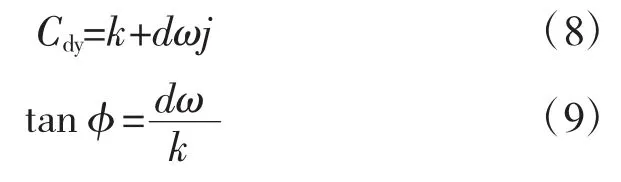
式中：Cdy——动刚度，N/mm；

φ——损失角，（°）。

通过试验测试曲线，选取振幅为0.1 mm 的工况，并读取25 Hz 频率下的动刚度等信息。经过计算，左右悬置各测试参数转化，如表4 所示。

表4 怠速工况下刚度及损失角转化

通过转化，将静刚度与阻尼代入悬置橡胶衬套模型，以此来真实反映怠速时橡胶刚度的状态。后悬z向并非主方向，这里静刚度取自身解耦刚度，阻尼取0。

3.2.2 结果讨论

由于激励引起的振动主方向为垂向，故文章主要探究垂向系统振动特性，并在仿真中以EM，TM，Tq 分别代表发动机悬置、变速器悬置和扭力臂悬置名称。经过仿真，各悬置隔振指标，如图7 所示。怠速激励频率为25 Hz，在此频率下各振动指标均大于20 dB，即满足隔振要求。

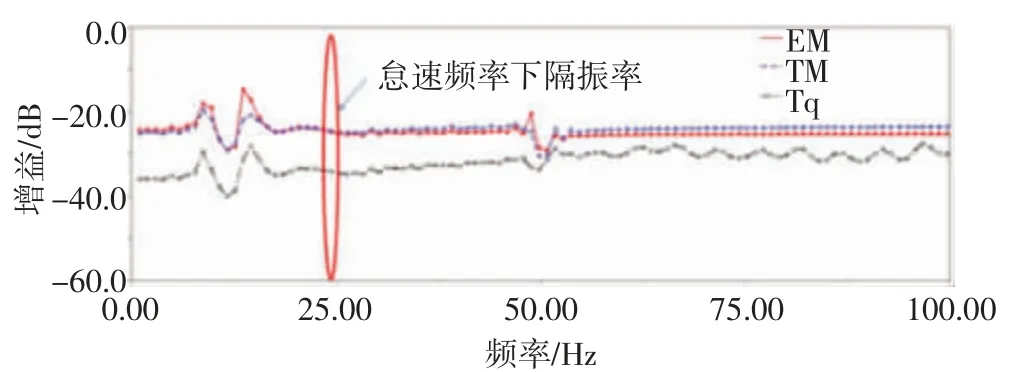
图7 各悬置怠速工况下隔振值

另外，除了用隔振量表达悬置本身的衰减振动能力，还需考察车身端悬置的振动峰值，如果悬后振动不理想，驾驶员与乘客主观体验也会受到很大影响。

为此，基于发动机激励输入，通过仿真对比了3 个悬置的悬后振动[10]峰值，时域曲线与频域曲线对比，如图8 和图9 所示。

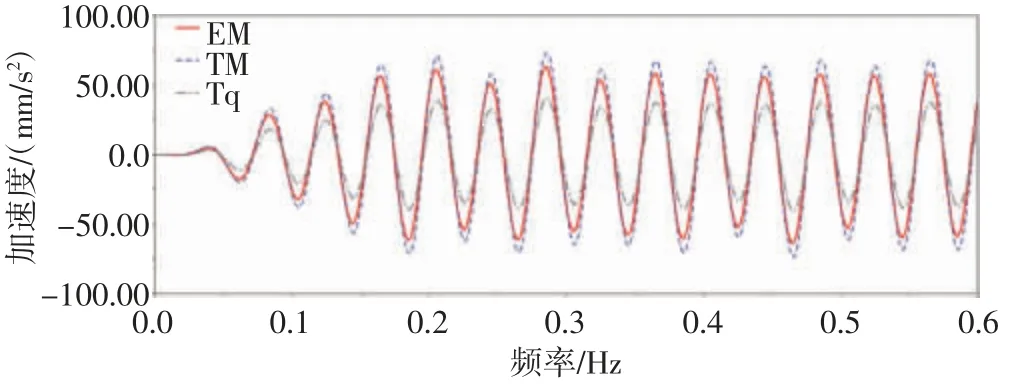
图8 悬后振动峰值时域曲线

图9 悬后振动峰值频域曲线

由于发动机怠速激励频率为25 Hz，可以看到经过FFT 变换后，都在25 Hz 处出现了振动峰值，这也验证了驱动频率的正确性。表5 和表6 示出隔振、悬后振动仿真与测试值对比。

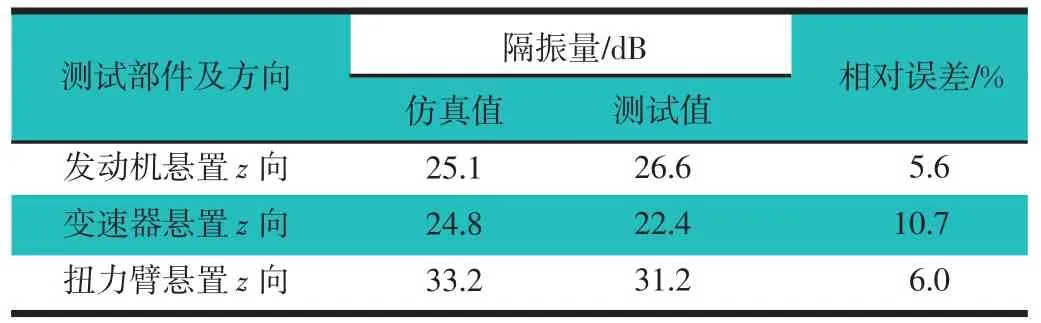
表5 隔振量仿真与测试对比

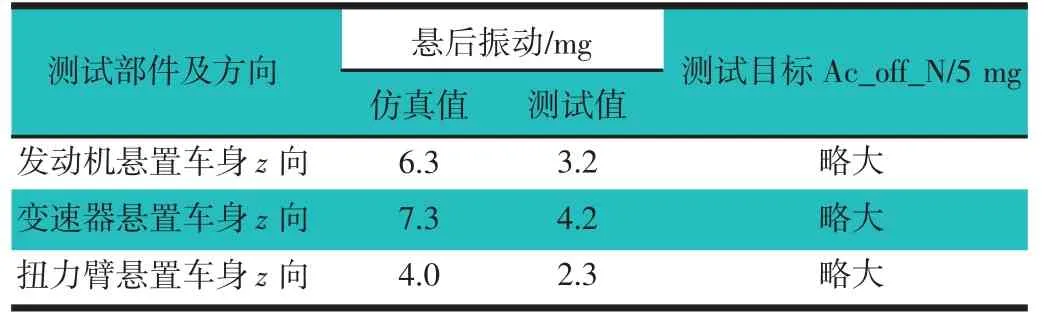
表6 悬后振动仿真与测试对比

表6 中，测试中更多用mg 来评价悬后振动。其中10 mm/s2等于1 mg。通过对比可以看到，无论是隔振还是悬后振动，都会出现一定偏差，这是因为：首先，文章基于发动机理想状态建立了驱动函数，其中的气体扭矩等指标皆为近似算法，而且忽略了活塞与气缸摩擦等很多影响因素；其次，隔振与悬后振动与车身安装点动刚度密切相关，需要车身柔性化才能近似逼近真实值，文章建模基于刚体车身建模，综上有略微偏差是可以接受的。

4 结论

针对发动机怠速对整车振动的影响，通过建立整车动力学模型与发动机激励驱动，利用仿真分析方法探讨了悬置振动特性，具体研究结果表明：

1）基于整车多自由度建模，能够将悬架硬点及弹簧减振等因素考虑进去，完善传递路径，更贴近实车状态。

2）通过整车模态对比分析，能够进一步优化验证初始设计参数，实车将整车纵向与垂向耦合频率优化到间隔1 Hz，规避了实车耦合问题。

3）悬置隔振量仿真大于20 dB；悬后振动小于8 mg，符合目标要求。总体看该评价与实车近似，再次论证了该方法的可行性与新颖性。