不同插值方法对近地面风速插值的精度对比分析

黄鹏飞 常怡婷 赵甲林

（1.63850部队 白城 137001）（2.国家海洋技术中心 天津 300112）

1 引言

近地面层是大气边界层中稳定存在的，最接近下垫面的部分，高度通常在100m以下，它的湍流活动剧烈且以机械湍流为主。近地面风靠近地面，在运动过程中由于连续不断地受地表组成物质和地表障碍物的作用，从而形成了与高空大气运动不同的特性，具有明显的紊流性质、具有较大的风速铅直速度。而近地面层又是人类生活的主要区域，长时间连续观测和研究近地面风速具有重要价值。

气象数据的连续性是数据应用的基础，近地面风速数据往往会因为观测设备的各种原因造成或多或少的缺失，如何对缺失数据进行更加准确的插补是一项重要工作。常用的插值方法包括：线性插值、最近邻点插值、自然邻点插值、三次多项式插值、反距离权重插值、克里金插值等，不同的插值方法在近地面风速数据插值的应用效果有比较大的差异，如何选择拟合效果更好的插值方法是研究的重点[1～10]。谢建华等通过建立不同高度风速相关性方程来对缺失层数据进行估算，认为非线性分析得出的修正数据更加接近实际情况[11]。韩二红等把气象再分析资料应用近地面风速数据的插补中，并对不同插值方法进行了对比分析[12]。

本文分别采用线性插值、三次样条插值、反距离权重法对近地面风速数据进行插值分析，通过设定检测点的方式，对不同方法所得插值数据与实测数据进行比较，并分析了不同插值方法的插值精度。

2 插值方法原理

2.1 线性插值

线性插值是指插值函数为一次多项式的插值方式，其在插值节点上的误差为零，具有简单方便的特点，原理如下。

假设函数y=f(x)在两点x0，x1上的值分别为y0，y1，求多项式：

以上插值多项式为一次多项式，这种插值称为线性插值。

2.2 三次样条插值法

样条插值是用平滑曲线来对各主干点进行拟合的方法，通过构造多项式来形成一条把所有主干点连接起来的平滑曲线，三次样条插值函数一般比较常用，原理如下。

给定区间[a，b]的一个划分：a=x0＜x1＜x2＜…＜xn=b和区间[a，b]上的一个函数f(x)，若函数S(x)满足下列条件：

1）一致通过n+1个插值点(xi，yi) ；

2）二阶连续，即S(x)∈C2[a，b]；

3）三次分段，即在每一个小区间[xi-1，xi](i=1，2…n)上均为三次多项式。

则称S(x)是函数f(x)的三次插值样条函数，比较常用的样条函数为Spline和Cubic。

2.3 反距离权重法

反距离权重法，即IDW（Inverse Distance Weight），是一种以插值点与观测已知点之间距离为权重的插值方法，可以以确切的或者圆滑的方式插值。幂指数控制着权系数如何随着离开一个格网结点距离的增加而下降。

数学表达式为

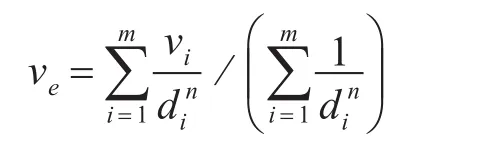
其中，ve为插值点的估算值，vi是第i个已知点的变量值，di是第i个已知点与插值点之间的距离；m为参与计算的已知点个数；n为幂指数，它控制着权重系数随插值点与样本点之间距离的增加而下降的程度。

反距离权重法主要用于三维空间插值，本文将其简化后用于二维线性插值。

3 数据处理与验证

为了对上述几种插值方法的插值效果进行比较，在建模前预留检测点，通过计算实测数据与插值数据的误差来评估各种方法的优劣。为了兼顾定量和定性评估，采用平均绝对误差法（MAE）和平均相对误差法（MRE）。MAE反映估计值的实测误差范围，定量给出误差值；MRE反映不同数据量或不同要素误差相对值，定性给出误差范围。MAE和MRE的表达式如下：

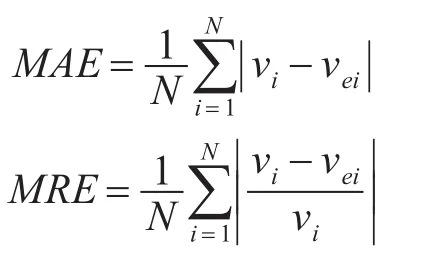
其中，vi为实测值，vei为估算值。

本文随机选取了100组近地面实时风速测量数据和100组近地面日平均风速测量数据，每组分别包含3.5m、10m、20m、34m、55m、75m、101m等7层风速数据，分别采用线性插值、三次样条插值（分别使用Spline和Cubic样条函数）、简化后的反距离权重法进行插值分析，分别将10m、20m、34m、55m、75m层作为检测点，计算预设的不同检测点的平均绝对误差和平均相对误差。

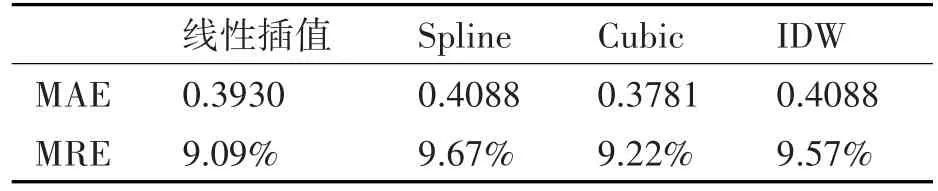
表1 10m层瞬时风速插值分析

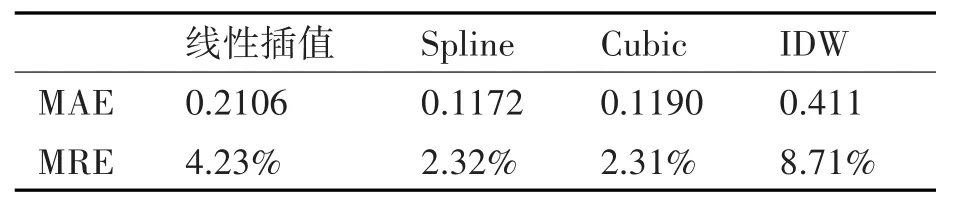
表2 10m层平均风速插值分析

表3 20m层瞬时风速插值分析

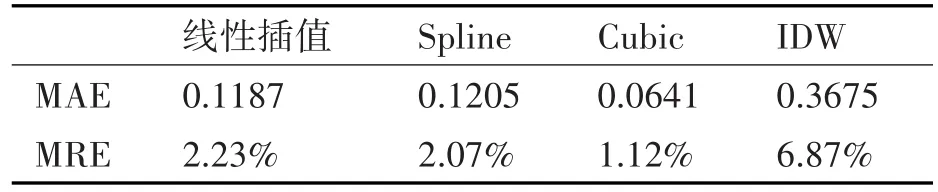
表4 20m层平均风速插值分析

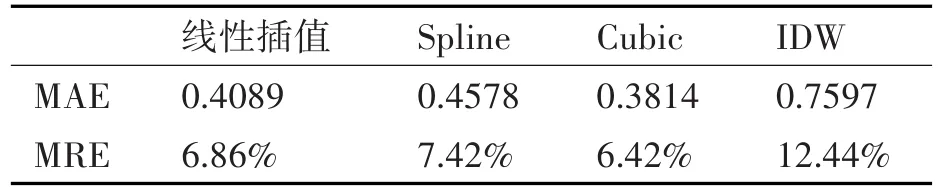
表5 34m层瞬时风速插值分析

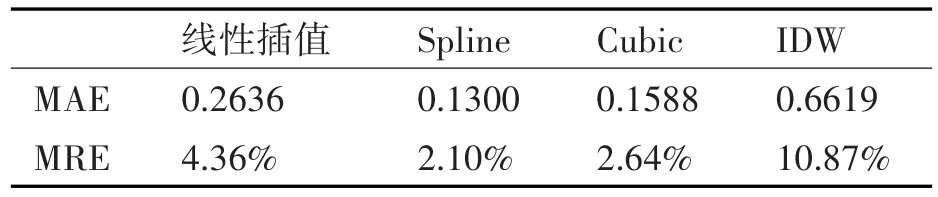
表6 34m层平均风速插值分析

表7 55m层瞬时风速插值分析

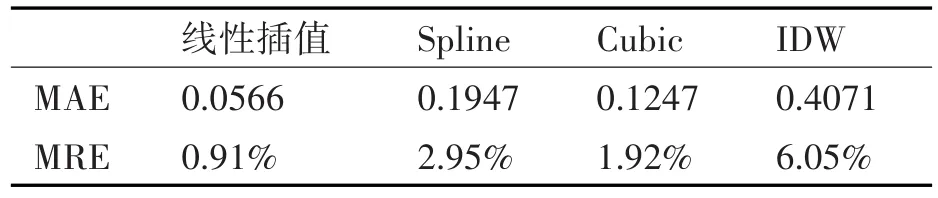
表8 55m层平均风速插值分析

表9 75m层瞬时风速插值分析

表10 75m层平均风速插值分析

表1～10分别计算了10m、20m、34m、55m、75m层检测点实测数据和不同插值方法所得估计值之间的平均绝对误差（MAE）和平均相对误差（MRE）。

对比每层检测点的插值分析数据可以看出，对于同一种插值方法而言，日平均风速的插值效果要明显优于瞬时风速的插值效果。此种现象的产生是由于瞬时风速受小尺度湍流影响较大，风速随着高度变化的随机性较强，使得瞬时风速的插值效果相比于平均风速的插值而言要差一些。风速的日平均数据由于消除了瞬时小尺度湍流的影响，其平滑性和规律性更好，相应的插值效果也更好。

图1 瞬时风速插值精度对比

图2 平均风速插值精度对比

图1和图2分别表示不同插值方法对瞬时风速和平均风速进行插值后的平均相对误差。

从图1可以看出，对于瞬时风速而言，采用线性插值方法和使用Cubic插值函数的三次样条插值方法所得插值数据的精度要明显优于采用Spline插值函数的三次样条插值法和反距离权重法。从图2可以看出，对于日平均风速而言，采用Cubic插值函数的三次样条插值方法所得结果是最好的，线性插值和使用Spline插值函数的三次样条法虽然稍逊于采用Cubic插值函数的三次样条插值方法，但是其精度依然很高，平均相对误差在3%左右，仍然能满足数据使用要求。反距离权重法所得插值结果则较差，与其余三种方法所得数据精度差距较大。综上所述，无论是瞬时风速还是日平均风速，采用Cubic插值函数的三次样条插值法对近地面风速进行插值，效果最好。

4 结语

本文以近地面瞬时风速和日平均风速数据为基础，研究不同插值方法在近地面风速插值的精度分析，结论如下：

1）受到小尺度湍流的影响，瞬时风速数据的插值精度要明显劣于对日平均风速的插值精度；

2）对于近地面瞬时风速而言，采用线性插值方法和使用Cubic插值函数的三次样条插值方法所得插值数据的精度更好；

3）对于近地面日平均风速而言，采用Cubic插值函数的三次样条插值方法所得结果最好，反距离权重法则最差。