SIFT和 SURF算法在偏振图像匹配中的应用研究*
2020-12-02
(中国人民解放军陆军炮兵防空兵学院 合肥 230031)
1 引言
图像匹配是偏振图像处理领域的一项重要技术,在计算机视觉、偏振图像分析等领域有广泛的应用。在研究偏振光成像技术时,为了获取目标的偏振信息(如偏振度、偏振角等),必须对偏振成像系统获得的多幅不同偏振方向图像进行数理运算。由此,图像配准对于偏振成像系统非常重要。David G.Lowe[1~2]提出的 SIFT 算法和 Herbert Bay[3~4]等提出的SURF算法是尺度不变特征的提取算法的代表。陈敏[5]等在低空无人机影像的配准上做过对比研究,秦枭[6]等在岩体露头面点云获取中做过比较分析,徐妍[7]等在无人机影像配准中做过比较,齐冰洁[8]等高分辨率遥感图像匹配中做过一些工作,但是在偏振图像处理应用中,尚缺少有实际意义的成果。本文基于实验室定焦分孔径同时式偏振光成像系统的偏振图像进行特征点提取和图像匹配实验,结合实验结果比较两种算法的性能。
2 偏振图像配准需求分析
偏振图像解析后才能揭示偏振特性,然而解析需要获取的原始偏振图像在空间位置上严格一致,所以偏振图像配准必须在解析前完成。在实际的采集偏振图像过程中,采集图像的距离、角度、不同的温湿度、时间、物体所处的物理状态等不同,尽管采集偏振图像系统有好几种,但是获取的偏振图像均会有平移、缩放、旋转等缺陷,由于偏振图像的合成需要以点为单位进行,如果直接使用这些有畸变的偏振图像进行解析,那么偏振图像在几何上就不能对齐,所以就不能得到准确的指定目标的偏振信息。所以,这种偏振光成像探测系统的采集的各个方向之间误差必须消除,所以必须对偏振图像进行配准。
3 SIFT算法
1999年,David Lowe提出SIFT算法,是具有尺度不变性的典型的局部特征描述子,后来David Lowe在2004年将其整理完善。SIFT算法主要分为三步:特征点提取;生成特征描述子;特征点匹配[11]。
3.1 特征点提取
1)尺度空间的极值检测使用高斯模糊来构建尺度空间,尺度变换的唯一变换核是高斯卷积核,并且是唯一的线性核。
2)定位特征点
定位特征点主要有两个任务,一是去除低对比度的特征点,二是去除不稳定的边缘响应点。拟合精细函数来提取关键点的位置和尺度,去掉不稳定的点,由高斯差分运算造成的边缘响应干扰用Hessian矩阵除去,达到优化特征点检测结果的目的[10]。
3)分配特征点的主方向
为了实现图像旋转不变性,需要对特征点指定参数方向。选择一个固定尺度的高斯平滑图像,然后通过计算特征点处的两个值,一是梯度大小,二是角度。再将刚才计算出来的特征点建立角度直方图,局部梯度的主方向可以从峰值来看出[12]。
3.2 生成特殊描述子
以特征点为中心取一个区域,并对其中点的梯度做高斯加权。假设采用16像素×16像素的像素矩阵,周围区域被分割为若干子区域,其中每个子区域大小为4像素×4像素,并且在刚才分割的每个子区域中绘制梯度直方图,则描述子的维数就是4×4×8=128维,该特征向量就是SIFT描述子。
3.3 特征点匹配
特征点的相似性判定度量用euclidean metric来表示,设定某个阈值,我们要求最近邻距离与次近邻距离比值小于这个设定值,就认为特征匹配成功[13]。
哦,事情是这样的,团长说,最近我听到反应,你和砖子闹了点小矛盾,影响别人生活了。赵仙童笑笑,说我和砖子很恩爱,怎么可能闹矛盾影响别人的生活?我想一定是有人造谣,团长,你是代表党跟我谈话的,请你一定要相信群众,特别是我们这些还算得上有点名气、有点身份的群众,决不允许任何无是生非的人泼污水,那是不利于团结、不利于构建和谐社会、不利于社会主义精神文明建设的。
4 SURF算法
SURF算法是基于SIFT算法的改进,计算复杂度更低、耗时更短,且具有高鲁棒性,改进了关键点的提取方法和描述方式,比SIFT更为高效。SURF特征匹配算法以下步骤:特征点检测、构建特征描述子和特征点匹配[14]。
4.1 特征点检测
4.1.1 构建Hessian(黑塞矩阵)
经过高斯滤波后的Hessian矩阵定义为
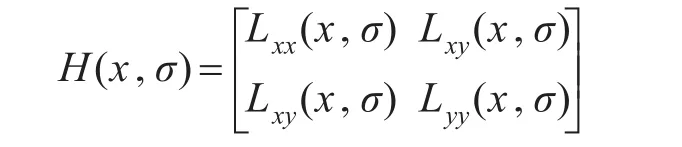
判断Hessian矩阵的判别式的局部极大值,将其对应的点作为关键点。高斯差分运算造成的边缘响应干扰用Hessian矩阵除去,达到优化特征点检测结果的目的[10]。
4.1.2 构建尺度空间
SURF算法的尺度空间由O组L成组成,且高斯模糊系数逐渐增大。SURF算法中,各个octave层之间的待检测图片尺寸大小是相同的,只改变了滤波器的大小[15]。
4.1.3 特征点定位
4.1.4 特征点主方向分配
在特征点区域内,以60°区域为单位,统计其haar小波特征,统计所在区域内所有特征点的水平和垂直哈而小波特征总和,然后再以相同大小区域旋转,旋转一周后以小波特征最大的扇形方向作为该特征点的主方向[15]。
4.2 构建特征描述算子
我们需要在关键特征点的主方向四周取一个矩形区域块,大小为4×4。并在每个区域中统计25个像素的haar小波特征。分别为水平方向和垂直方向,都是相对于主方向而言。haar小波特征分别为水平方向、垂直方向绝对值之和,水平以及垂直方向值之和。
4.3 特征点匹配
特征点匹配利用特征描述子之间的euclidean metric作为特征点的相似性判定度量,如果最近邻距离与次近邻距离比值小于某个阈值,则认为匹配成功。SURF算子中,计算两个特征点间的欧式距离和Hessian矩阵迹的判断。两个特征点的匹配度越好即通过欧氏距离越短来判定。
5 实验与数据分析
实验平台为CPU为Inter(R)Core(TM)i7-3770k 3.50GHz,内存 16G的 LG-PC,以 Matlab实现基于SIFT和SURF的偏振图像匹配,最后再分析SIFT和SURF算法在偏振图像匹配效果。实验结果如图1、图2、图3、图4所示。

图1 模板图与实时图

图2 模板图与实时图匹配效果

图3 模板图与实时图

图4 模板图与实时图匹配效果
表1为实验数据表,用于偏振图像匹配实验数据。

表1 偏振实验图像匹配数据记录表
实验结果表明,基于SURF的图像匹配算法在偏振图像特征点数量上明显优于基于SIFT的图像匹配算法,但是SIFT算法复杂度较高,虽匹配精度高于SURF算法,但是运行效率相比太低。
6 结语
通过对基于SIFT和SURF两种图像匹配方法进行了匹配实验研究,对比两种算法在多路平行同时偏振光成像系统数据所得匹配特征点数量和两种算法在实验平台上运行时间。根据实验所得结果分析评价了两种算法的精度、匹配速度。相对来说,基于SURF的图像匹配算法在偏振图像特征点匹配速度上明显优于基于SIFT的图像匹配算法,若考虑到偏振光成像系统应用的实时解析问题,采用SURF算法更适合。SIFT算法复杂度较高,虽匹配精度高于SURF算法,但是运行效率相比太低,更适合用于离线解析这类对精度要求高场景中。
