聚醚酰亚胺长杆弹弹托在膛压载荷下的动力学响应
2020-12-01张庆明巨圆圆陆阳予
乔 宇,陈 利,张庆明,巨圆圆,陆阳予
(1. 北京理工大学爆炸科学与技术国家重点实验室,北京 100081;2. 海军研究院,北京 100161)
长杆弹是目前军事装备中最常用的一种弹体,主要依靠自身强大的动能来穿透目标[1-2]。长杆弹的弹托属于消极质量,通常采用低密度、高强度的复合材料制成,因而可以大大减轻弹丸的总质量,减少消极动能损耗,从而提高弹丸出炮速度,提升穿甲威力[3-5]。
国内外学者在复合材料弹托的发射强度及结构优化方面已开展了很多研究工作。佟文敏等[6]应用GV-NIKE2D 程序对长杆弹配用复合材料弹托的不同结构进行了发射强度计算,对影响弹托发射强度的结构因素,如尾椎套的有无及其厚度、材料进行了分析和比较。Burns 等[7]开发了LAMPAT 软件,研究了石墨纤维增强环氧树脂复合材料弹托的结构及材料缺陷对发射强度的影响,提出了一种新的破坏准则,同时结合试验确定了强度极限。唐蜜等[8]对短纤维复合材料弹托的发射过程进行了数值模拟,将间隙啮合技术应用于弹托上,通过间隙调整使得弹托危险齿根面的等效应力值比传统啮合方式减小29%以上,且各齿根面的应力趋于接近。刘世国[9]以125 mm 国产碳纤维/环氧树脂复合材料弹托为研究对象,采用3D 壳单元建立了复合材料分层模型,研究了弹托存在的强度问题,给出了优化方案。闫季华[10]针对短切碳纤维增强尼龙弹托,设计了啮合齿和尾椎结构,改进了注塑工艺,经射击试验验证,着靶姿态正确,满足发射强度要求。Wang 等[11]针对某穿甲弹玻纤层压复合材料弹托,应用ABAQUS 软件对弹丸发射强度进行数值研究,分析了材料层缺失对弹托应力分布的影响。
随着科学技术的发展,弹托材料也在不断更新换代,目前国内外研究的纤维增强复合材料弹托主要采用环氧树脂、聚碳酸酯等作为基体材料,而对采用聚醚酰亚胺作为纤维增强复合材料弹托基体材料的研究较少。聚醚酰亚胺是一种新型的热塑性塑料,与其他热塑性基体材料相比,具有更高的强度、耐热性和稳定性,如聚碳酸酯的弹性模量和屈服应力分别为2.45 GPa 和65 MPa,冲击强度为108 kJ/m2,热变形温度为135 ℃,而聚醚酰亚胺的弹性模量为3.3 GPa,屈服强度可达103 MPa,冲击强度为140 kJ/m2,热变形温度在198~208 ℃之间,相比之下聚醚酰亚胺在各方面均表现出明显优势。
本研究中的平头长杆弹是一种由二级轻气炮发射的超高速动能弹,用于研究动能弹对混凝土靶、钢靶的侵彻效应。在现有发射条件下,长杆弹初速可达2 700 m/s 左右。为了研究更高速(3 000 m/s 以上)动能弹的毁伤效应,需要通过改进弹托结构来提高弹丸初速。本研究利用LS-DYNA 有限元软件,采用短玻璃纤维增强的聚醚酰亚胺复合材料作为长杆弹弹托和闭气环的材料,对长杆弹在膛压载荷作用下的动态响应过程进行数值模拟,并依据计算结果对弹托结构进行改进优化,减轻弹托质量,以达到提高长杆弹初速的目的,以期为弹托的结构设计提供参考。
1 动力学模型
1.1 计算模型
长杆弹结构包括弹芯、弹托及闭气环3 部分,且各构件同轴,均为几何对称结构,如图1 所示。弹托结构是基于常规火炮发射的穿甲弹弹托设计而成,为便于加工,去掉弹带、尾翼、密封套等结构,采用简单的三等分瓣型弹托,弹托外径与轻气炮口径一致,三瓣弹托与弹芯通过环形齿啮合在一起。梯形或三角形环形齿具有良好的轴向传递推力性能,其啮合面通常设计成垂面或带有小斜度(2°左右)的斜面,已有的实验研究证明,等质量杆弹采用凸台式环形齿结构比采用凹槽式结构具有更低的极限穿透速度[1,12],因此长杆弹采用凸台式三角形齿结构,啮合面垂直于弹轴,啮合方式采用等距间隙啮合。此外,在弹托尾部增加相同材料的闭气环,以防止弹底高压气体泄漏。闭气环是一个完整的环形结构,与弹芯之间没有啮合。弹托头部的凹槽形状是为了弹托出炮后在空气阻力作用下能顺利分离、脱落。
利用 LS-DYNA 软件建立有限元计算模型,如图2 所示。长杆弹在膛内发射过程中的受力状态非常复杂,由于计算过程仅限于弹丸直膛加速阶段,因此根据其结构特点和发射环境,对计算模型作出如下基本假设[13-14]:(1)载荷轴对称,弹底气体推力的合力与炮膛轴线、弹丸轴线一致;(2)同一时刻,弹底压力对弹丸承载面的作用力处处相同,弹托卡瓣之间、弹托与弹芯之间无高压气体渗透;(3)不考虑弹丸膛内径向振动、头部气动阻力以及离心力的影响。有限元计算模型采用拉格朗日实体进行网格划分,对应力幅值和应力梯度较大处,如环形齿、圆角处,网格划分得密一些,以提高计算精度。
弹丸在膛内发射过程中,膛压载荷作用在闭气环底面,方向与底面法向一致,压力曲线见图3。由于弹丸在发射过程中受到炮管的约束作用,对弹托和闭气环与炮膛接触面上的所有节点设置UY 和UZ 约束。弹芯、弹托及闭气环之间均采用面面自动接触,接触面与目标面的选择是任意的。
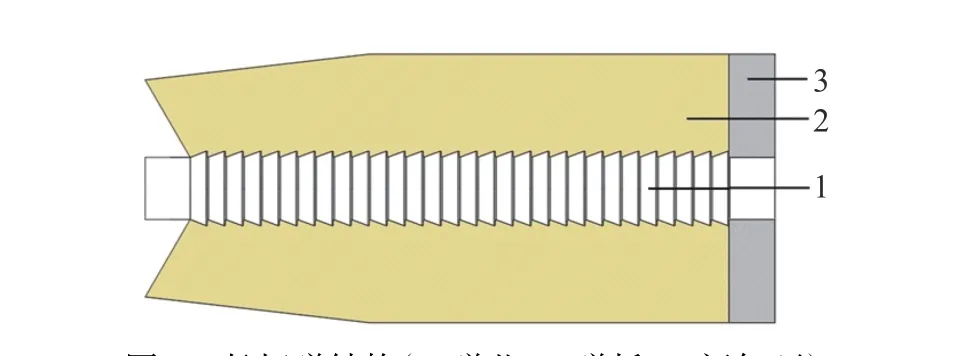
图1 长杆弹结构(1. 弹芯;2. 弹托;3. 闭气环)Fig. 1 Structure of the long rod projectile(1. Penetrator;2. Sabot;3. Obturator ring.)
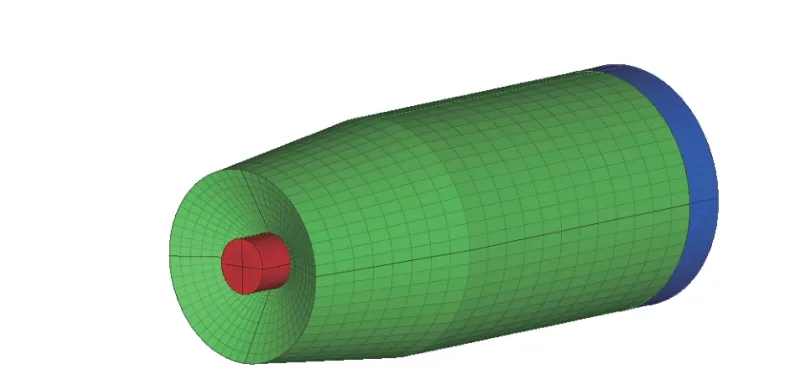
图2 长杆弹计算模型Fig. 2 Calculation model of the long rod projectile
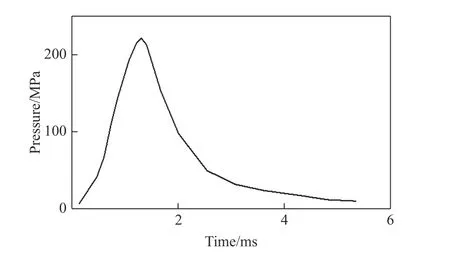
图3 膛压曲线Fig. 3 Bore pressure curve
1.2 材料模型及参数
弹芯材料为40CrNiMo 合金钢,采用调制热处理(淬火加高温回火)以改善其力学性能。弹托与闭气环均采用短玻璃纤维增强的聚醚酰亚胺复合材料(PEI GF30),短玻璃纤维在基体中均匀分布且取向随机,因此该复合材料可视为各向同性的塑性材料[15]。弹芯、弹托及闭气环均采用各向同性随动硬化塑性模型MAT_PLASTIC_KINEMATIC进行模拟,相关参数如表1 所示,其中: ρ0为材料密度,Ep为弹性模量, μ为泊松比,Y为屈服强度, εeff为等效失效应变。计算中,当单元或节点的即时等效应变超过材料本身的等效失效应变时,删除此单元或节点。

表1 塑性随动硬化模型材料参数Table 1 Material parameters in plastic-kinematic strength model
1.3 模型验证
使用30 mm 口径的二级轻气炮对该长杆弹进行发射试验,弹丸总质量87 g,炮管发射区段长10 m,利用磁测速技术测得弹丸的出炮速度为2 688.0 m/s。应用建立的长杆弹有限元计算模型对膛内发射过程进行仿真,试验所用的弹托、弹芯及建立的有限元几何模型如图4 所示。模拟弹丸的速度曲线和轴向位移曲线分别如图5、图6所示。1.3 ms 时轴向加速度达到最大值1.73 ×106m/s2,此时为膛内压力最大时刻,弹丸最终速度为2 756.2 m/s,比试验值大2.53%,轴向位移10.56 m,比实际发射炮管长5.63%,计算值偏大的原因在于忽略了弹丸与炮膛间的摩擦力及空气阻力。计算与试验结果吻合较好,验证了模型的有效性。

图4 长杆弹及有限元几何模型Fig. 4 Long rod projectile and finite element geometric model
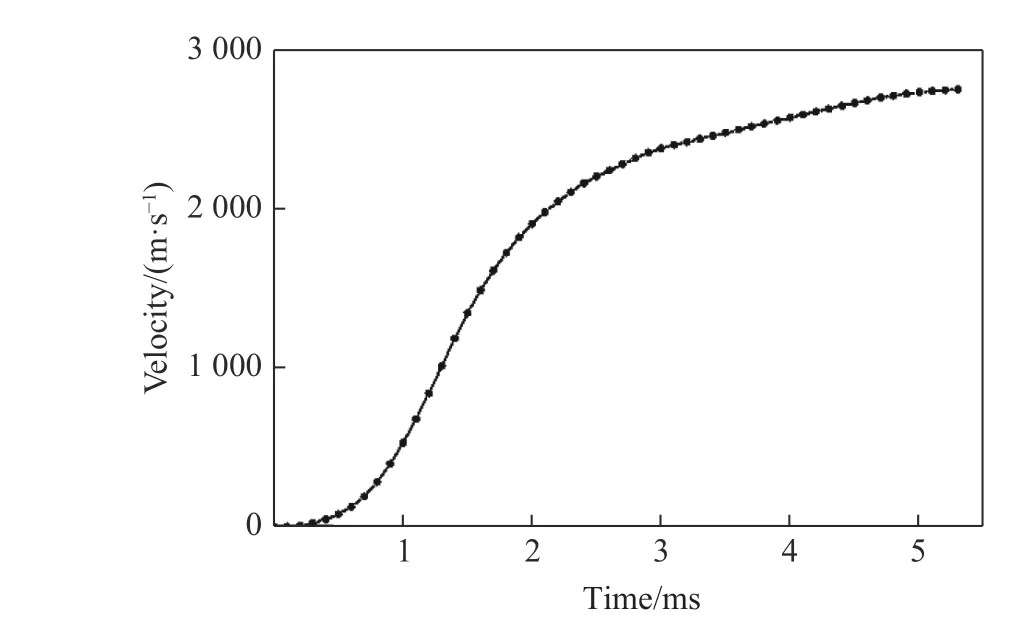
图5 弹丸速度曲线Fig. 5 Projectile velocity curve
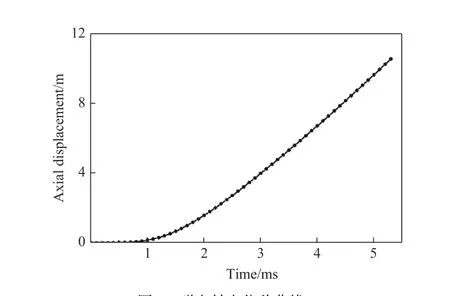
图6 弹丸轴向位移曲线Fig. 6 Axial displacement curve of projectile
2 膛压载荷下弹托的动态响应规律
对长杆弹在轻气炮膛压载荷作用下的动态过程进行数值模拟,为便于查看,取弹托1/4 模型进行分析,弹托在不同时刻的等效应力云图反映了弹托上应力分布随时间的变化规律,如图7 所示。由图7可以看出:初始受压时,弹托后齿应力首先开始增大,随着膛压迅速升高,压力由弹托尾部向头部传递,除后齿外,尾部的外围也承受了较大压力;1.3 ms 时,膛压升至最高,弹托各处应力基本都达到最大值,此时应力分布呈阶梯状,应力大小由尾部至头部递减,高应力区主要分布在弹托尾部外围附近及后齿上,最大应力值为490.3 MPa,出现在最后一齿的齿根处;1.3 ms 后,弹托各处应力随膛压的降低开始逐渐减小,尾部应力减小速率较缓慢,尤其是底面内径处,出炮时应力仍有300 MPa 左右。
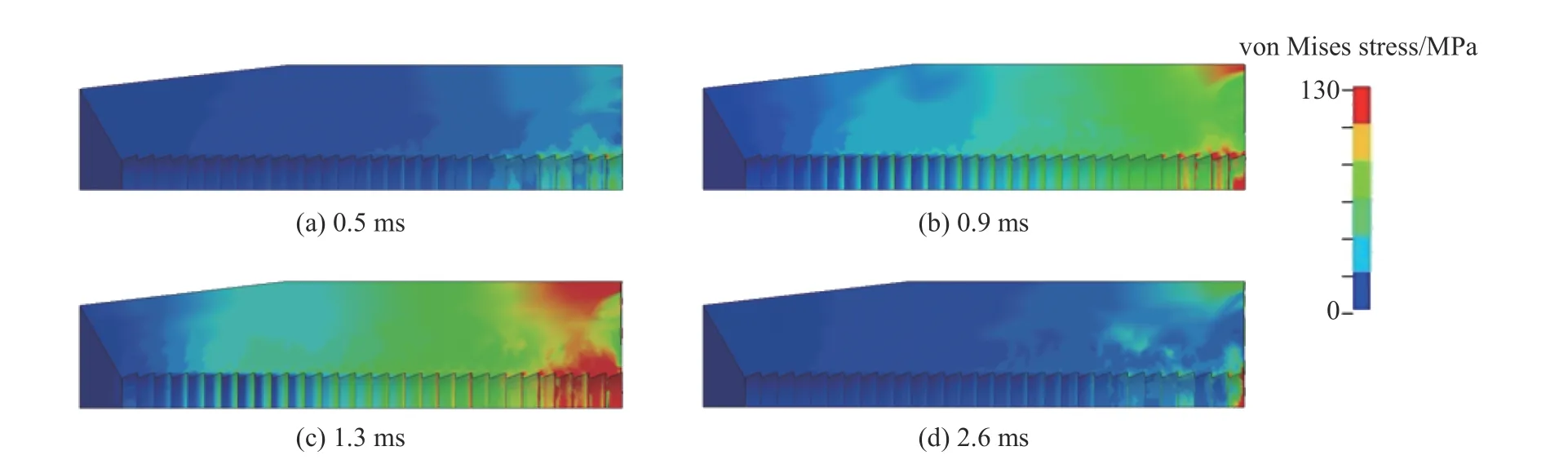
图7 不同时刻弹托的等效应力云图Fig. 7 Equivalent stress nephogram of the sabot at different moments
对弹托的环形齿进行编号,从头部到尾部依次为1、2、3、……、29 齿。在最大膛压时刻,弹托前齿与后齿的应力大小不同,同一齿上齿根与齿顶的应力大小也不同,1.3 ms 时各环形齿齿根和齿顶等效应力沿轴向的分布如图8 所示。由图8可以看出,无论是齿根还是齿顶,应力幅值由弹托后齿至前齿呈降低趋势,其中后齿齿根的应力变化幅度较大。同一齿上齿根应力大于齿顶应力,弹托最后6 齿的齿根与齿顶应力差值较大,29 齿应力差值达371.2 MPa。前8 齿齿顶应力非常小,仅有5 MPa 左右。在膛压载荷作用下,弹托前齿作用非常小,给弹芯传递压力更多地依赖于后齿,尤其是后齿齿根,整个发射过程中仅有28、29 齿齿根发生塑性变形,塑性应变分别为0.028、0.106,均未超过材料的失效应变,因此弹托满足发射强度要求。
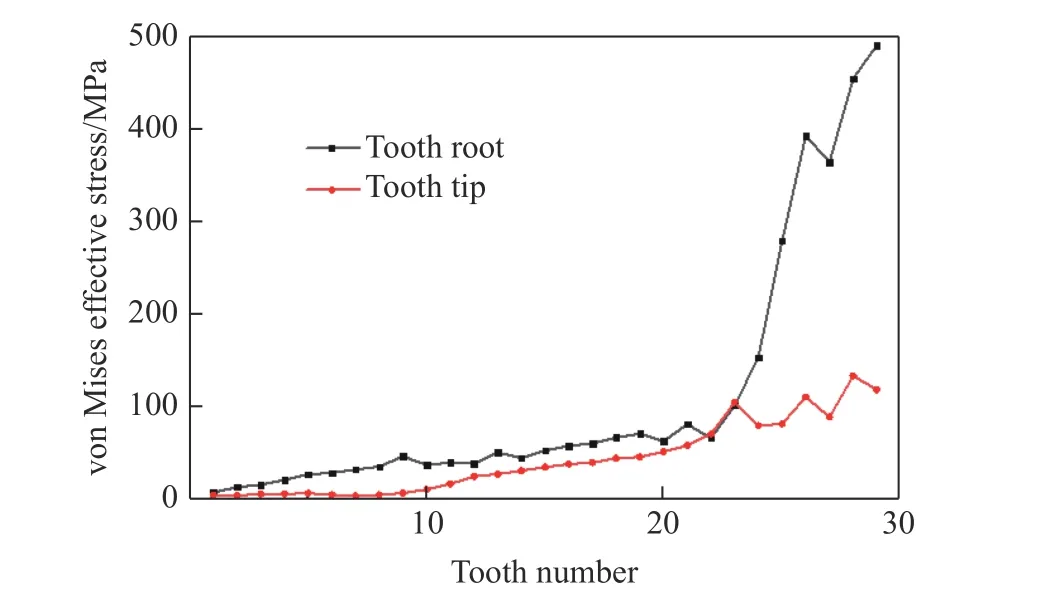
图8 最大膛压时刻弹托齿根和齿顶的等效应力Fig. 8 Von Mises effective stress of the tooth root and tip of the sabot at the time of maximum bore pressure

图9 不同时刻闭气环的等效应力云图Fig. 9 Equivalent stress nephogram of the obturator ring at different moments
复合材料闭气环在传递压力给弹托的过程中,与弹托接触的面(A-A 面)及底面(B-B 面)在不同时刻的等效应力云图如图9 所示。由图9 可以看出,接触面的内径处为主要受力部位,在膛压变化过程中,一直处于高应力状态,这是由于内径与弹芯的最后一齿直接接触,在推动弹丸运动时直接传递压力给弹芯,因而受到弹芯的反作用力较大,并且在压力载荷降低时,仍然保持较高的应力。随着膛压的升高,除内径外,接触面外径处也产生了较高的应力;1.3 ms 后,膛压开始降低,该处应力也开始减小,但减小速率相对较慢。闭气环底面在不同时刻的应力值均为内径处较大,外径处较小,在最大膛压时刻,底面内径处比接触面内径处的高应力区范围大。
总体来看,闭气环接触面比底面更早出现应力高点,且在同一时刻,接触面高应力分布面积更大;接触面的内径和外径处均发生了塑性变形,而底面各处没有塑性变形。
3 弹托结构改进
基于上述的仿真结果和对弹托结构的技术分析,以降低弹托质量、提高长杆弹初速为目的,对弹托结构进行改进。在发射过程中,弹托的头部及前齿受力非常小,强度裕度较大,因此在保证弹芯稳定性的前提下,适当削掉弹托头部,以减小弹托质量,并且为了有利于弹托出炮后脱落,保留弹托头部的迎风槽形状。改进的弹托结构如图10所示。
对改进后的复合材料弹托在膛压载荷下的动态过程进行数值模拟。两种弹托结构在最大膛压时刻的等效应力云图如图11 所示。对比图11(a)和图11(b)发现,高应力区仍集中在弹托尾部,但改进结构的材料利用率相对较高,低应力区占比较少。弹托的塑性变形位于最后3 齿的齿根上,塑性应变分别为0.003、0.037 和0.110,均未超过材料的失效应变,满足发射强度要求。
两种弹托结构的长杆弹在膛内发射过程中的速度及轴向位移对比曲线分别如图12、图13 所示。改进结构的弹丸加速度始终大于原结构的弹丸加速度,最大膛压时刻左右加速度相差最大。在相同的发射技术条件下,改进后的长杆弹在4.9 ms时轴向位移即达到了实际发射炮管长度,此时弹丸速度为3 380.0 m/s,与原始结构相比,弹托质量减小了16 g,在满足发射强度的情况下,出炮速度提高612.2 m/s,达到3 000 m/s 以上的发射速度要求。
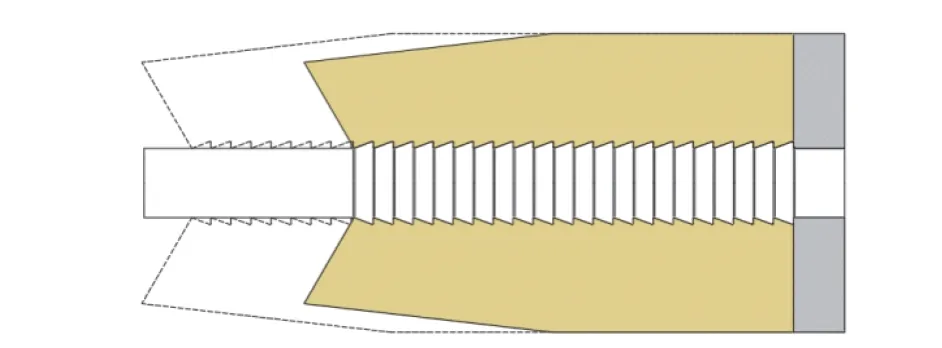
图10 改进的弹托结构Fig. 10 Improved sabot structure
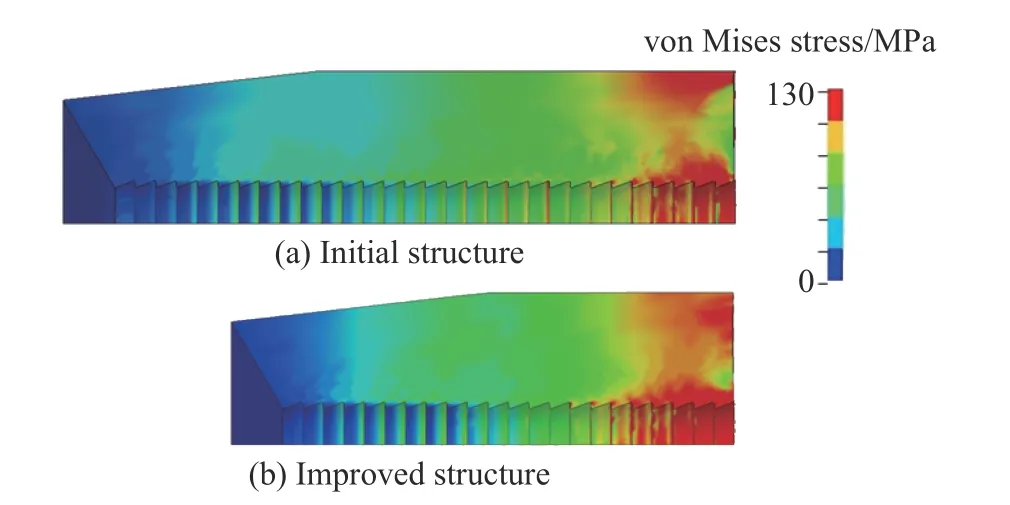
图11 两种结构的弹托在最大膛压时刻的等效应力云图Fig. 11 Equivalent stress nephograms of the two structures of the sabot at the time of maximum bore pressure
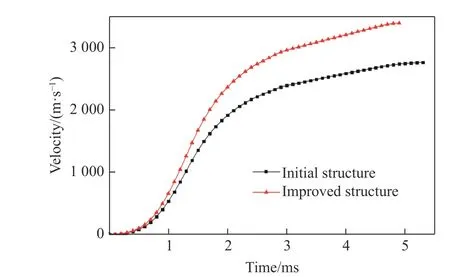
图12 两种结构弹丸的速度曲线Fig. 12 Projectile velocity curves of the two structures
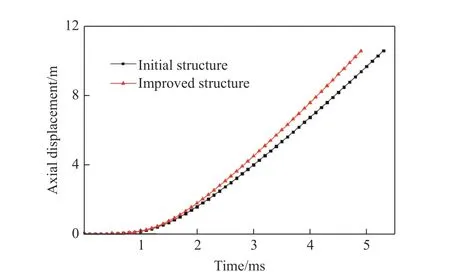
图13 两种结构弹丸的轴向位移曲线Fig. 13 Projectile axial displacement curves of the two structures
基于聚醚酰亚胺弹托在膛压载荷作用下的动态结构响应来改进弹托结构,将应力值较小的部位作了轻量化处理,达到了减轻弹托质量、提高长杆弹初速的目的。但改进后的弹托后齿应力仍相对较大,齿部结构及啮合方式均不是最优,另外,迎风槽也可以设计不同的结构。因此对于聚醚酰亚胺弹托结构的改进,还有待进一步研究。
4 结 论
通过建立长杆弹的动力学计算模型,对聚醚酰亚胺复合材料弹托在膛压载荷作用下的动态过程进行了数值模拟研究,得出以下主要结论。
(1)在膛压载荷作用过程中,弹托后齿是主要的受力部位,后齿齿根出现塑性变形,而头部及前齿受力较小。最大膛压时刻,弹托各处应力达到最大,高应力区主要分布在弹托尾部外围附近及后齿上;弹托齿根、齿顶应力大小不同,且与齿的位置有关。
(2)闭气环与弹托接触的面与底面的应力分布不同,接触面比底面更早出现应力高点,且在同一时刻,接触面高应力分布面积更大;塑性变形的位置主要集中在接触面的内径和外径附近。
(3)通过改进弹托结构,提高了弹托的材料利用率,并且在满足发射强度要求的前提下,弹托质量减轻了16 g,从而使弹丸初速提高了612.2 m/s,达到了3 000 m/s 以上的发射速度要求。
