基坑开挖与临近地铁隧道的相互影响

唐小雨，郝屹峰，范一丁，张毅磊

(苏州科技大学 土木工程学院，江苏 苏州 215011)

0 前 言

随着我国经济的发展，城镇化速度的加快，城市居民密度越来越大，地面上的交通已很难满足人们的需求，这就促使了地铁隧道的发展[1]。由于地铁的出现，地铁站周边的土地迅速增值，促进了以地铁站为中心的城市群发展起来，进而地铁隧道附近出现了许多大而深的基坑工程[2]，这对地铁的正常运营产生了许多不利影响，同时地铁持续运行产生的振动荷载给临近的基坑工程也带来了一些安全隐患[3-5]。因此，本文对临近苏州轨道交通1号线的汽车西站基坑工程进行有限元分析，通过监测结果与模拟结果的对比分析，深入探究基坑开挖与地铁隧道之间的相互作用，以期为以后的实际工程提供有价值的参考。

1 工程概况

江苏省苏州市汽车西站基坑开挖工程基坑近似矩形，基坑工程为地上2层，地下1～2层建筑，地下1层区东西向最长约340 m，南北最宽约90 m；地下2层区东西向最长约320 m，南北最宽约80 m。地下1层区基坑挖深为8.3 m，地下2层区基坑挖深为11.7 m。

基坑围护结构外边缘距离轨交1号线盾构区间最近约18.3 m。轨交1号线该区段盾构区间顶标高为-9.8 m，底标高为-16.8 m，直径为6.2 m。东侧东南角为已建轨交1号线苏州乐园站6号出入口，该出入口前期采用SMW工法桩+钢管内支撑围护，该基坑与轨道1号线剖面关系如图1所示。

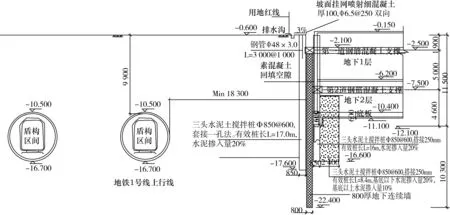
图1 基坑与轨道1号线剖面关系

2 数值模拟

2.1 建立有限元模型

对基坑与轨道交通1号线剖面进行二维有限元分析。以该实际工程为依托，建立二维有限元模型，基坑右侧围护结构与左侧对称，基坑长50 m，深11.7 m。根据圣维南原理，深基坑开挖的影响范围是其深度的3～5倍[6]，为简化计算模型，本文采用ABAQUS有限元分析软件建立了尺寸为150 m×40 m的二维模型，模型左右边界条件设置为约束x方向位移，下边界条件设置为约束x和y方向位移，最终有限元模型如图2所示。

图2 基坑与轨道1号线有限元模型

2.2 计算参数的选取

根据实际工程的地勘报告，该基坑工程共有7层土体，各土层力学参数如表1所示。地下连续墙、搅拌桩以及隧道衬砌均为混凝土结构，在开挖过程中视为弹性材料，弹性模量为30 GPa，泊松比为0.3，密度为2 500 kg/m3。

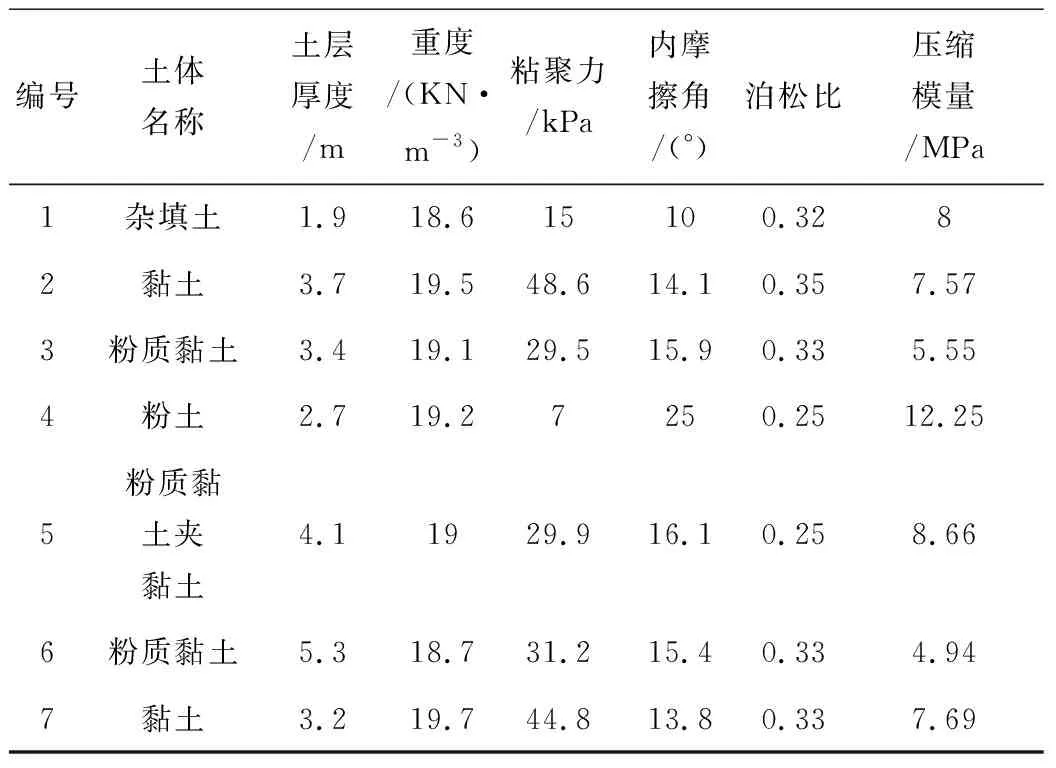
表1 各土层力学参数

3 监测结果与模拟结果对比

3.1 地下连续墙水平位移的对比

根据实际基坑工程开挖步骤，选取3个关键工况的监测数据和模拟数据进行对比分析，分别为：①开挖第1层土地和设第1道支撑；②开挖第2层土体和设第2道支撑；③开挖至基坑底部。图3～4分别表示地连墙水平位移在不同工况时监测数据和模拟数据的变化情况。

图3 监测数据

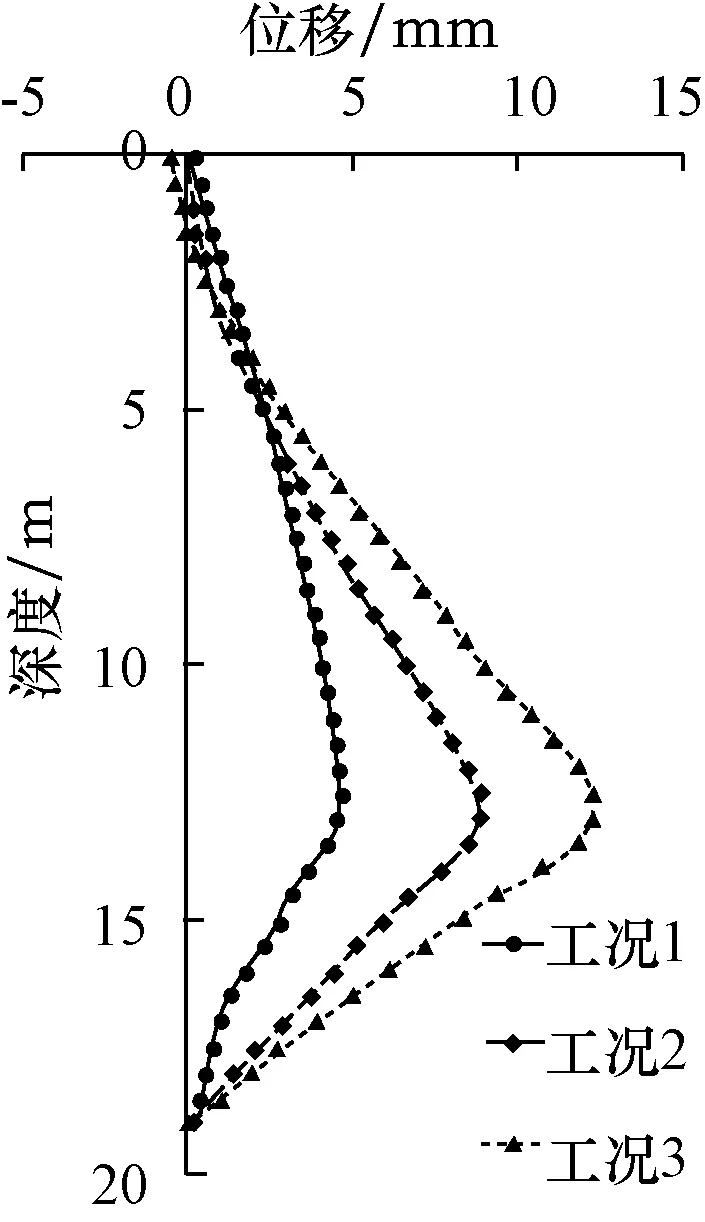
图4 模拟数据

从图3～4中可以看出，随着开挖深度的增加，地连墙的水平位移不断增加，且监测曲线和模拟曲线均表现为弓形，说明设置的两道支撑对地下连续墙的水平位移起到明显的抑制作用。对比两者曲线可以发现，在工况相同时，模拟所得的地连墙最大水平位移均大于监测值，且开挖结束后模拟所得的地连墙最大位移发生在深度约为13 m处，最大位移为12.21 mm，而监测值却在约10 m处，最大位移为9.73 mm，分析模拟地连墙产生最大位移区域下移的原因可能是由于在实际基坑工程中，围护结构右侧设置了长为8.4 m，直径为2.4 m的三头水泥土搅拌桩，这与地连墙、地墙两侧搅拌桩形成了刚度较大的围护结构，有效地限制了土体向坑内移动，而在模拟时，为简化模型，未考虑三头水泥土搅拌桩的影响，致使模拟的围护结构刚度小于实际围护结构刚度，最终使得模拟的地连墙产生最大位移的区域有所下移。在工况相同时，模拟数据均大于监测数据，这对实际基坑开挖工程具有一定的预测作用。

3.2 围护结构后地表沉降对比

对地表沉降的研究，本文选取地铁隧道侧的地表为研究对象。图5～6分别为围护结构后地表沉降的监测数据和模拟数据。从图5～6可以看出，监测与模拟所得的最大沉降均发生在距离基坑10 m～15 m处，但监测最大沉降为15.75 mm，而模拟最大沉降为6.84 mm，模拟所得的最大沉降明显小于监测结果，可能是由于模拟中各土层均为均质土体，而实际工程中土体属性较为复杂以及实际监测时仪表的架设、周边车辆荷载的影响等，但是两者曲线变化趋势基本一致，均在距离基坑10～15 m处发生最大沉降且呈现为中间沉降大、两边沉降小的趋势。

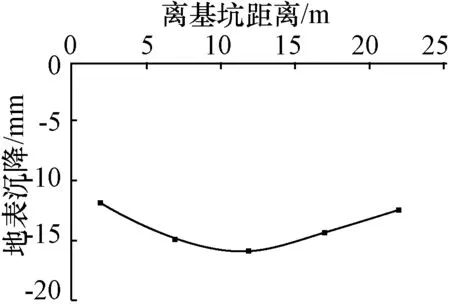
图5 监测数据

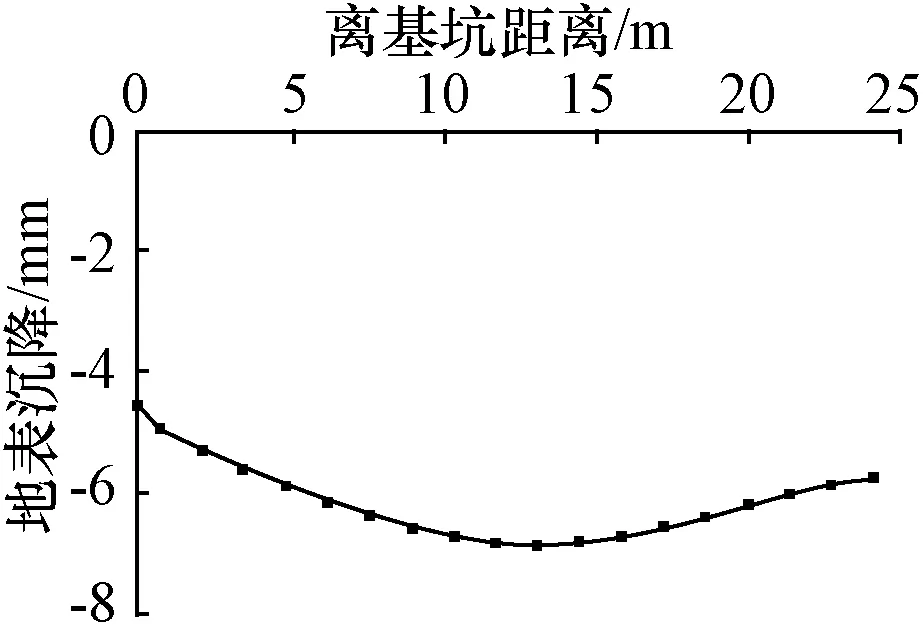
图6 模拟数据

综上所述，虽然地连墙水平位移和地表沉降的监测数据与模拟数据存在偏差，但是两者数据的变化趋势基本一致，这说明本文建立的模型和材料参数的选取较为合理，能够较为准确的反映地下连续墙以及围护结构后地表在基坑开挖过程中的变形规律。

4 基坑开挖与临近地铁隧道的相互影响

4.1 基坑开挖对地铁隧道变形的影响

图7为模拟所得各工况地铁隧道位移值，图8～9为放大变形系数后的地铁隧道变形图，其主要为研究基坑开挖对地铁隧道变形的影响，以确保地铁的正常运营。

图8 左侧隧道变形

图9 右侧隧道变形

从图7可以看出，隧道的变形随着基坑开挖深度的增加而增加，且隧道的水平、竖向位移及径向收敛绝对值均未超过10 mm，均在预警值范围内，进一步表明了本文模拟的合理性。从隧道各点的水平及竖向位移数据可以得出，两个隧道在基坑开挖过程中逐渐向坑内移动且逐渐下沉；无论是左侧隧道还是右侧隧道，水平位移均大于竖向位移，说明位于基坑侧方隧道的变形以横向变形为主；距离基坑较近的右侧隧道各点数据在开挖过程中均大于左侧隧道。从图8～9可以看出，右侧隧道的变形已呈现为斜向“鸭蛋状”，而左侧隧道变形远远小于右侧隧道，这充分证明地铁隧道离基坑越近，越易受到基坑开挖的影响，因此，需对地铁隧道周边环境进行合理规划，避免在地铁隧道附近进行基坑工程，同时对临近地铁隧道的基坑工程的变形进行严格控制，以防止对地铁隧道产生不利影响。

4.2 地铁隧道对基坑开挖的影响

为研究地铁隧道对基坑开挖的影响，将基坑有隧道侧的地连墙水平位移与无隧道侧的地连墙水平位移进行对比。图10～11分别为基坑两侧的地连墙变形。

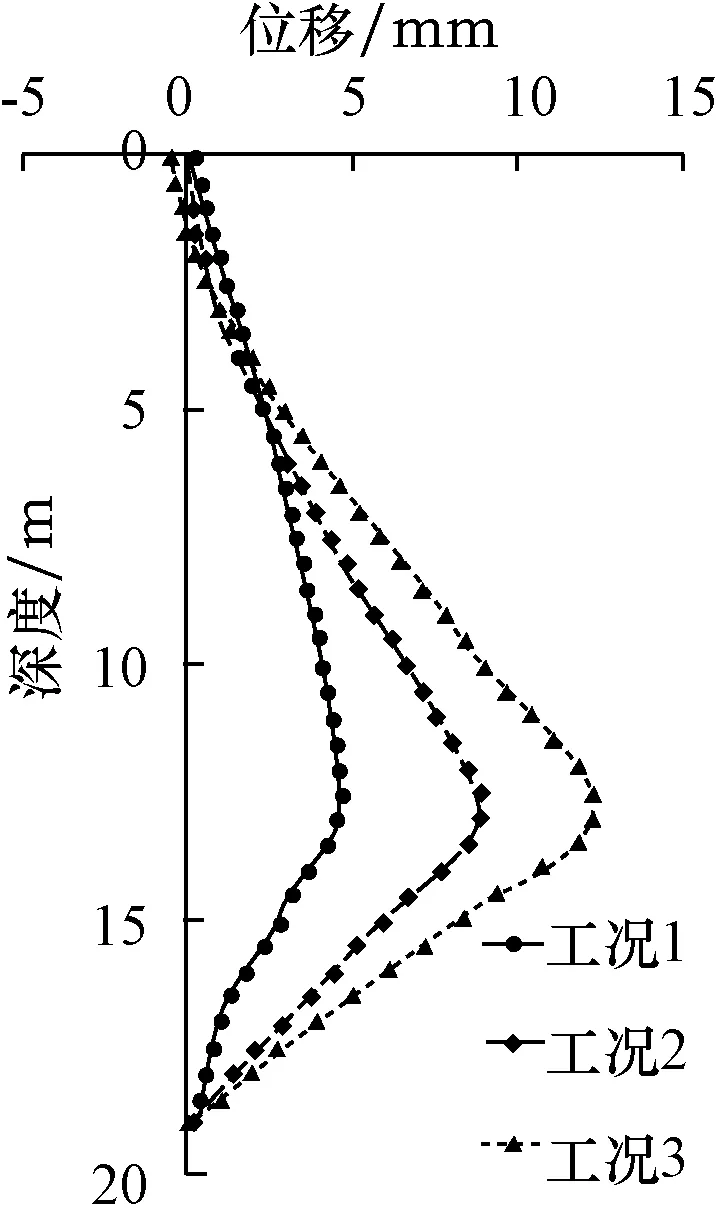
图10 有隧道侧地连墙变形

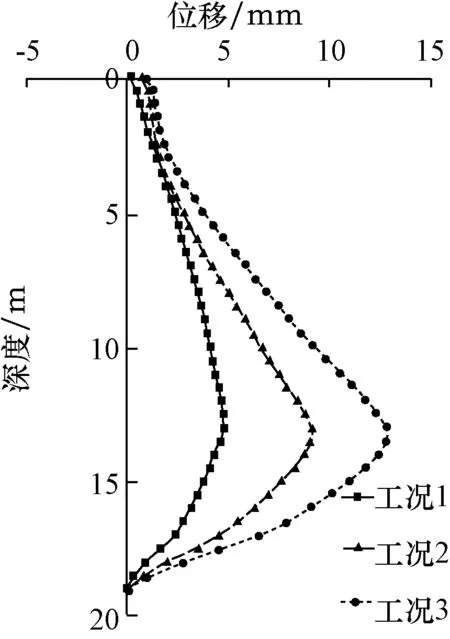
图11 无隧道侧地连墙变形

从图10～11中可以看出，两侧的地下连续墙变形均呈抛物线状，且均向基坑内侧移动。最大位移均发生在深度为12 m左右处，最大位移均在15 mm以内，均在控制范围内。两侧地连墙水平位移无显著差别，在围护结构顶部位置有细微差距，有地铁隧道侧的地连墙顶部有向坑外移动的趋势，由对比结果可得，地铁隧道对基坑开挖的影响是较小的。但为保证地铁的安全运营，仍需严格控制有地铁隧道侧的基坑变形。

4.3 地铁荷载对地连墙沉降的影响

参考前人研究成果[7]，列车荷载可以用一个激振力函数来模拟，具体表达式如下：

F(t)=A0+A1sinω1t+A2sinω2t+A3sinω3t

(1)

Ai=M0αiωi2

(2)

(3)

式中，A0为列车静载；A1，A2，A3为振动荷载；M0为列车簧下质量；αi为正矢值；ωi为振动圆频率；v为列车运营速度；L为振动波长。

苏州轨道1号线各参数别为M0=750 Kg,A0=80 kN,ν=80 km/h,L1=10 m,α1=3.5 mm,L2=2 m,α2=0.4 mm,L3=0.5 m,α3=0.08 mm[8]。由上述公式计算得到如图12所示的列车振动荷载时程曲线。

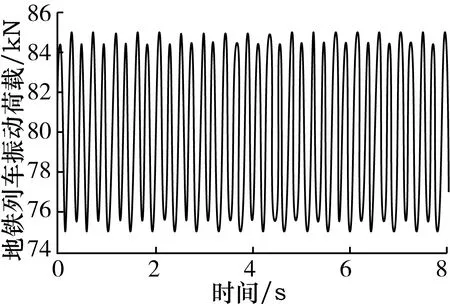
图12 列车振动时程变化曲线

图13为列车振动荷载下的地连墙顶部沉降。从图13中可以看出，地连墙顶部沉降量随着地铁振动荷载的波动而上下波动，沉降量波动范围在6.02～6.61 mm，而未施加地铁振动荷载沉降量为6.4 mm，说明地铁振动荷载会使地下连续墙产生上下浮动的变化趋势，且最大沉降量有所增加，表明地铁振动荷载在一定范围内不利于基坑围护结构变形的控制。

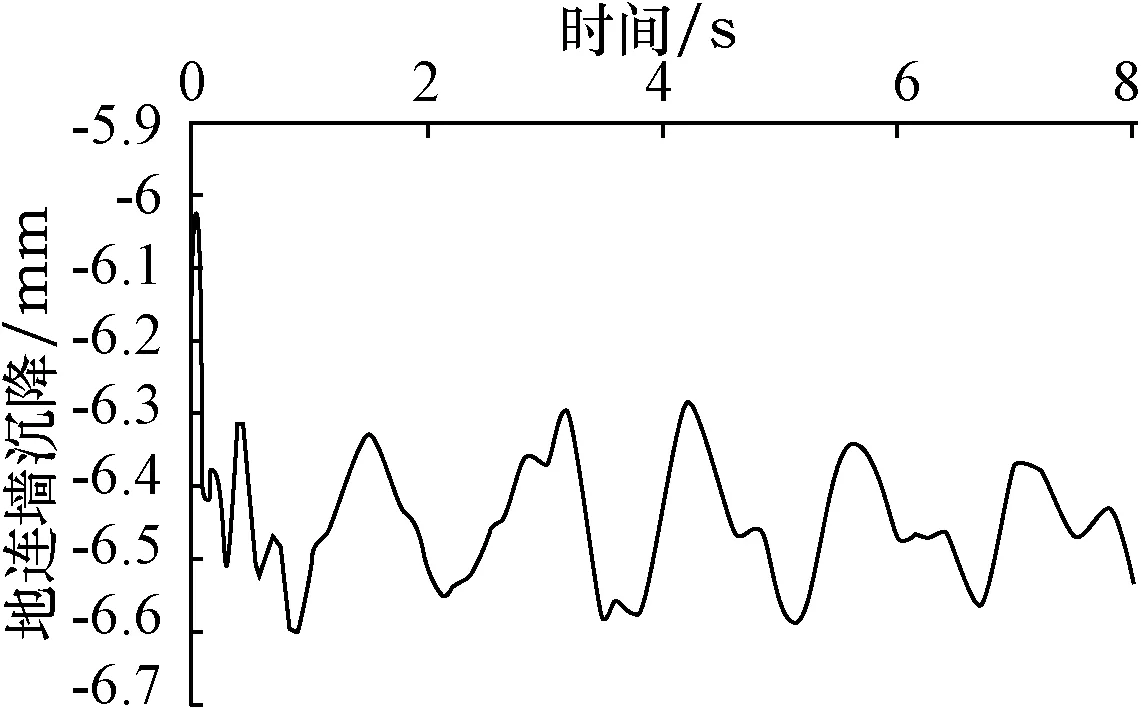
图13 地铁振动荷载下的地连墙沉降

5 结 论

1)模拟所得的地连墙最大位移发生在深度13 m处，最大位移为12.21 mm,而实际工程却发生在深度10 m处，最大位移为9.73 mm；监测与模拟所得的地表最大沉降均发生在距离基坑10～15 m处，但监测最大沉降为15.75 mm，而模拟最大沉降为6.84 mm。虽然监测数据与模拟数据存在偏差，但是模拟曲线与监测曲线变化趋势，表明本文建立的模型较为合理。

2)地铁隧道的变形随着开挖深度的增加而不断加大；地铁隧道在开挖过程中呈现出逐渐向基底移动且逐渐下沉的趋势；地铁隧道离基坑越近，越易受到基坑开挖的影响，而地铁隧道的存在几乎对基坑开挖没有影响，但仍需严格控制有地铁隧道侧的基坑变形。因此，需合理规划地铁隧道周边建筑以及严格控制临近地铁隧道的基坑工程的变形，以保证地铁隧道的安全运营。

3)围护结构竖向变形会受到地铁振动荷载的影响而产生上下波动的趋势，同时会使地连墙的沉降量增大，这加大了对围护结构变形控制的难度。

[ID:010456]