指向深度学习的数学课堂“追问”设计
2020-11-30唐永
□唐永
(江阴市第一中学,江苏江阴214400)
“深度学习”是一个与“浅层学习”相对的概念,反对孤立记忆、机械训练和非批判性接受知识,重视知识的关联、整合与批判性建构,重视学习迁移与问题解决,是一种以发展高阶思维、关键能力为价值取向的学习方式[1].
思维始于问题,而追问能引领思维,助推实现深度学习.“追问”是追根究底地查问,多次地问.这就需要教师运用智慧,对学生初始问题的回答做出准确的判断,及时捕捉契机,设计一系列问题提问.教学中通过“环环相扣”“步步推进”的追问,促使学生改变被动应付的浅层学习方式,引领学生积极思维、持续思维、深度思维,促进学生探究知识本质,从而走向基于理解、迁移应用的深度学习状态,最终达到发展学生思维的目的.
一、在概念建构中追问:把握本质,促进整体理解
深度学习是有意义的学习,不是简单被动的接受,而是积极主动的同化;深度学习更是理解性学习,通过切身的体验和深入的思考,实现对知识意义的深度理解.数学概念是思维的重要形式之一,概念的理解是数学理解的基础,数学概念学习呼唤深度学习.当我们完成概念的引入,学生对概念还处于一个感性认识阶段,没有在同化的基础上实现概念的顺应,没有上升到理性认识,还谈不上理解.此时就需要“趁热打铁”,对学生进行一系列的追问,倒逼、点燃他们的思维,促使他们把握概念的本质,实现对概念的深度建构和整体理解.
案例1“函数的单调性”教学片段
追问1:在区间I内取两个值x1,x2,如x1=1,x2=2,有f(1)<f(2),则函数f(x)在区间I上是增函数吗?
意图:让学生通过举反例来说明.假如f(1)<f(2)<f(1.5),函数图象在[1,2]上有可能凸起,也可能先凸后凹等多种可能,但图象是不会一致上升的.用反例来揭示单调性概念的“任意性”,从正、反两个方面理解“任意性”,有助于培养学生思维的深刻性.
追问2:对于区间I上的任意的x1,x2,当x1<x2时,都有f(x1)<f(x2),则f(x)在区间I上单调递增.反之,成立吗?
意图:单调性概念形成过程中,缺少逆向问题,概念的形成不完备.从反面角度说明这个概念即可以作为判定定理,也可以作为性质定理,是充要条件,具有完备性,它有利于知识的拓展迁移和应用.
追问3:“函数f(x)在区间I上单调递增”和“>0”及“(x1-x2)[f(x1)-f(x2)]>0”等价吗?
意图:挖掘概念的内涵,寻找概念的其他变形、等价形式.
追问4:若定义在区间[a,b]上的函数f(x)在区间[a,c]上是增函数,在区间[c,b]上也是增函数,则函数在区间[a,b]上是增函数.这个说法正确吗?若把区间[c,b]改成区间(c,b],上述说法又会怎样呢?
意图:让学生画图观察,从“形”的角度,建立或健全与增函数或减函数相对应的图象特征.尤其是对一类特殊函数——分段函数的单调性判断做铺垫,而这恰是学生后期最容易犯错的地方.
[评析]单调性是函数的重要性质,其形式化定义是教学的难点.借助追问,把抽象定义具体化、直观化,促进学生从“正”和“反”、“数”和“形”,多角度地把握单调性概念的数学本质,实现整体理解.
二、在公式(定理)推导中追问:搭建思维支架,促进迁移应用
深度学习提倡学生把学过的知识、方法迁移应用到新的问题情境之中,形成解决问题的策略和方案,在问题解决中批判性地学习新知识、掌握新方法,并整合到原有的认知结构中.这就是思维过程中的“感知—决策—行动”,如此循环往复,从而推动认知思维以迭代的方式不断向前发展或是升级.
案例2“等差数列前n项和公式”的教学片段
问题:如何计算S=1+2+…+100=?
生1:利用高斯加法,S=1+2+…+100=(1+100)+(2+99)+…+(50+51)=101×50=5050.
追问1:高斯加法是一种什么算法?它的本质又是什么?
师生互动:高斯加法就是首尾配对法,将不同数的求和问题转化为相同数的求和问题,这时加法运算就上升到乘法的运算,是一种飞跃.
追问2:如何计算Sn=1+2+3+…+n=?
生2:当n是偶数,Sn=1+2+3+…+n=.当n是奇数,Sn=1+2+3+…+n=[1+2+3+…+n+(n+1)]-.
追问3:不讨论能计算吗?
师生活动:当n是偶数,Sn=1+2+3+…+n可以通过配对分组计算,但是,n是奇数时就无法直接配对分组,所以,必须对Sn=1+2+3+…+n进行加工改造,确保是偶数个数的和.学生经过思考、讨论,发现两边再加一个(1+2+3+…+n),即2Sn=(1+2+3+…+n)+(1+2+3+…+n)=(1+n)+(2+n-1)+…+(n+1),实现了配对分组,转化为n个(n+1)的和.
追问4:你能利用上述方法求一般等差数列{an}的前n项和吗?能给它起个名字吗?
追问5:从通项公式an=a1+(n-1)d出发,你能利用倒序相加法再次求等差数列的前n项和吗?
[评析]“迁移与应用”是判断深度学习是否真正发生的主要依据之一.等差数列前n项和公式的推导教学中,针对学生对高斯加法的认知窄化,设计了5个恰时恰点的追问,搭建思维的支架,让学生“知其一也要知其二”,使学生在深刻理解高斯加法本质(配对分组)的基础上,自主迁移应用到等差数列的求和问题中,形成新的方法——倒序相加法.
三、在性质探究中追问:溯本探源,构建深度联系
奥苏贝尔的认知同化学习理论认为,深度学习是对认知结构中现有的信息要素进行重新组合的过程,是构建内在联系的过程[2].这一理论告诉我们,在数学教学过程中,要注重寻找核心知识与思想方法之间的内在逻辑线索,并构建深度联系.
案例3“椭圆的几何性质——离心率”的引入片段
生1:一个圆一点,一个扁一点.
追问1:可以用什么量刻画椭圆的圆与扁的程度?
追问2:很有道理!但是椭圆定义中只涉及a、c两个原始量,是本源的参数,而b是后来推导椭圆标准方程时引入的参数,能否用含a和c的一个量刻画椭圆的“扁”的程度?
教师用几何画板演示,设置两种按钮:(1)固定2a,变化2c;(2)固定2c,变化2a.
[评析]在这种“追问”式的教学过程中,引导学生溯本探源,分析探寻到刻画椭圆“扁圆”程度的本源量,同时揭示和之间的逻辑关系,形成完整的知识链,建构深度的联系.
四、在问题解决中追问:启发探究,促进思维进阶
布鲁姆的教育目标分类学把教学目标分为六大层次,即识记、理解、应用、分析、综合、评价.其中后面四层对应着深度学习的认知水平,体现问题解决、批判性思维和创造性思维等高阶思维.在问题解决中通过连续的追问,开发出一些本源性数学问题,围绕这些问题将探究引向深入,增强学生思维的深刻性,发展学生的高阶思维能力.
案例4在△ABC中,BC为定长,,若△ABC面积的最大值为2,则边BC的长为________.
师:大部分同学通过建系,计算得到点A的轨迹是一个圆,这是解题的关键.能否不建系,发掘等式直接获得点A的轨迹呢?
生1:如图1,延长AC至D使C为AD中点,取BD中点E,连接AE.设AE∩BC=G,则G为△ABD的重心.根据平行四边形法则,.由得,则,因为为定长,所以点A的轨迹是以G为圆心,|长为半径的圆.
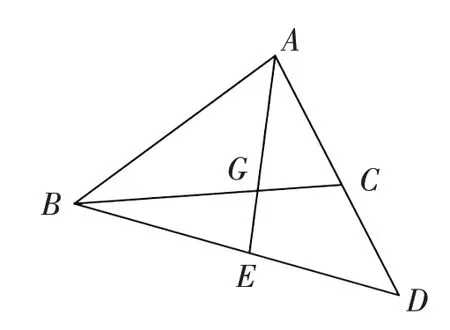
图1
追问2:从向量的系数来看1+2=3,还可作怎样变形?
生2:模的平方处理.
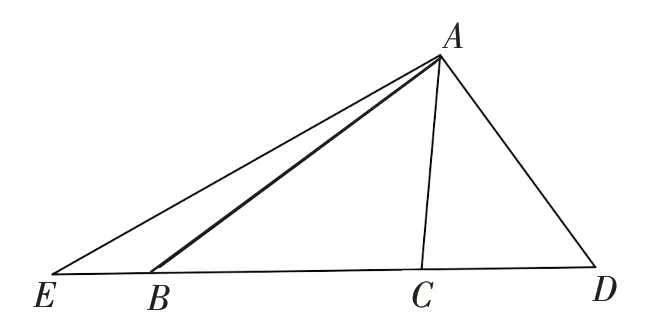
图2
[评析]问题是深度学习的载体,深度学习的过程往往是围绕着具有挑战性的问题开展的探究性活动过程.从不同的角度对条件“ |”展开追问,生成三个本源性问题,启发学生探究,获取更多的方法,在提升学生综合运用知识能力的同时发展创造性思维.
总之,追问是教师和学生之间的深度对话.要在充分理解教材、理解学生、理解教学的基础上设计追问,要在学生思维的瓶颈堵塞点、转化链接点、拓展放射点上适时、适度地追问,不断将课堂学习推向更深层次的有意义、理解性学习,这样才能让课堂更加充满活力,才能让深度学习更有燃点和沸点.□◢
