根键桩抗拔位移场分布特征及荷载传递模型探究

张吉禄，黄雪峰,2，韦林辉，周俊鹏，袁 俊，王学明

(1.兰州理工大学 土木工程学院，甘肃 兰州 730050; 2.重庆交通大学 土木工程学院，重庆 400074; 3.陆军勤务学院 军事设施工程系，重庆 401311; 4.中国电力工程顾问集团 西北电力设计院有限公司，陕西 西安 710075)

对基础承载特性的深入探究有助于指导工程实践根据不同现场条件选择不同基础类型，以确保工程的安全性以及经济效益。针对基础抗拔领域，随着工程建设需求的提高，基础承载力设计值大幅提升，以等截面桩为主的摩擦型桩由于其承载力仅由侧摩阻力提供，经济效益随承载力需求的提高而逐渐降低，因此，近年来诸多截面异形桩如雨后春笋般涌现[1-3]，截面异形桩由于变截面法向阻力的作用，在增加较小材料用量的同时大幅提高了基础承载力，但是诸如扩底桩或支盘桩多数情况下需人工掏挖成孔或爆破成孔，随着基础深度的增加，人工掏孔的安全问题尤为突出[4-5]，而爆破目前并不能适用于所有地质条件，且变截面处无法设置钢筋，在抗拔过程中有可能发生混凝土塑性破坏的危险，而根键桩作为近几年新出现的变截面桩[6]，其无需大面积掏挖，根键与桩身通过钢筋连接且对地质条件适应能力强等优点逐渐被业界所接受，但是对其抗拔承载机理的研究目前较为匮乏，理论成果尚不足以指导工程实践。因此，对于不同截面形式抗拔基础承载特性以及适用范围的探究已成为目前桩基领域热门问题之一。

近年来，诸多学者针对不同截面形式抗拔桩承载特性进行了系列研究，并取得了一定成果，其中主要包括理论推导、现场试验、数值模拟以及室内模型试验。对于室内模型试验方面，王钦科等[7]通过离心模型试验对上覆土嵌岩扩底桩的承载特性以及岩体破坏规律进行深入分析，并通过极限平衡理论提出一种简化的承载力计算方法;曹卫平等[8]为探究抗拔斜桩承载特性及荷载传递机理对埋置于砂土中的模型桩进行抗拔试验，结果表明:斜桩承载力受桩身倾角及长径比影响，且斜桩桩身上部存在弯矩及剪力，斜桩最大弯矩亦受倾角及长径比影响;葛楠等[9]对砂土中根键桩的抗拔特性进行了模型试验，对根键桩承载能力以及桩身荷载传递规律进行了初探，但是关于桩土作用规律以及土体实时位移资料传统室内模型方法无法获得，这严重制约了抗拔基础作用机理的进一步探究。

随着ISKANDER等[10]利用无定型硅与具有相同折射率的孔隙液体合成与天然土具有相似性质的透明土，可视化研究桩基承载特性中位移场发展规律成为可能。WHITE等[11]采用透明土与PIV(粒子图像测速技术)相结合的技术测得了半桩沉桩过程中桩周土体位移场;NI等[12]通过PIV与透明土技术对圆桩沉桩过程的挤土效应进行了分析;此外，国内学者也对该技术在室内模型试验中的应用做了大量研究，如孔刚强等[13]利用透明土与PIV技术测定了扩大头对楔形桩位移场的影响;曹兆虎等[14]基于透明土与PIV技术分析了不同截面形式的异形桩上拔过程中的位移场发展规律;周航[15]、齐昌广等[16]也分别在PIV与透明土技术的支持下对不同形式桩的桩土作用机理展开了深入的研究。但是上述试验多集中于桩土运动规律的定性研究，由于小尺寸模型桩-土界面摩阻力难以测定，且常用理论公式在小尺寸模型计算中存在较大误差，因此PIV与透明土技术在精确分析桩土荷载传递规律方面还未形成有效的理论体系。

笔者基于透明土与PIV技术采用非介入式量测方法开展竖向荷载下根键桩抗拔模型试验，通过与等截面桩、扩底桩承载能力以及位移场发展趋势的对比确定根键桩工程适用范围以及桩土作用规律的特点，并进一步基于透明土特性研究成果对根键桩与等截面桩及扩底桩的荷载传递规律进行计算分析，为根键桩的工程应用提供参考依据。

1 模型试验概况

1.1 试验设备

图1为试验布置图，其中激光器型号为DR-532CP-5型片光激光器，试验功率为2.2 W，试验中图像的实时记录由CCD高速工业相机完成，经调节本试验相机最优分辨率为1 920×1 080。此外，试验所用模型槽为长方体透明有机玻璃槽，考虑到上拔过程中引起的土体位移，为保证玻璃槽的边界约束不会对土体位移的发展造成明显影响，综合现有研究资料[17]，选取模型槽宽度>10D(D为模型桩直径)，平面尺寸为150 mm×150 mm，高190 mm，壁厚5 mm，模型槽中间印有刻度线，以方便模型桩的对中以及PIV图像处理。

1.2 透明土及制备方法

现有研究[18-19]表明天然砂土与合成透明土具有较为相近的物理力学性质，透明土能够作为砂土替代材料用以探究桩土作用规律。

本试验透明土是由熔融石英砂与具有相同折射率的混合液体组成，其中熔融石英砂干密度为0.970～1.274 g/cm3，混合后实测透明土密度为1.05 g/cm3，密实度约为50%，黏聚力c=0，摩擦角φ=38°，弹性模量以及泊松比根据现有研究资料[20]可取E=30 MPa，ν=0.3，试验全程室温控制在24 ℃左右，其制备过程如图2所示。

1.3 试验模型桩设计及制作

模型桩桩身具体参数见表1，所有模型桩全长均为185 mm，桩底至地表高度均为100 mm。对于根键桩而言，每层变截面均由6根根键等角度组成，根键外伸长×高×厚为6 mm×3 mm×3 mm。

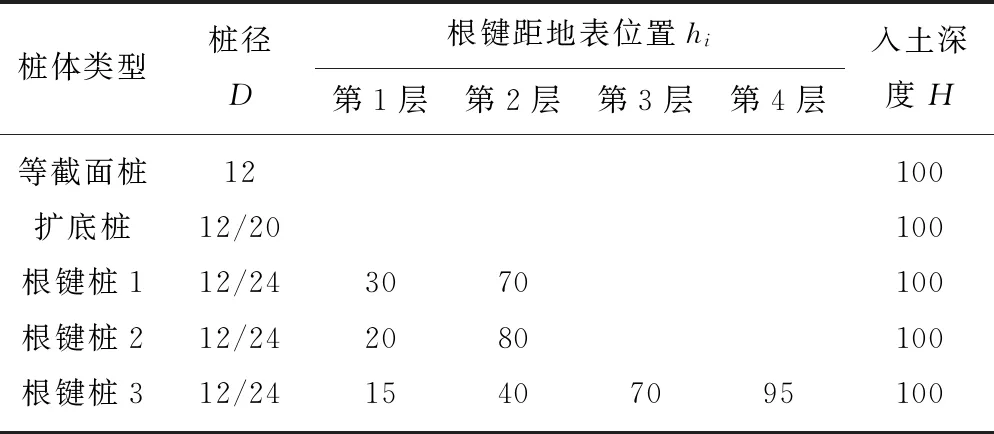
表1 桩身参数Table 1 Pile parameter mm

为降低材料表面激光散射所造成的试验误差，本文所用模型桩由黑色环氧树脂制成，其密度约为2.3 g/cm3，弹性模量为1 GPa，在试验条件下可忽略模型桩变形影响，且为增大桩身侧摩阻力，已将模型桩周均匀黏贴一层与透明土相同规格熔融石英砂，模型桩实物及尺寸如图3所示。

图3 模型桩设计示意及实物Fig.3 Diagram and physical diagram of model pile

1.4 试验目的和过程

为系统研究抗拔桩承载特性变化规律，基于PIV与透明土技术对等截面桩、扩底桩以及不同形式根键桩进行抗拔试验。试验过程主要分为2个阶段:① 实验前准备阶段;② 实验加载及数据获取阶段。

(1)实验准备阶段主要是透明土的铺设与模型桩的安置，首先将透明土均匀摊铺至60 mm厚，以确保模型桩与底部边界有足够的空间，之后将模型桩固定于玻璃槽中间并与底部透明土接触，完成固定后继续摊铺透明土至总厚度达到160 mm，透明土摊铺过程中要始终保持混合液体液面高度高于熔融石英砂，且为保证测量准确性，摊铺过程中土中产生的气泡要通过玻璃棒搅拌等方式及时排出，完成上述步骤后静置4～6 h即可开始加载试验。

(2)实验加载及数据获取阶段，为排除外部光源干扰，试验均在无光环境中进行，试验过程首先将片光激光器对准模型桩中心并使之产生稳定散斑场，之后调整DDC相机角度位置使相机垂直于片光散斑场并通过支座固定于操作台，完成上述调整之后对模型桩进行逐级加载，试验采用砝码加载，位移采集通过固定于桩顶电子位移计测量所得，加载方案见表2。待每级荷载下位移达到稳定后使用DDC相机对其位移历程进行拍摄记录，最后采用PIV view2软件对加载前后图像任一点像素位置进行追踪，进而确定某时间段内颗粒移动轨迹，从而形成宏观位移场变化等值线图，即PIV技术，具体图像处理流程如图4所示。

图4 图像处理流程Fig.4 Flow chart of image processing

表2 模型桩加载方案Table 2 Loading scheme of model piles

2 模型桩承载特性对比分析

2.1 Q-S曲线对比分析

试验规定模型桩拔出前一级荷载为抗拔极限荷载，其桩顶荷载-位移(Q-S)关系曲线如图5所示。

由图5可知，5个模型桩极限荷载分别为6.5，11.0，8.0，8.5，10.0 N。曲线发展规律均可划分为2个阶段，当荷载较小时，位移随荷载基本为线性增加，随着荷载的进一步增加，位移的发展均表现出不同程度的非线性增长趋势，其中等截面桩非线性增长趋势出现最早，其承载力最小;而扩底桩虽然承载能力最高，但是在加载前期，根键桩3对基础位移的控制能力最为突出，由此看出，虽然实验条件下相同尺寸根键桩3承载力略小于扩底桩，但是根键桩通过多层变截面的设置，在一定荷载范围内对基础位移的抑制起到了显著的作用，对于诸如输电线路杆塔此类对基础位移有严格要求的建筑而言，根键桩在此类工程中的应用具有明显优势与特点。

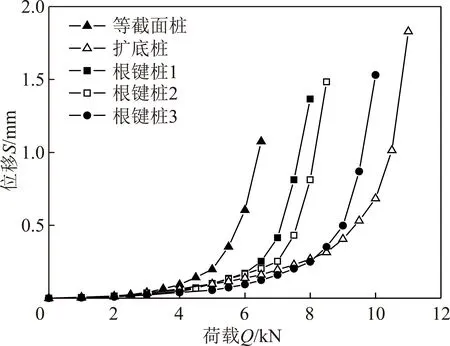
图5 桩顶荷载-位移关系曲线Fig.5 Relationship curves of load-displacement of piles top

进一步对根键桩1,2对比可知，虽然两桩由于根键层数较少的原因，无论在极限承载力还是对基础位移的控制上均弱于根键桩3以及扩底桩，但相比等截面桩承载力仍有23%，30%的显著提升，且通过对比还可看出，相比于根键桩1，根键桩2根键间距更大，埋置深度更深，说明根键承载力的充分发挥需要充足的纵向空间，对于一些更侧重于极限承载力而对基础位移控制要求较弱的建筑而言，将根键埋深适当增加不失为一种更为经济的思路。

2.2 相似理论验证分析

由于模型试验为1 g模型(在常重力中进行的小比例尺试验)，其尺寸缩小n倍，则荷载及位移等测试数据均对应足尺试验的1/n，但材料物理力学性质应与现场试验相同。由于目前尚未发现相同条件与尺寸的现场足尺试验，故选取文献[21]中具有相近长径比现场试验进行相似性分析。

模型试验与现场试验各参数对应关系已列于表3，表中，ρz为试桩密度;Ez为试桩弹性模量;ρt为土体密度;Et为土体压缩模量;c为黏聚力;φ为内摩擦角，其中文献扩底桩A5扩大头与桩径比为2.25，而模型桩为1.67。模型与文献相似比为n=66.7，桩周侧阻力发挥情况主要由式(1)决定，即侧摩阻力与土体密度线性相关，而透明土本身性质与制备条件所限无法达到文献所述相同密度水平，故将原相似比n乘两土体密度比0.64来消除土体性质差异带来的试验误差;由于模型试验均为低应力水平，因此本文并未将试桩变形考虑在内，故试桩物理参数带来的差异可忽略不计。

表3 模型与文献试验参数Table 3 Parameter of modeltest and literature

τ=μγhK

(1)

式中，τ为侧摩阻力;μ为桩土摩擦因数;γ为土体容重;h为计算深度;K为土压力系数。

图6为通过相似计算将模型桩换算为与文献同直径状态下各桩Q-S曲线对比情况，由图6可知，对于两等截面桩而言，其长径比最为接近，且桩周只存在侧摩阻力，受力形式较为单一，两曲线无论在发展形式还是荷载、位移数值上均较为接近;而两扩底桩在发展规律方面虽较为相似，但是由于文献扩大头尺寸比明显大于本文模型桩，且土体性质亦存在一定差异，导致曲线在小荷载时有较高吻合度，但随着荷载的增加，曲线位移表现出较明显差异，但总体而言，通过相似比计算得到的模型Q-S曲线与文献曲线仍处于相近的荷载水平，且由于模型扩大头与文献尺寸差异而导致曲线在一定程度上高于文献扩底桩也是合理的发展趋势。

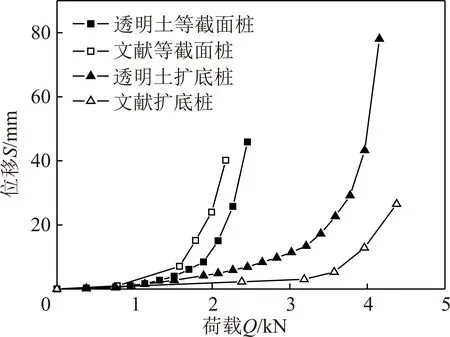
图6 模型相似计算与文献Q-S曲线对比Fig.6 Comparison between model similarity compulation and literature Q-S curves

综上所述，通过相似计算与现有研究文献实测数据对比在一定程度上验证了透明土模型试验的可信度，试验所得结果能够正确反映基础承载性能发展规律，可为工程实践提供相关指导。

3 基于PIV的桩周土体位移场分析

3.1 桩周土体位移场等值线对比分析

图7为4 N荷载下桩周土体位移等值线图，其中等值线增量为0.01 mm。图8为极限荷载下桩周土体位移等值线图，等值线增量为0.05 mm，其中，α，β，γ1，γ2，γ3为各试桩在极限荷载下位移场边界与水平面夹角。由图分析可知，桩周土体位移场无论强度还范围均随上部荷载的增加而扩大。4 N荷载下各桩桩周土体最大位移分别为0.10，0.08，0.07,0.05，0.05 mm，由于等截面桩侧摩阻力发挥程度要大于同荷载下其他模型桩，故其桩周土体位移最为明显，扩底桩由于扩大头阻力与侧摩阻力发挥的异步性造成在加载前期抑制桩土位移的效果并不明显，而根键桩尤其是根键桩3在小荷载情况下对桩土位移的抑制效果则比较明显，且从图7也可看出，即使在小荷载情况下，不同位置处根键均较明显的发挥了阻力作用，有效降低了侧摩阻力的发挥，这也进一步印证了第2节对于根键桩适用范围的建议。

图7 荷载作用下桩周土体竖向位移等值线Fig.7 Contour map of vertical displacement of soil around the pile under the 4N load

对图8极限荷载下各桩位移场发挥情况对比可知，此时各桩最大位移分别为0.40，0.85，0.70，0.75，0.85 mm，根键桩3与扩底桩的桩周土体最大位移已达等截面桩的2.1倍，而根键桩1,2也分别达到1.8与1.9倍，由此可以看出变截面的设置对改变桩土受力模式，进一步发挥土体承载能力起到了至关重要的作用，且基础达到极限荷载时，无论基础形式如何改变，桩周土体位移场均为“倒三角形”分布，位移场边界与水平方向夹角依次为:63.5°，67°，65°，62°，64°，基本符合摩尔库伦经典理论中剪切破坏滑裂面与水平方向夹角(45°+φ/2)的关系。

图8 极限荷载向下桩周土体竖向位移等值线Fig.8 Contour map of vertical displacement of soil around the pile under the ultimate load

进一步通过对比3组根键桩可以看出，多层根键的均匀布置可以使土体承载力得到更大程度的发挥，而当根键层数较少时(纵向密度较低)，由于部分根键周围土体较早发生塑性破坏，而无其他根键进行补充，因而土体承载力无法得到更进一步发挥;另一方面，就不同根键排列方式下各桩桩周土体位移场发展规律而言，根键桩1,2根键周围位移场形成两个明显上下独立的作用区域，且对于根键桩2由于两根键间距过大，桩身中部有较大部分土体位移未得到明显提升;而根键桩3上部两层根键影响区域产生部分重合的趋势，由此可以看出，根键纵向间距过大会导致部分土体承载力得不到进一步发挥，而间距过小会使两位移场产生叠加，进而过早发生塑性破坏，因此，根据本文试验结果，初步建议根键纵向间距应以(4～6)L为宜(L为根键外伸长度)。

3.2 桩周土体位移场的像素面积对比分析

为进一步定量描述不同基础位移场的变化情况，将图7,8转换为相同尺寸大小图片(357×579)，之后通过图像处理软件对不同色阶的像素点进行统计，进而得到不同状态下位移场像素点数，如有需要也可通过等比放大，从而得到足尺试验状态下土体各位移梯度的截面积或体积，在目前现场试验技术手段还不能精确测量土体位移场情况下，基于透明土与PIV技术的像素计算能够较准确反映桩土作用规律的同时进一步定性分析各状态下土体位移场变化情况，这是传统理论计算或数值模拟所不具备的优势。

通过计算，将图7，8各桩位移场面积列于表4。由表4可知，当上拔荷载为4 N时，扩底桩位移场面积基本与等截面桩相等，这与扩底桩阻力发挥的异步性直接相关;而根键桩1,2位移场面积较等截面桩有明显降低，说明在小荷载下，上部荷载已有相当一部分由根键阻力承担，从而导致侧阻发挥程度较低，故削弱了位移场的影响范围;而根键桩3由于多层变截面的设置，虽然侧摩阻力的抑制程度要更高于根键桩1,2，但是根键所起到的对土中荷载的分散作用得到显著增强，故总体表现出位移场面积提高的现象;而极限荷载下，扩底桩扩大头阻力得到了充分发挥，位移场面积得到较大提升，但是相比根键桩3仍有较大差距，因而扩底桩对土体承载力的发挥程度要弱于多层变截面的根键桩3，而根键桩1,2此时位移场面积与等截面桩较为接近，由此看出，当根键纵向密度较小时，虽然根键的植入对基础承载力有一定提升作用，但是根键对荷载的扩散作用并不明显，因而无法达到使更大范围土体共同受力的目的。

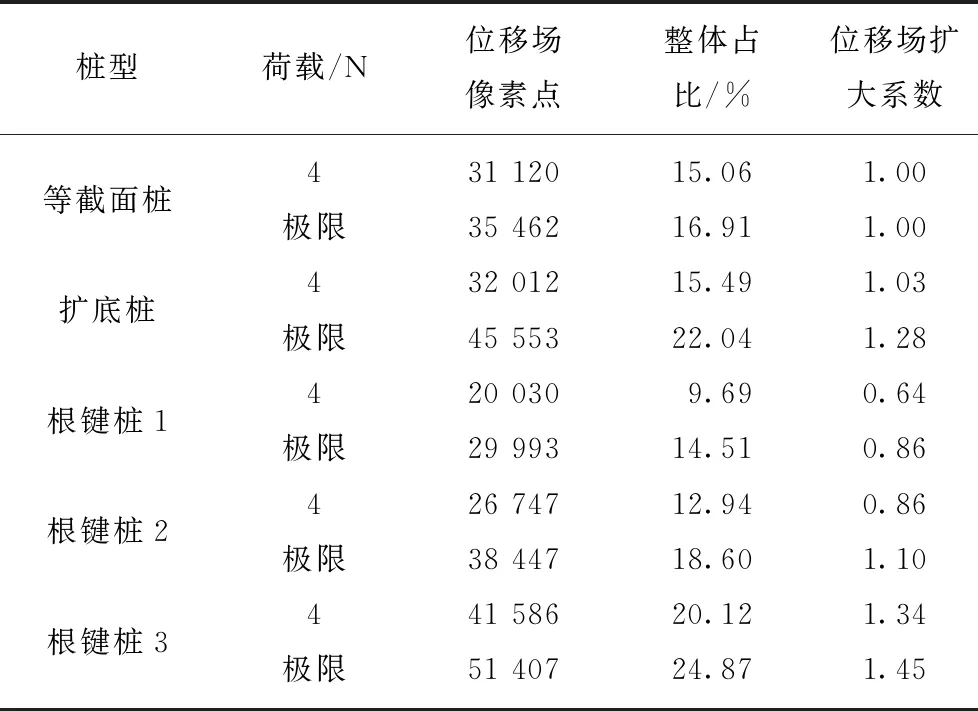
表4 土体位移场参数Table 4 Parameter table of soil displacement field

3.3 塑性区位移场分析

图9为孔刚强等[19]对透明土变形特性三轴试验中密实度Dr分别为30%与70%的透明土不同围压下剪切应力-应变关系曲线。

图9 文献[19]不同围压的应力-应变曲线Fig.9 Document 19 stress-strain curves under different confining pressures

沿用土力学中土的剪切破坏理论，将30%与70%密实度不同围压土体应变屈服点绘成如图10所示围压-屈服应变趋势图，通过拟合得30%与70%密实度围压τ30,τ70与屈服应变ε关系式为

图10 不同密实度下围压与屈服应变关系Fig.10 Curves of relationship between confining pressure and critical strain under different densities

τ30=2 015.8ε3-4 741.5ε2+3 782.4ε-846.45

(2)

τ70=1 479.7ε3-3 168.3ε2+2 265.2ε-364.97

(3)

桩侧土压力为

σ=Kγh

(4)

式中，松砂的土压力系数K=Ka，中密砂的土压力系数K=K0，密砂土压力系数K=Kp[22],Ka,Ko,Kp分别为主动、静止、被动土压力系数;γ为透明土容重;h为桩体入土深度。

经计算得30%与70%密实度下屈服应变分别为0.365 2×10-2，0.226×10-2。本文砂土密实度大约为40%，故将上述屈服应变线性内插后约为0.3%，剪切式样高度为80 mm，将其换算为剪切位移量为0.24 mm。

通过土体屈服位移的确定得到等截面桩、扩底桩以及根键桩3塑性区水平向最大影响范围分别为:1.5R，4R，4R(R为桩身半径)。说明在加卸载过程中桩周土体产生不可恢复变形的最大范围由于变截面的引入明显增大，荷载沿水平方向的传递能力提升显著(鉴于文章篇幅所限，下文分析中仅选取特点最突出的根键桩3为代表对根键桩承载特性做进一步分析)。

进一步对图8极限荷载下不同桩型塑性区位移场面积进行像素计算得表5，由表5分析可知，位移场总面积大小依次为:根键桩>扩底桩>等截面桩，而3桩塑性区面积大小依次为:扩底桩>根键桩>等截面桩，且扩底桩塑性区在位移场总面积中占比最大，达到51.2%，而根键桩仅为26.4%，变截面的植入对土体承载能力的改善是显而易见的，但是不同变截面形式其承载能力提升效果却也差距明显，其中根键桩塑性区面积仅为扩底桩的58%，但是位移场总面积达到扩底桩的113%，这主要是因为实验条件根键密度不大，导致根键附近荷载集中程度要高于扩底桩，因此，不难想象随着根键密度的提升其承载能力提升空间显然要优于扩底桩。

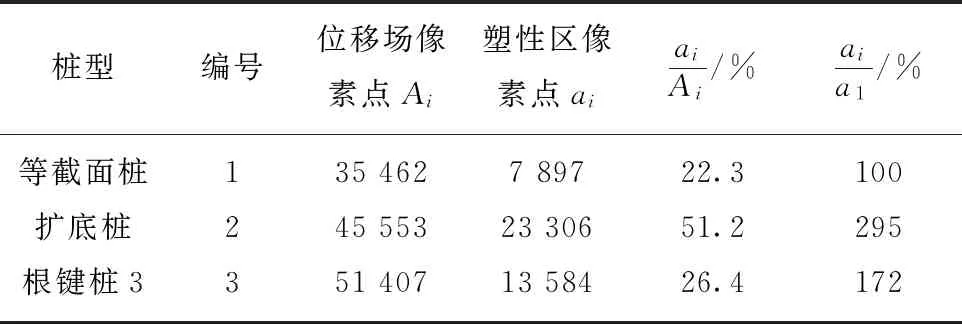
表5 极限荷载下土体塑性区像素面积Table 5 Pixel area table of plastic zone of soil under limit load

4 桩土侧阻力分析

4.1 侧阻力计算分析

对文献[19]透明土剪切应力-应变发展规律分析可知，在达到最大剪应力前曲线符合对数函数或幂函数的发展规律，由于上述函数无法反应应变软化问题，故仅取达到极限之前曲线进行拟合，发现对数函数式(5)拟合度相对更高，其中a，b均为与围压σ3有关的参数。

τ=aln(bε+1)

(5)

进一步对参数a拟合，发现无论Dr=30%或Dr=70%其均符合式(6)发展规律:

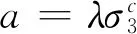
(6)

式中，c为拟合参数。

由摩尔库伦强度理论知，抗剪强度主要由黏聚力以及侧压力产生，由于砂土无黏聚力，故当围压为0时可近似认为τult为0。即边界条件:

δ3=0，τult=0

(7)

式中，τult为极限侧摩阻力;δ3为小主应力。

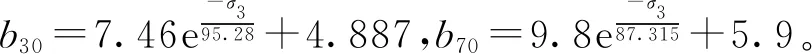
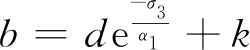
(8)

式中，d，k，α1均为拟合参数。

由此得到了2种密实度情况下的不同围压剪应力应变拟合公式(9),(10)，将式(3)算得到桩侧土压力代入拟合公式，其中K=1-sinφ，φ取37°;之后分别将图8桩侧土体位移转换为三轴试验应变，从而得到两种密实度下桩周侧摩阻力的深度分布，而本文透明土密实度接近40%，故对上述结果采用线性内插法得侧摩阻力分布图。

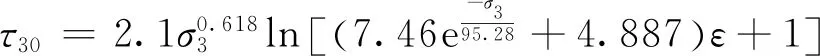
(9)

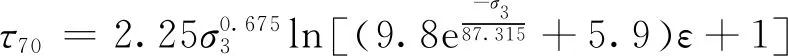
(10)

图11为模型桩侧阻力分布图，图中G1，G2，G3，G4分别代表第1，2，3，4层根键位置。通过对3种桩型极限荷载下侧阻力分布图分析可知，等截面桩侧阻力发挥具有深度效应，峰值发挥深度在0.6h处，大小为2.78 kPa，当深度超过0.6h时，侧阻力发挥基本呈递减趋势，桩端处仅为侧阻力峰值的30%左右;扩底桩桩端处阻力大小为3.29 kPa，且等截面段同等截面桩相似，侧阻力随深度增加而衰减;而根键桩根键阻力作用的发挥亦具有深度效应，在第2层根键处阻力作用达到最大3.53 kPa，第4层根键此时为2.6 kPa，最深处根键阻力作用为峰值的75%左右，深度对根键承载力衰减的影响仅为等截面桩侧摩阻力的35%左右，说明根键与扩大头等变截面的设置均使土体极限承载力得到明显提高，且深度效应对变截面法向阻力的影响远小于侧摩阻力。

4.2 侧阻力计算与试验对比验证

为验证经验公式的可靠性，对上述计算所得阻力进行反算将其转化为上拔荷载并与实际模型试验加载所得极限承载力进行对比。其中等截面桩上部荷载可按式(11)进行计算

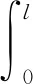
(11)

式中，d为桩身直径;l为桩长;τ(z)为深度z处的剪应力;F为轴力。

扩底桩与根键桩由于变截面的设置可将轴力分为侧摩阻力f与法向阻力f′两部分，具体计算过程为

F=f+f′

(12)

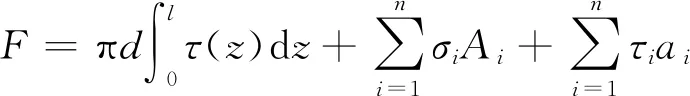
(13)

其中，σi与Ai为第i层变截面处的正应力与法向接触面积;τi与ai为第i层变截面处的剪应力与竖向接触面积;对于扩底桩n=1，而剪应力与正应力的关系如下所示，其中泊松比ν=0.3。

σ=2(1-ν)τ

(14)

将式(14)代入式(13)即可得到扩底桩与根键桩轴力值。具体模型桩极限荷载试验Fs与计算值Fj见表6。

表6 模型桩计算与试验荷载对比Table 6 Comparisons between calculated and measured axial forces of model piles N

由表6可知，计算轴力超过实测轴力25%～35%，这主要由两方面原因造成:① 对桩周土体密实度估算造成的误差;② 由于下部土体变形而造成上部土体位移的累积效应，使桩体上部侧阻力计算结果偏大而造成的误差。总体来说，该拟合公式基本能够定量反映桩土侧阻力的发挥程度，可供小尺寸模型试验中荷载传递的定量分析参考。

5 结 论

(1)通过相似理论对比验证了基于透明土与PIV技术在桩基础面应用的可行性，试验所得结论对工程实践具有一定指导价值。

(2)试验条件下，变截面的设置使基础承载力均有大幅提高，其中扩底桩极限承载力最高，可达等截面桩的1.7倍，但在中低荷载情况下，多层变截面的根键桩对上拔位移的抑制能力最为突出，更适用于对位移有严格控制要求的建筑基础。

(3)不同基础周围土体位移场虽在小荷载下发展形式各不形同，但是到达极限状态时位移场均为“倒三角形”分布，位移场比边界与水平面夹角均为(45°+φ/2)。

(4)根键纵向间距的布置存在优化问题，当间距过小时，两根键之间产生相互作用会削弱承载力发挥，而间距过大会导致桩周部分土体承载力得不到提升，根据本文相初步研究，建议纵向间距以(4～6)L为宜(L为根键外伸长度)。

(5)扩大头的设置使土体承载力得到进一步发挥的同时也在一定程度上扩大了桩周土体受力范围;对于根键桩而言，当根键层数较少时，根键周围应力较为集中，对荷载扩散作用不明显，土体位移场范围相比等截面桩甚至出现小幅降低，而随着根键层数的增多，桩周土体位移场范围也随之显著扩大，在试验条件下，四层根键所带动的土体位移场面积约为扩底桩的113%，而塑性区面积仅为扩底桩的58%，根键桩承载能力提升潜力要优于扩底桩。

(6)通过结合现有透明土三轴试验资料分析得到能够较准确反映透明土承载能力变化规律的侧阻力计算经验公式，其中根键与扩大头的设置分别使土体极限承载力提高了1.27与1.18倍，变截面的设置使土体承载力得到了更大程度发挥，且深度效应对根键法向阻力影响远小于侧摩阻力。