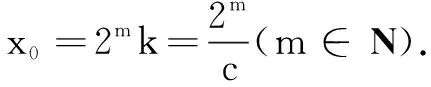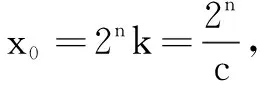一道高考试题的探究历程及感悟*

李 锋

(福建省连江第一中学，350500)

高考试题“源于教材,高于教材”,大多是由教材核心概念、基本知识及相关题目加工改造、延伸拓展而来. 这些试题反映了相应数学核心知识的本质属性,蕴涵了重要的数学思想,有效考查了学生的思维水平、解题能力和学科素养.本文以2014年高考福建理科数学第20题(压轴题)为例，进行探究.

一、真题再现

已知函数f(x)=ex-ax(a为常数)的图象与y轴交于点A,曲线y=f(x)在点A处的切线斜率为-1.

(1)求a的值及函数f(x)的极值;

(2)证明:当x>0时,x2

(3)证明:对任意给定的正数c,总存在x,使得当x∈(x,+∞)时,恒有x2

分析本题主要考查基本初等函数的导数、导数的运算及导数的应用等基础知识,考查运算能力、推理论证能力和抽象概括能力,考查函数与方程思想、有限与无限思想、化归与转化思想、分类与整合思想和特殊与一般思想,考查数学抽象、直观想象、逻辑推理和数学运算等核心素养.

其中第(1)问利用导数求函数极值与第(2)问构造函数、利用导数证明不等式，来源于教材常规的基本知识与基本方法(见人教A版《普通高中课程标准实验教科书·数学》选修2-2“1.3导数在研究函数中的应用”相关知识及习题1.3B组第1题:证明下列不等式(3)ex>1+x,x≠0;(4)lnx0),这里不再赘述.第(3)问解法多样,下面给出几种比较典型的解法.

解法1① 若c≥1,则ex≤cex.由(2)知,当x>0时,x20时,x2

综上,对任意给定的正数c,总存在x0,使得当x∈(x0,+∞)时,x2

二、背景探源

人教A版《普通高中课程标准实验教科书·数学》必修1“3.2函数模型及其应用”中指出,“一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>0),通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn……”显然,教材通过大量的实例,借助信息技术精确呈现出相关函数值的变化,最后直观得出上述关于“不同增长的函数模型”增长趋势的定性描述. 但由于知识受限,无法在理论上予以证明. 学习了“导数及其应用”后,就能够利用导数这个工具进行证明. 2014年福建卷的压轴题的第(3)问,其实质就是来源于上述函数增长模型的比较. 数学是讲道理的,命题的立意是想以这个凭直觉显而易见的结论为载体,突出导数的工具作用,考查学生在解题过程中对“常量”与“变量”辩证关系的理解以及综合运用导数研究函数性质的能力,以推崇数学的理性思维.

三、深度探究

拓展探究已知n∈N*,对任意给定的正数c,是否存在x,使得当x∈(x,+∞)时,恒有xn

若n≥5,由2m≥mn+n+1,取m=n.下面证明当n≥5时,2n≥n2+n+1成立.

由① ② 可知,对任意给定的正数c,总存在x,使得当x∈(x,+∞)时,恒有xn

通过以上拓展探究,我们证明了一个一般性的结论:若已知n∈N*,则对任意给定的正数c,总存在x,使得当x∈(x,+∞)时,恒有xn

高考试题是命题专家集体智慧的结晶,每道试题的背景及形成过程都深深根植于教材之中,其解题思路也是在数学思想方法统领下自然形成的,“新而不难,难而不怪”. 因此,高三教学要真正回归教材,大力挖掘其潜在的教育功能;研究高考,尤其是对体现高中数学核心知识及有很好教育价值的高考试题进行深度解析,凸显核心概念的本质,聚焦试题的关键能力特征,挖掘试题所承载的学科核心素养,追寻试题命制的轨迹,领悟命题思想;努力探索高考试题与教材知识之间的最佳契合点,并创造性地使用教材,准确理解和把握数学学科素养,努力探索促进数学核心素养形成和发展的载体、手段和途径,构建以素养立意的课堂教学模式,提高数学教学的质量.