时间序列Landsat 8 OLI数据森林年扰动检测

胡圣元，庞 勇，蒙诗栎，岳彩荣

(1. 西南林业大学林学院，云南昆明 650224；2. 中国林业科学研究院资源信息研究所，北京 100091；3. 国家林业和草原局林业遥感与信息技术重点实验室，北京 100091)

森林变化包括森林突发性变化和时间序列趋势变化[1]。森林扰动是森林突发性变化，是研究者们在森林变化中关注的重点。随着大量中高分辨率卫星遥感数据的免费开放，研究者可利用美国Landsat系列、欧洲Sentinel系列和我国高分系列光学卫星数据开展时间序列森林变化分析研究。目前基于时间序列的森林变化检测方法大致包括3类：（1）基于多时期分类图斑的方法[2]；（2）基于多时序像元级阈值判定的方法[3]；（3）基于长时间序列轨迹分析的方法。基于多时期分类图斑的变化分析方法是通过对不同时期卫星影像进行地物识别和分类，并对分类结果进行比较，从而确定森林变化的发生情况[2]。因此，时间序列数据质量与分类精度都会对变化检测的结果产生较大的影响。基于多时序像元级阈值判定的变化分析方法是通过构建植被指数，计算时间序列中逐个像元的指数曲线，在指数超出阈值时即可检测到森林变化。这类森林变化分析方法包括植被变化追踪算法（Vegetation Change Tracker, VCT）[4]、Hilker等[5]使用的映射反射率变化的时空自适应算法，相比多时期分类图斑的变化检测，该类方法能够在长时间范围内连续观测同一地区的森林覆盖情况，可以得到变化区内更细致的时空变化特征，例如森林在某段时间内经历的成熟-砍伐-恢复-成熟等活动。这类方法的不足是阈值的选取本身会影响变化检测的结果，并且构建的指数会受到辐射差异的影响[1]。基于长时间序列轨迹分析的变化分析方法是通过时间序列光谱轨迹分析来检测森林变化：Hansen等[6]使用的方法是曲线拟合法，即预先确定每种类型森林变化曲线的形状，根据时间序列曲线形状进行变化归类；Land-Trendr方法[7]是分割法，首先将时间序列光谱轨迹分割成一系列直线段以模拟时间轨迹重要特征，再根据分割所得直线段端点提取变化信息；CCDC方法[8]是统计边界法，首先将时间序列曲线分解为趋势、季节变化和噪声，然后对时间序列的统计学边界进行估计，如果某一年的数值超过了估计的边界值则认为有森林变化发生。轨迹分析法相比阈值法，更好地利用了时间序列信息。

VCT算法是多时序森林变化检测方法中的经典方法之一，其构建的IFZ指数（Integrated Forest Z-score，IFZ）简便有效，运算速度较快。Huang等[4]使用VCT算法对美国东部7个州的森林动态变化进行了检测，总体精度达到80%。张连华等[9]通过缨帽变换构建扰动指数（Disturbance Index）以代替IFZ进行变化识别，但仍有检测精度较低的年份。黄春波等[10]在IFZ的基础上引入了NDVI进行加权计算，对三峡大坝附近森林进行变化检测，相比Huang等在美国的结果，漏检率和过检率分别降低到了4.7%和5.3%。VCT算法对森林覆盖变化剧烈的情况较为灵敏，如大规模砍伐、森林火灾等导致的森林扰动等；对森林覆盖变化轻微的情况如择伐、少量病虫害导致的森林扰动以及森林逐渐恢复的检测效果欠佳[4]。同时，有植被覆盖的非森林区（如农田、草地等）的变化过识别会影响森林区域的变化精度。对于农田区，VCT算法利用扰动变化前后数年的信息以排除季相因素导致的伪变化[3]。

通常森林的变化情况在一段时间内相对稳定，较少出现短时间内发生连续扰动，因此VCT算法能较准确地检测出森林发生扰动的年份。然而对于短轮伐期的速生用材林，森林砍伐后的再造林或萌生林相隔时间较短，仅经过两年甚至一年的恢复，IFZ指数便能恢复到正常的森林水平，则VCT算法易判定为森林没有发生扰动，容易出现漏检情况。因此，对IFZ指数进行优化以提高其算法对森林扰动的检测能力，可以减少伪变化同时降低漏检风险。

本研究以高峰林场为研究试验区，在减弱VCT伪变化判读机制的前提下使用了结合NDVI的IFZ指数进行森林扰动的检测，对比使用原始IFZ指数的森林扰动检测结果，新的IFZ指数在保证生产者精度不变的前提下提升了用户精度和总精度。

1 研究区与数据

1.1 研究区概况

以广西高峰林场银岭分场至延河分场为研究区，高峰林场位于南宁市兴宁区北部，坐标范围22°50′～23°4′ N，108°8′～108°32′ E；属湿润的亚热带季风气候，阳光充足，雨量充沛，年平均气温在21.6 ℃左右，年均降水量达1 304.2 mm。森林经营面积8.7万hm2，森林蓄积量570万m3，其中3.3万hm2林地位于南宁市北部丘陵地带，森林覆盖率大于80%。主要树种包括杉木(Cunninghamia lanceolata (Lamb.) Hook.)、马尾松(Pinus massoniana Lamb.)、巨尾桉(Eucalyptus grandis×urophylla)、八角(Illicium verum Hook. f.)、毛竹(Phyllostachys edulis (Carr.) H. de Lehaie)、火力楠(Michelia macclurei Dandy)等[11]。高峰林场拥有大量短轮伐期的速生用材林，森林经营活动频繁，由砍伐产生的森林减少和恢复产生的森林增加较多，呈现出较频繁的森林变化。

1.2 遥感数据获取与数据处理

采用的遥感影像为Landsat8 OLI地表反射率产品，该产品已经过大气校正、正射校正、辐射定标等处理，可通过美国地质调查局地球资源观测与科学中心官方网站下载（http://earthexplorer.usgs.gov）。行列号为125/44的影像完整覆盖高峰林场研究区，研究选取了成像时间为2013年至2019年期间生长季（3—10月）的所有影像数据。根据云的光谱特性及卫星影像的像元质量评估信息等，使用影像合成法利用多期卫星影像的非云像元，生成研究区2013—2019年逐年度的无云影像[12-13]。

1.3 地面数据获取

外业调查于2018年5月11—23日进行。对选取部分研究区的扰动图斑样点进行实地调查，包括研究区边界外部靠近研究区边界的样本在内共采集到实测森林变化情况样本点190个。对非森林区的样本进行系统采样，在研究区及附近以横向30 km、纵向21 km的矩形范围进行了间隔3 km的系统抽样，选取了88个样本点，利用卫星影像对样本点所处或距样本点较近的扰动图斑进行目视判读，获取扰动信息。共采用278个样本点对扰动检测结果加以验证。实地调查样本点及系统抽样目视判读样本点空间分布如图1所示。

图 1 外业调查样本点空间分布图Fig. 1 Distribution of field plots

2 基于综合森林指数检测森林扰动

2.1 VCT算法介绍

VCT算法的基本原理是在影像中自动提取森林样本，以此森林样本作为参照，计算每个像元与纯净森林像元的相似性程度，即森林指数（FZ），再结合多波段或者多指数的FZ形成综合森林指数（IFZ）。IFZ可作为每个像元是否为森林像元的判断依据，根据每个像元IFZ指数的变化情况来判断该像元在时间序列中所处的时间年份是否发生了森林扰动[3]。

由森林像元的光谱曲线特征可以看出，其在红光波段的反射率较低，当森林样本达到一定数量时，就会在红光波段反射率直方图的低值区域形成峰值，即森林峰值。通过提取该峰值区域的像元，同时对水体和阴影进行掩膜处理，即可得到纯净的森林样本像元[14]。对于整景Landsat影像，不同地区的森林可能由于物种类型、群落结构、地形等因素导致的光谱差异，呈现略有差别的光学特征，若对全景影像采用直方图森林峰值法提取森林样本，会导致提取到的森林样本较为单一[15]，因此可采用一定尺寸窗口将影像划分为若干区块，每个区块单独进行直方图森林峰值的提取。设置窗口时不宜过小，否则可能会因窗口未包含森林样本而将农田等其他地物的峰值作为样本提取，从而导致森林样本不准确。在本研究中采用400×400像元窗口大小。

森林指数是基于像元统计特征的指数，它表示了每个像元与纯净森林像元的相似程度。FZ与IFZ的计算公式如下：

其中NB为参与运算的波段数目，bp为每一个像元在某一波段上的值，为i波段上森林样本像元值的均值，SDi为i波段上森林样本像元值的标准差。在使用单波段进行计算时（NB=1），IFZ等同于森林指数FZ；使用多个波段时（NB＞1）即为综合各波段的FZ值得到整合值IFZ。

由公式（1）可知，像元的IFZ值越低，其与纯净森林样本越相似，越有可能是森林，反之则为非森林。排除水体和阴影对IFZ变化的影响后，每个像元IFZ值的变化情况可用于检测发生森林扰动的时间点。若像元点在某年的IFZ值与其前一年相比有显著的提升，那么它就有可能是一个由森林向非森林转变的变化（扰动），若像元点在某年的IFZ值与其前一年相比有显著的降低，则可能是从非森林转变到森林。因此设置衡量IFZ变化量的阈值d1作为判断森林扰动的依据，若前后年份IFZ的差值大于d1，则认为极有可能发生扰动。但只有差值并不能确定发生了森林扰动，因为非森林像元的IFZ波动同样可以造成较大的IFZ差值。因此，设置一个阈值d2用于界定变化前后地物类型，只有当潜在变化点的前一时刻的IFZ值低于d2时，这样的变化才是一个由森林向非森林转变的变化。

为了提高IFZ对森林与非森林植被的区分度，以减少检测到的伪变化、降低过检测率、提高用户精度，本研究采用将NDVI与原始波段加权结合的方式，从而得到更好的森林扰动检测结果。研究流程如图2所示。

图 2 综合森林指数检测森林扰动流程Fig. 2 Workflow of forest disturbance detection using forest z-scores

2.2 融合NDVI的IFZ森林指数

在已有的使用VCT算法的森林变化检测方法中，参与运算IFZ指数的波段并不相同，Huang等人对Landsat 5 TM影像选用了红波段和两个短波红外波段[3]；Pang等使用Landsat 7 ETM+影像时选取了蓝、绿、红、近红外和两个短波红外共6个波段[16]。但有研究表明，虽然森林冠层在近红外光谱区间的反射率很高，但是非森林的地表根据其覆盖情况不同，在近红外光谱区间的反射率或高或低，从而导致在这个波段上发生的反射率在某一特定方向上的变化并不一定代表森林覆盖发生变化，因此不宜使用近红外波段作为IFZ指数的计算因子[4]。此外，蓝、绿、红波段之间有着显著的相关性[17]，因此也不宜同时使用这3个波段。植被指数也可以参与IFZ的计算。部分农田的光谱与森林相近，其IFZ值也相对较低，有时可以和IFZ值较高的森林相当，因此农田等非森林植被会对森林扰动检测产生干扰，在高峰林场这样变化频繁的区域，部分森林扰动产生的IFZ变化与农田的IFZ变化更难以区分；将NDVI作为计算因子之一参与到IFZ的运算中，所得到的新的指数NIFZ，能较好地减弱农田对森林扰动检测的影响[10]。

2.3 IFZ的波段加权

由IFZ的公式可知，像元的IFZ值是参与计算的每个波段FZ值的平均。在引入了NDVI作为新波段参与运算后，由于植被指数波段的取值范围与反射率波段的取值范围不同，例如可见光波段的反射率实际取值范围大部分集中在0.2以下，NDVI值则较少出现低于-0.4的情况，因此不同波段的FZ存在取值范围不等的问题。为了统一各波段FZ值的取值范围，需将各波段FZ结果按比例缩放到同一尺度。将参与计算的波段乘以同一个放大系数，从而将各个波段FZ换算成具有相同权重的指数因子。因此，本研究将参与运算的首个波段作为基准，以各波段FZ值的均值作为确定缩放比例的参考，即为NIFZ：

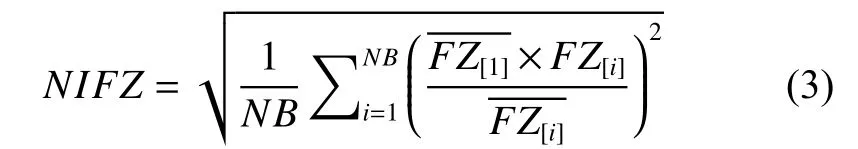
2.4 计算流程与验证方法

使用合成影像的蓝、红、近红外和两个短波红外波段进行计算和分析。首先使用NDVI与近红外（845～885 nm）、蓝波段（450～515 nm）对水体和阴影进行阈值法掩膜；接下来对影像的红波段（630～680 nm）以400×400像元大小为窗口遍历影像，利用直方图的森林峰值提取森林样本，得到每一影像的森林样本，并以此样本计算NIFZ，以及由此衍生的NIFZ2和NIFZ3。最后，计算红、短波红外1（1 560～1 660 nm）和短波红外2（2 100～2 300 nm）3波段的IFZ指数进行对照。

为了对比各指数在区分森林像元和非森林植被像元的表现，分别选取了不同年份、不同位置的若干森林区和非森林（农田为主）像元的4种指数值进行了对比。从图3可以看出森林像元的NIFZ2与NIFZ3值的分布比IFZ和NIFZ更为集中，而就逐年取值分布来看，NIFZ与NIFZ2的森林与非森林像元的区分度更大。4种指数在森林与非森林之间都存在着重叠区间，相比之下NIFZ2的重叠区间更小。从曲线形态来看（图4），4种指数的曲线形状是相近的，都能够反映森林扰动变化特征。此外，根据4种指数逐年取值分布情况可以选定森林像元与非森林像元指数值的区分阈值d2，进行后续的森林扰动检测的运算。在此，对IFZ、NIFZ、NIFZ2和NIFZ3，d2的值分别取4.5、3.5、2.5和2.3。

在分别利用各指数得到对应的森林扰动检测结果后，利用验证点扰动信息与对应位置的检测信息进行对比，逐年记录检测情况与实际情况，统计各指数检测结果的漏检测率、过检测率和总精度，以进行各指数的精度评价。

图 3 4种综合森林指数在森林和农田的取值区间对比，末尾的f与n分别表示森林和农作物Fig. 3 Comparison of value ranges of 4 z-scores in forest(-f) and crop(-n) areas

3 结果与讨论

采用IFZ、NIFZ、NIFZ2和NIFZ3作为反映森林扰动指数应用于VCT算法中，在不使用前后年份进行验证的情况下得出森林扰动检测的结果，并使用外业调查数据结合卫星影像来进行二者的精度检验。其中NIFZ2得到的结果如图5所示。由不同指数扰动检测结果对比图（图6）来看，4个指数的表现较为相似，但NIFZ与NIFZ2的检测结果相比IFZ的结果减少了很多细碎的图斑。总体而言，NIFZ2的检测结果减少了大量主要类型为2015年森林扰动的孤立像元，从检测结果图上看是效果最好的指数。

最终，使用采集和抽样的验证点对4种指数的检测结果进行验证，各指数的检测精度如表1所示。总体情况显示，NIFZ2的精度最优，总精度达79.2%，NIFZ其次，为77.4%；而从年度情况来看，2014年4个指数的用户精度都比较低，而2015年NIFZ2的用户精度获得了较大提升，其余3个指数的用户精度虽比2014年有所提升但仍然不理想。精度较低主要是由于2013年和2014年的影像中残存的云像元对检测结果有一定影响；3种指数中NIFZ3的精度最低，说明对不同年份的森林指数结果进行加权比较并不能消除不同年份之间的差异，同时可能还会对森林扰动的识别带来负面的影响，这可能是由于尽管不同年份之间森林像元指数值存在差异，但利用森林峰值提取森林样本时，不同年份的影像提取到的森林峰值的反射率值较为接近，所以被选为森林样本的像元的指数值的差异在不同年份之间并不大，因此对不同年份加权并没有令NIFZ3在相同地物上不同年份间的表现趋近相同。

图 4 4种综合森林指数在扰动区的时间序列特征Fig. 4 Curves of the four z-scores in a forest disturbance area

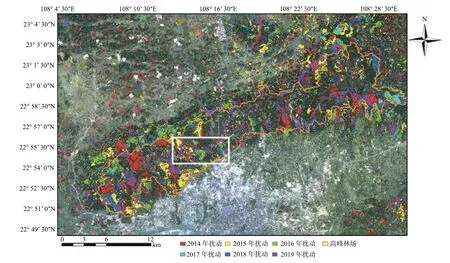
图 5 应用NIFZ2的VCT森林扰动检测Fig. 5 VCT forest disturbance detection using NIFZ2

图 6 应用4种综合森林指数的VCT森林扰动检测局部对比，对应图5白框Fig. 6 Comparison of VCT forest disturbance detection results of four z-scores, located in the white box of Fig. 5

表 1 4种综合森林指数变化检测的精度对比Table 1 Comparisons of change detection accuracy using four different z-scores

高峰林场的验证结果表明，采用NDVI的3个指数所得到的森林扰动变化检测结果的精度均好于采用原始影像光学波段的IFZ的扰动检测结果。相比IFZ的结果，3种使用NDVI并加权的指数的用户精度得到了显著提升，而生产者精度则有小幅度的降低。由于Landsat8地表反射率产品未经过地形校正，处于向阳坡面的森林，其指数取值会比背阳面更高，更加接近农作物等非森林植被的指数；此外，不同质的森林由于树种、密度、郁闭度等差异，也会影响森林指数值。这些都是利用阈值判断的森林变化检测方法的不确定因素，加权融合NDVI与IFZ的方法增加了森林与非森林在森林指数上的区分度，间接降低了这些不确定因素的影响，从而提高了森林扰动检测的精度。其他遥感衍生的植被指数例如增强型植被指数（EVI）和差值植被指数（DVI）也能够反映森林覆盖变化相关的信息，但对于上述指数是否适用于提高IFZ的检测精度有待进一步验证；此外，经过穗帽变换所得到的波段，同样含有森林变化的信息[18]，也有着与IFZ相结合的可能性。

4 结论

通过将植被指数引入时间序列的综合森林指数，提供了植被变化追踪算法在森林扰动频繁区域的适应性，主要结论如下：（1）在NDVI与IFZ的结合方式中，采用森林样本FZ均值加权的NIFZ2指数的检测精度最优，其精度比IFZ提升了12%；（2）使用年度森林样本FZ均值对不同年份指数进行加权并不能有效提高扰动检测的精度；（3）通过在IFZ中加入NDVI因子，使算法的误检率大大降低，平衡了快速变化区域内的漏检与误检的问题。