双线圈接地电阻测量法的优化

战 凯，陈 星

（大连理工大学，辽宁大连 116024）

0 引言

接地电阻是电力系统接地的重要技术指标，准确获得电力系统电阻值是保证电力系统安全运行的前提[1]。目前，国内接地电阻测试仪器普遍存在精度低、测量过程复杂、抗干扰能力差等问题[2-3]。本文针对传统的双线圈接地电阻测量方法从驱动信号、线圈圈数、输入电压、输入频率等方面进行优化。研制出了精度高、抗干扰能力强的接地电阻测量装置。简化了测量工作人员的操作，并减少了接地电阻测量系统的测量误差。

1 测量原理

电磁感应现象是指在变化磁通量的导体内会产生电动势，该电动势称为感应电动势，如果导体闭成一个回路，电子会因该电动势产生流动，生成感应电流[4]。测量装置的原理如图1所示。

其中，Nv为缠绕在特定纳米晶材料制成的磁环上的输入线圈的圈数，Ni为缠绕在特定纳米晶材料制成的磁环上的输出线圈的圈数。测量时，输入电压线圈产生一个已知的恒定低频交流电压U，通过输入线圈和被测电阻的电磁感应以及被测电阻和输出线圈的电磁感应，可以在输出线圈上产生一个输出电压u，且u和Rx应为反比关系，通过大量的实验，找出输出电压和被测电阻的关系，即可计算出接地电阻Rx:

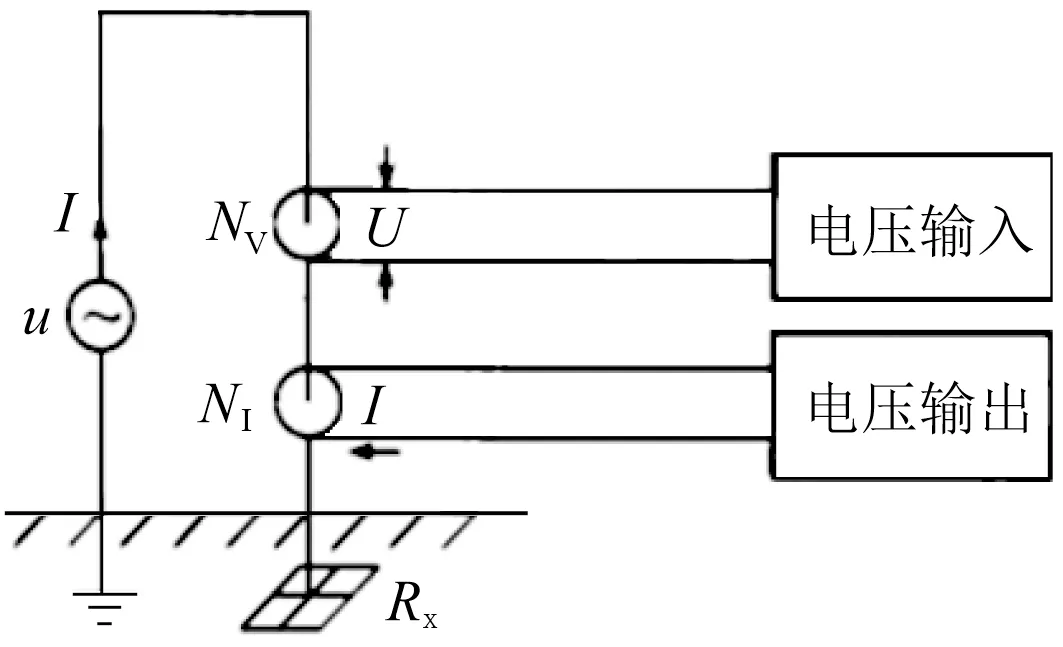
图1 双线圈接地电阻测量原理图

式中：a、b、c为比例系数。

2 测量仪器及材料

实验所用的电感材料是纳米晶，纳米晶的电导被量子化，并随着纳米晶丝直径的减小出现电导台阶、非线性的曲线及电导振荡等其他材料所不具有的电导特性[5]。纳米晶材料是目前导磁率最高的材料之一，具有高饱和磁感应强度，低铁损等特性[6]。

输入信号主要由信号源发生器进行产生，频率在1～10 000 Hz之间可调，幅值在1～20 V之间可调，可满足输入的需求。

输出的信号在示波器上进行显示，并将波形导入计算机中，用Matlab 对输出的波形进行滤波，去掉环境的干扰，同时可以进行频率和幅值的测量，便于实验的观察与记录。

3 计算结果

根据电磁感应测量接地电阻的原理，影响测量精度的因素主要是输入线圈圈数、输出线圈圈数以及输入信号，而输入信号由波形、幅值、频率几个因素决定。故实验采用控制变量的方法，分别从输入线圈和输出线圈圈数、输入信号的波形、频率、幅值进行比较，最终找到最优的参数。

3.1 正弦波和方波输出比较

在传统仪器中，正弦信号一般由文氏振荡器产生，其电压、频率稳定性差，不易改变频率[7]。当前也可利用单片机的可编程定时器产生PWM 信号后将PWM 转换成正弦波，但这对电路的要求很高，实现也相对复杂[8]。因此考虑用简单的方波代替复杂的正弦波。

使用市面上常用的传感器，将目标正弦波形和方波的输入输出进行了比较，采用了控制变量的方法，比较了不同输入频率（2 000 Hz、500 Hz）和不同输入电压（5 V、15 V）下方波和正弦波误差，通过示波器进行观察，发现正弦波和方波在输入相同的情况下，输出的数据差距不大，误差可以忽略不计，如表1、表2 所示。方波相比于正弦波简单，易于观察，波形失真小。故采用方波信号来代替正弦波信号。

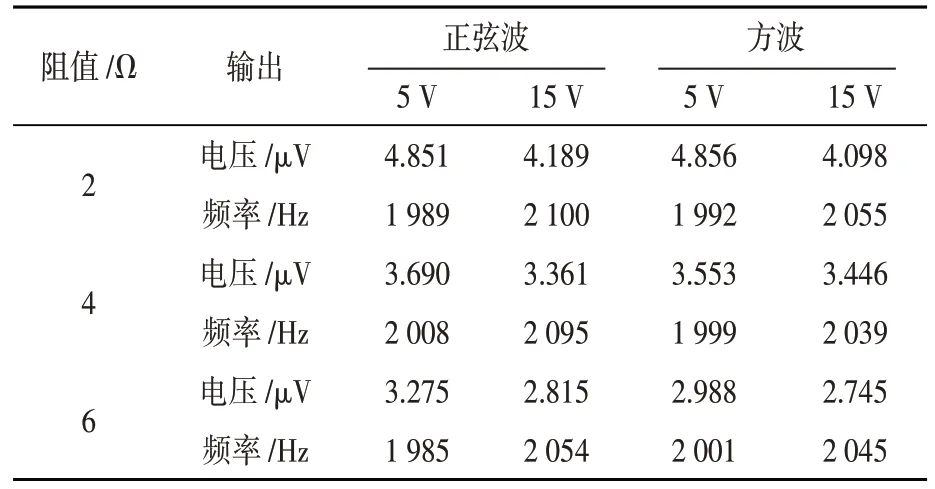
表1 2 000 Hz正弦波和方波输出比较

表2 500 Hz正弦波和方波输出比较

3.2 输入线圈和输出线圈圈数对结果的影响

当线圈圈数少于10圈时，由于通电线圈的电阻较小，会造成短路，因此本实验输入和输出线圈的圈数都大于10 圈，为了安全起见，从15圈开始实验。实验采用了控制变量的方法，输入的电压为5 V，频率为2 000 Hz，测量电阻选择1～10 Ω，首先改变输入和输出线圈的比例进行实验，如表3所示。

表3 不同输入输出线圈比例平均误差

由表3可知，输入线圈为15圈，输出线圈为30圈时，即输入线圈和输出线圈的圈数比在1∶2 时，测量的误差最小，运用Matlab做出拟合函数为，如图2所示。

后续实验继续采用输入电压为5 V，输入频率为2 000 Hz，输入线圈圈数和输出线圈圈数为1∶2的比例进行实验，如表4所示。

图2 输入线圈15圈输出线圈30圈电阻和电压的拟合函数

表4 输入输出线圈1比2不同线圈圈数误差

由表4 可知，随着输入线圈和输出线圈圈数的增多，测量误差逐渐减小，当输入线圈为45 圈，输出线圈为90 圈时，测量的误差最小，随后随着输入线圈和输出线圈的增多，误差逐渐增大。如图3所示，运用Matlab做出拟合函数为：

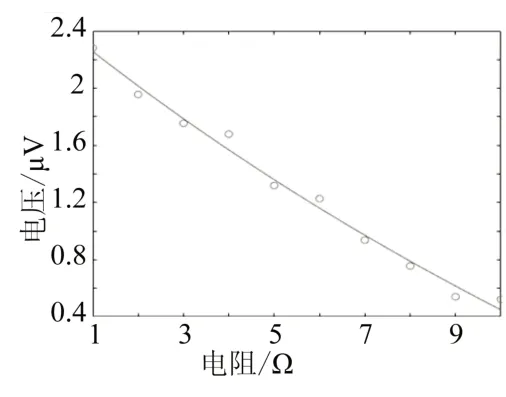
图3 输入线圈45圈输出线圈90圈电阻和电压的拟合函数

图4 输入线圈41圈输出线圈90圈电阻和电压的拟合函数

选择输出线圈为90圈，改变输出线圈的圈数，继续做实验。由表5 可知，当输入线圈的圈数为41 圈时误差最小，故选择输入线圈为41 圈，如图4 所示，运用Matlab 做出拟合函数为：

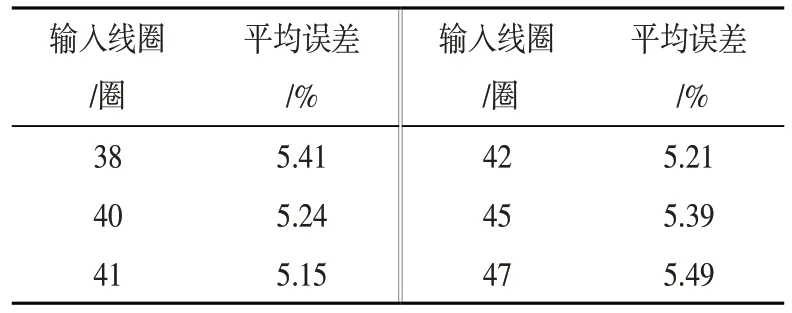
表5 输出线圈90圈不同输入线圈平均误差

选择输入线圈为41 圈，改变输出线圈的圈数，继续实验，找出输出线圈的最优的圈数。由表6的实验可知，输出线圈为85圈时，测量误差最小，故选择输入线圈为41圈，输出线圈为85圈。如图5所示，运用Matlab做出拟合函数为：

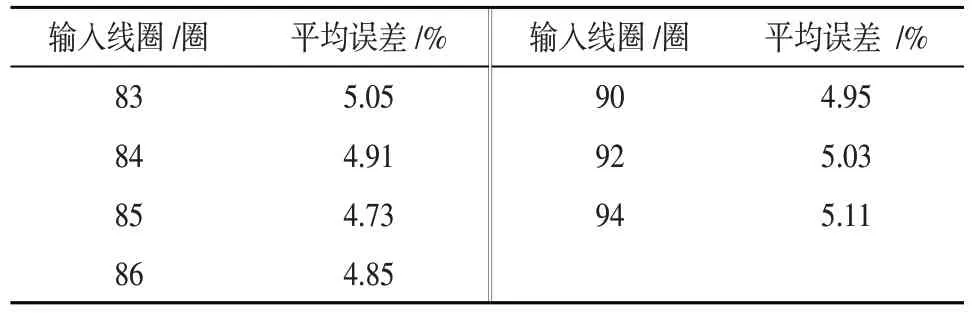
表6 输入线圈为41圈不同输出线圈平均误差

图5 输入线圈41圈输出线圈85圈电阻和电压的拟合函数

图6 频率500 Hz时电阻和电压的拟合函数

3.3 输入频率对测量结果的影响

由上述实验可知，当输入线圈圈数为41，输出线圈圈数为85时，测量误差最小，为了探究输入信号的频率对测量结果的影响，选用输入电压为5 V，输入线圈圈数41，输出线圈圈数85进行实验。

表7 100～2 000 Hz频率不同频率的平均误差

由表7可知，频率在500 Hz时，平均误差最小，如图6所示，运用Matlab做出拟合函数为

继续在100～500 Hz和500～1 000 Hz之间实验，如表8和表9所示。由表8和表9可知，频率在600 Hz时，平均误差最小，如图7所示，运用Matlab做出拟合函数为：

表8 100～500 Hz不同频率的平均误差

表9 500～1 000 Hz不同频率的平均误差

3.4 输入幅值对测量结果的影响

由上述实验可知，当输入线圈圈数为41，输出线圈圈数为85时，输入频率为600 Hz时，测量误差最小，为了探究输入信号的幅值对测量结果的影响，选用输入频率为600 Hz，输入线圈圈数41，输出线圈圈数85进行实验。

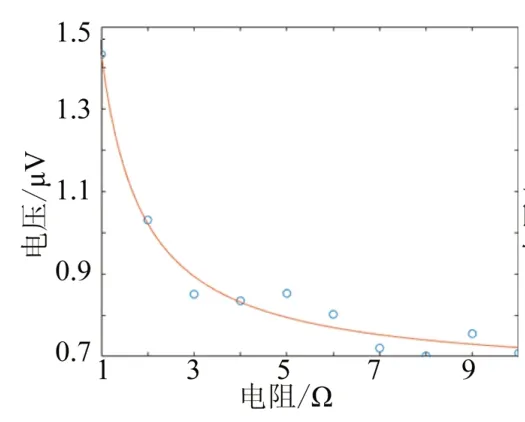
图7 频率600 Hz时电阻和电压的拟合函数

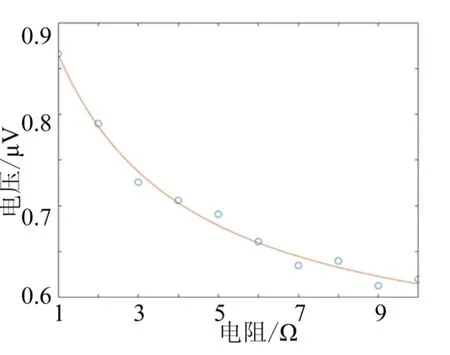
图8 电压7 V时电阻和电压的拟合函数

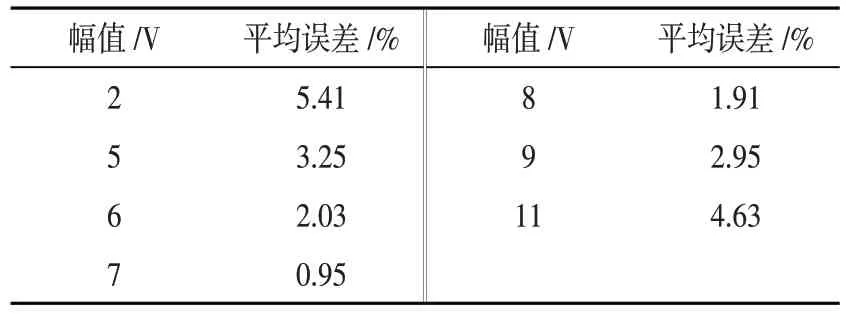
表10 不同电压的平均误差

由表10 可知，电压在7 V 时，平均误差最小，如图8 所示，运用Matlab做出拟合函数为：

4 结束语

本文对传统的双线圈的电阻测量的传感器进行了优化，从一定程度上解决了该传感器测量精度不高的问题，为在线电阻测量提供了一定的基础。当输入线圈的圈数是41圈，输出线圈的圈数是85圈，输入频率为600 Hz，输入电压为7 V时，测量的误差最小，为0.95%。实验室测量结果表明，优化后的测量方法测量精度高，具有较高的实用价值[4]。测量电阻的计算公式可简化为

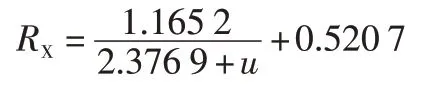
本文从双线圈接地电阻测量法等方面进行了优化，但是由于制备工艺的原因，纳米晶材料制成的磁环的相关性能参数有一定的离散性，测量仍旧存在一定的误差，为了进行快速标定，可多次测量取平均值，并且将传感器套上外壳，以隔绝外界干扰。