一种桥式起重机防摇控制实验平台设计与分析*

2020-11-27邱光繁李汶杰邱炯智黄晓存张京玲王天雷

机电工程技术 2020年10期

邱光繁，李汶杰，邱炯智，黄晓存，张京玲，王天雷※

（1.江门市蒙德电气股份有限公司，广东江门 529000，2.五邑大学智能制造学部，广东江门 529000；3.恩平市奥达电子科技有限公司，广东江门 529030）

0 引言

在各领域的工程建设、生产车间，桥式起重机被广泛应用于搬运重物，对其控制主要是将货物安全、快速、准确地搬到目标位置。但由于工作环境复杂，人工操作不可避免地造成被吊物摇摆，加速机械磨损，增加吊物转运时间，效率较低，且事故时有发生。图1所示为常见的桥式起重机。

基于上述原因，多种防摇控制策略已开发并用于桥式起重机的防摇系统，有效地降低了吊物运转过程中的摆动，使起重机运行更加高效、安全[1]。

对防摇系统基本要求：被吊物应能精确定位；运行过程中摆角尽量小，在到达目标位置前吊物应停止摇摆。目前，防摇摆控制技术可分为机械防摇摆和电子防摇摆。电子式防摇是通过各种传感器和检测元件将检测到的信息，如吊物的摆角、吊车运行速度、吊车的位移和吊物起升高度等，传送至控制系统，系统处理后将最佳的控制参数定量。通过调节吊车速度，提供最佳策略控制起重机的运行，减小吊具及吊物的摆角[2]。

图1 桥式起重机

1 防摇实验平台

1.1 基本要求

设计一种防摇控制实验平台为教学、科研服务，即对各种防摆控制算法在Matlab/Simulink 实现后，进一步在该平台上进行实验测试，以便为其实际应用提供可靠依据。按相似原理设计，即实验平台基本结构参考实际桥式起重机，基本尺寸按比例缩小。设计的实验平台如图2所示。

图2 桥式起重机防摇控制实验平台

1.2 工作过程

如图3 所示，工作过程为：通过计算机的控制界面发出指令实现控制卡对电机控制，包括电机正反转、运行距离/速度/时间/加速度大小和加速时间，电机带动滚珠丝杠驱动小车移动，在移动过程中被吊物产生的摆角可实时测出，并将信号反馈，经运动控制卡输入到控制界面，进而达到实时控制小车的运动，从而达到防摇的目的。系统控制维数说明：一维控制为仅控制小车沿X 方向运动；二维控制是同时控制小车移动和升降装置升降负载；三维控制为同时控制小车沿X、Y方向移动以及升降装置升降负载。

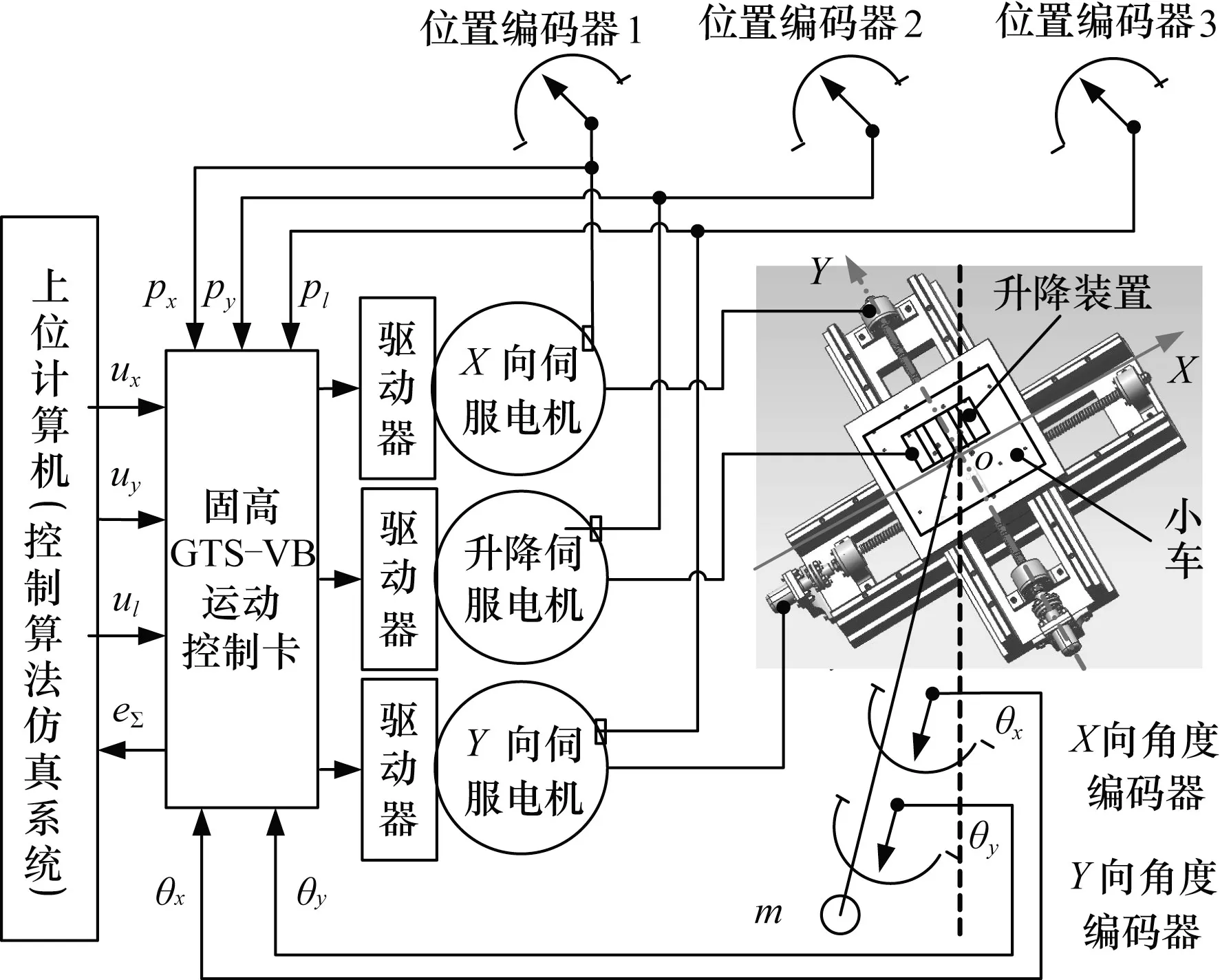
图3 实验平台结构示意图

1.3 实验平台主要硬件

平台采用固高GTS-VB运动控制卡，该控制卡是以PCI总线为基础、以ASIC 为核心，可实现4 轴伺服电机和步进电机的多轴点位控制，另带有编码器位置检测等复杂功能；选用MR-E-100A 伺服放大器，其具有保护电路、正弦波PWM 控制、电流控制系统等功能，可以使整套系统得到更好地控制；摆角测量装置是通过旋转编码器和机械结构共同组成，具有安装方便、测量精度高等特点；采用三菱伺服电机和滚珠丝杆副能实现运动状态的高精控制，满足实验装置运动要求。

1.4 系统软件

防摇实验系统的控制算法输出的控制量为一个数字量。因此，需要调用的运动控制方法函数要能够完成数模转换输出，使被控对象进行相应地运动。本设计中用到的运动控制方法函数原型为：gts.mc.GT_SetDac（short dac, short *pValue,short count），其中，dac参数为运动控制卡所控制的对象的起始轴号，pValue参数为输出的电压（-32 768对应-10 V，32 767对应+10 V），count参数为所要控制的轴的数量。综合对桥式吊车负载防摆系统的介绍和给出的上位机软件基本功能分析，经过细化后，得到如图4所示的上位机软件详细功能框图。

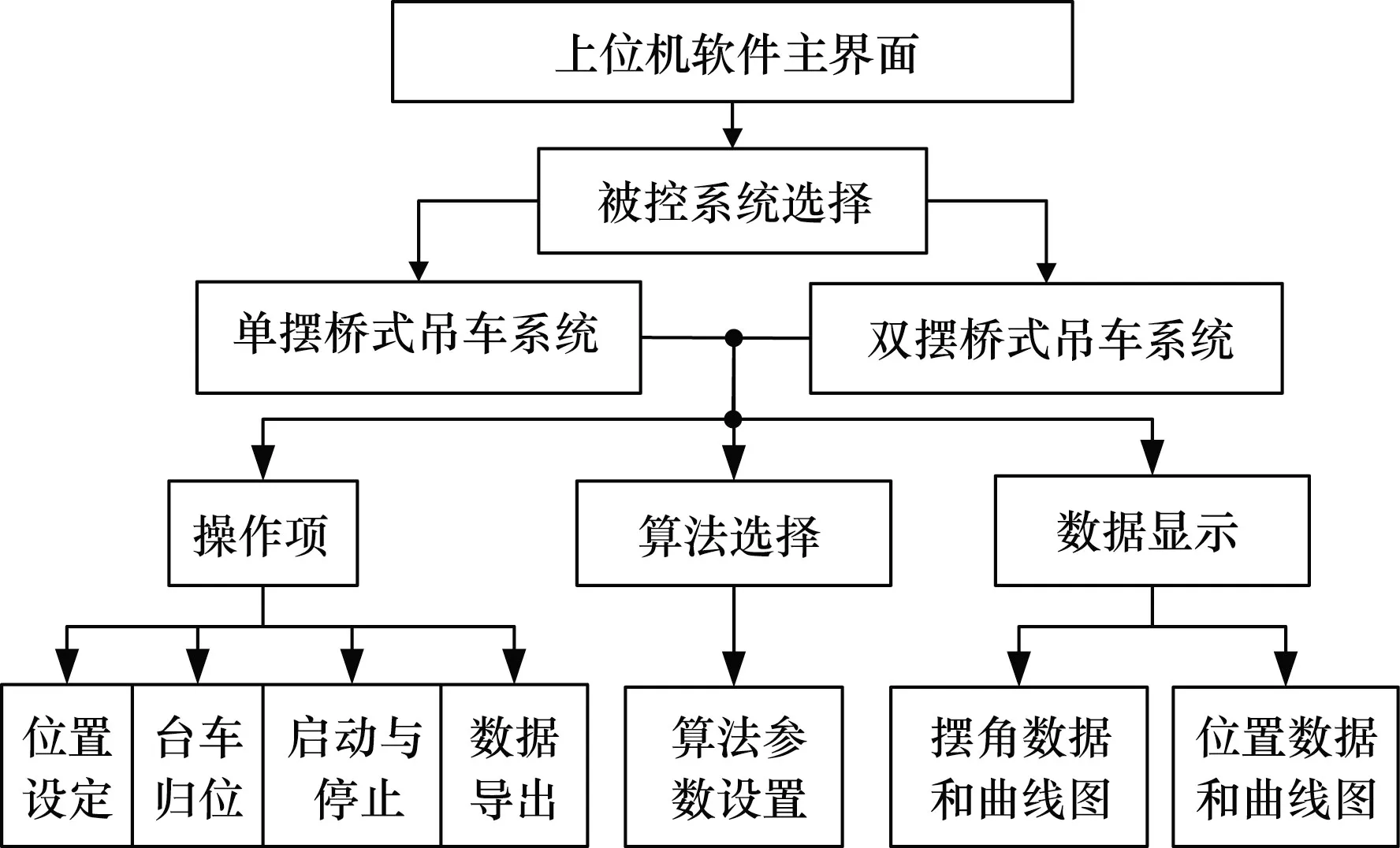
图4 上位机软件详细功能框图

1.5 仿真实例

二维桥式起重机防摇系统的算法仿真动力学模型[3]如图5 所示。小车质量为M，水平方向的牵引力F 及阻力f，阻力系数为μ；负载质量为m，绳索长度为l。忽略绳索的质量、绳的弹性形变、空气阻力、风力、吊绳与台车连接处的摩擦力等。建立坐标系，设负载与台车的坐标分别为（xm,ym），（xM,yM），负载摆角为θ、绳长为l、水平方向位移为x。将仿真参数值输入该系统，进行PID 控制、模糊控制和模糊PID 控制对比仿真分析，图6所示为所得仿真曲线。

图5 桥式起重机二维力学模型

图6 仿真对比分析结果在上位机的显示

2 平台机架的有限元分析

机架是支撑小车、负载（起吊物）和电机等的平台，对其设计要求为：（1）足够的强度；（2）良好的动力学特性[4]。因而作以下分析。

在Solidwork 中建立机架三维模型，并进行一定的简化，导入ANSYS Workbench 中对进行有限元分析，采用六面体自由网格划分。机架材料为6061 铝合金型材，弹性模量E=69 GPa，泊松比μ=0.33，密度ρ=2.71 g/cm3，最小屈服极限55.2 MPa；极限抗拉强度124 MPa；弯曲极限强度228 MPa。施加载荷为小车质量5 kg，重物质量10 kg，用Mass21质量单元代替小车和重物的质量添加在轨道中心节点位置，方向Z 轴负向，大小为625 N。有限元模型、网格模型、载荷及边界约束如图7所示。机架与地面接触处进行固定约束，即6个自由度均进行约束。采用Solid187单元进行仿真。

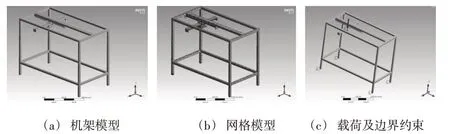
图7 网格模型、载荷及边界约束

2.1 静力学分析

如图8（a）所示，最大应力为31.70 MPa，小于屈服极限，满足要求。图8（b）所示为位移云图，在主梁中部最大位移量为0.117 mm，基本满足设计要求。

图8 静力学分析

2.2 模态分析

模态分析是基于多自由度系统以某一固有频率振动时所呈现的振动形态称为模态，此时系统各点位移存在一定比例关系，称为固有振型。不论何种阻尼情况，机械结构对外力的响应都可表示为由固有频率、阻尼比和振型等模态参数组成的各阶振型模态的叠加。系统运动微分方程为：

式中：[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；分别为系统的加速度、速度和位移；{F}为载荷向量。

求解系统的固有频率和固有振型时，由于结构的阻尼对其模态频率及振型的影响很小，可忽略。

系统的自由振动方程可简化为：

式中：{φ}为位移矢量的幅值；ω为角频率。

将式（3）代入式（2）得：

式（4）在任何时刻t均成立，除去含t的项得：

由线性代数方程组有非零解的充分必要条件：

如平台机架动力学特性不理想，其机架部分可能产生振动，影响负载精准定位的实现和摆角的降低[5]。本文采用模态分析方法，具体步骤如图9所示。

图9 模态分析流程框图

本次分析采用的是子空间法，分析前6 阶模态如图10 所示，对应的固有频率与振型描述如表1所示。

2.3 激励源分析

图10 平台机架前6阶模态振型

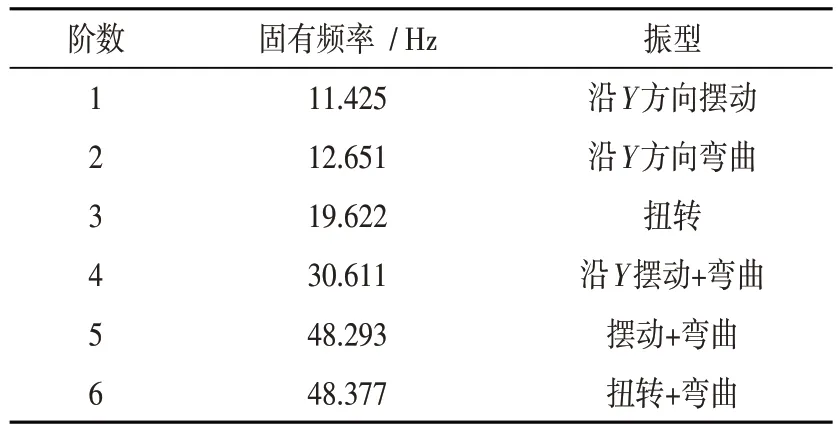
表1 前6阶固有频率

防摇实验平台工作时，伺服电机驱动滚珠丝杆带动小车沿滚动导轨移动，由于伺服电机转子不可避免地存在质心偏离，电机运行时所产生的振动激励可能影响平台工作性能。

以伺服电机安装平台机架为研究对象，对其动态特性开展研究，分析最大响应点随激励频率的变化规律，确定工装平台的振动敏感区域[6]。为其结构的改进与优化提供理论依据。

激励源分析如下。

（1）设计的伺服电机在进行实验测试时转速为1 000 ～2 000 r/min，对应旋转产生的激励频率为16.67～33.34 Hz，如表2所示。

表2 机架2个激励源数据

（2）桥式起重机系统是一种强耦合、非线性的吊摆系统[7]，为使防摇系统实现快速定位和控制移动过程中负载摆角最小[8]，采用各种控制策略和算法均要求频繁变换伺服电机工作时输出转矩，与之对应的角加速度变换周期为50～100 ms，所生产的扭转激励可能导致机架产生颤抖，影响小车准确定位和对负载绳索摆角的控制。加速度变换周期及对应的变换频率如表2所示。