预紧力作用下螺栓的有限元分析
2020-11-27李春光李万里钱红飚杜庆升徐金帅
李春光,李万里,钱红飚,杜庆升,徐金帅
(1.大连益利亚工程机械有限公司,辽宁 大连116025;2.大连理工大学工程力学系,辽宁大连116024;3.大连益网科技有限公司,辽宁 大连116025)
0 引言
在工程实践当中,螺栓作为最基础连接标准件之一,因其具有连接方便、可靠等优点被广泛应用于航天、航空、造船、汽车、吊装以及各种工程结构当中,因此螺栓选型和设计计算的合理性就显得尤为重要。目前对螺栓的设计计算还是以理论计算为主,但是对于复杂结构中的螺栓,理论校核异常繁琐,并且具有一定的局限性。
本文提出一种适用于螺栓的有限元分析方法,通过建立相应的有限元模型,用接触分析法计算两块连接板在额定外载荷作用下,螺栓承受不同预紧力时的拉伸应力,并将计算结果并与理论计算进行对比。
1 螺栓预紧连接的理论分析
螺栓在承受预紧力和轴向工作拉力后由于螺栓与被连接件不可避免的发生弹性变形,导致螺栓所承受的总拉力并不等于预紧力与工作拉力之和。因此,可以通过分析螺栓受力和变形的关系来最终确定螺栓的承载力。螺栓的受力变形图如图1 所示。
根据螺栓的受力变形图确定螺栓和被连接件的受力变形关系,并采用线图的方式来表示,螺栓受力的变形线图[1]如图2 所示。

图1 螺栓受力变形图
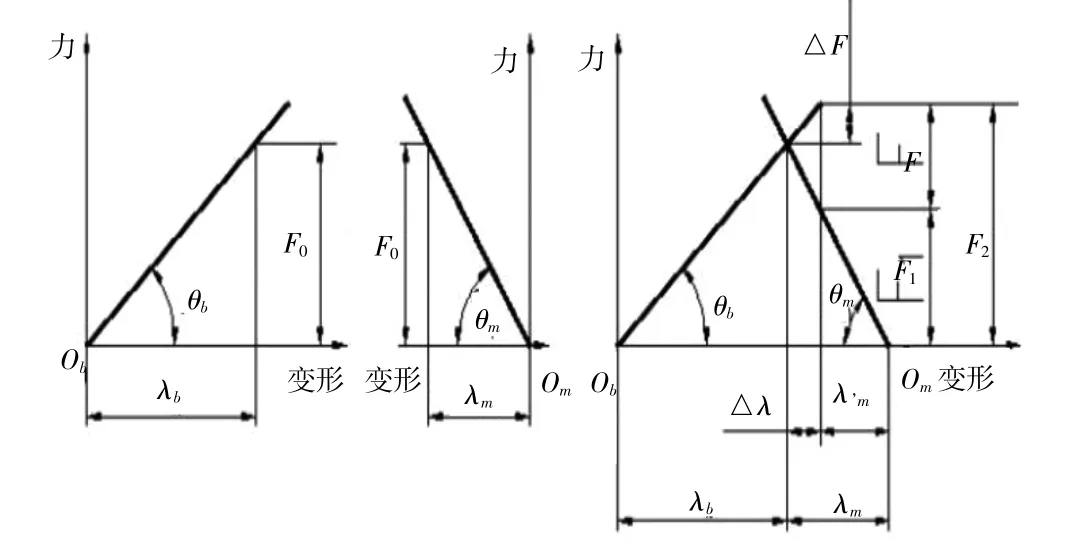
图2 螺栓受力变形线图
根据螺栓的受力变形线图可以清晰的得出预紧力F0与残余预紧力F1、总拉力F2、工作拉力F 几者之间的关系。由此可得出:

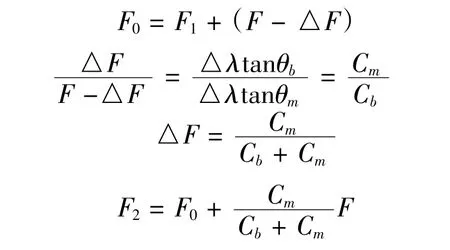
Cm、Cb分别表示螺栓和被连接件之间的刚度且它们均为定值。根据机械设计手册[2]可知受轴向载荷的螺栓连接的相对刚度系数见表1。

表1 螺栓与连接件间的相对刚度系[2]
螺栓因承受预紧力和额定外载荷产生的拉伸应力[1][σ]可表示为:

2 螺栓连接有限元分析
2.1 分析实例
本文选取一个典型的算例进行计算。选用性能等级8.8S 级的M16 螺栓将两块连接板进行紧固,其中上连接板承受5 000 N 的额定外载荷,校核时分别对螺栓施加10 000 N、30 000 N、50 000 N、70 000 N的预紧力,通过有限元的方式分别求出螺栓的拉伸应力并与理论计算进行对照分析。
2.2 有限元模型的约束与载荷设定[3]
此次采用实体单元进行建模,并用Ansys Workbench 软件对螺栓连接结构进行接触分析。
螺栓与螺母连接处加载螺栓的预紧力,上连接板加载5 000 N 额定外载荷,结构计算的有限元模型与载荷加载如图3 所示。

图3 螺栓连接结构的有限元模型与载荷图
2.3 有限元模型的网格划分
采用六面体网格[3],如图4 所示,网格大小为5.0 mm,单元总数7 069 个,节点总数为27 356 个。
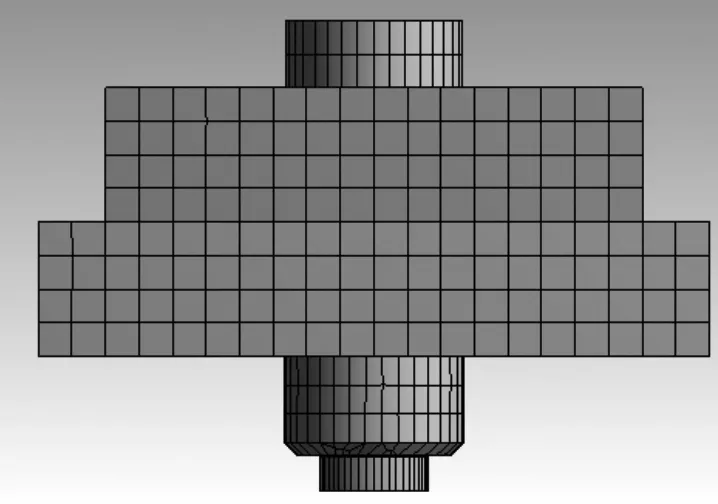
图4 螺栓连接结构的有限元网格图
2.4 接触分析[4]的基础设定
2.4.1 载荷步的选定
接触分析[4]是非线性的问题,一般的默认设置是无法满足计算需求。此次设定两个载荷步,第一载荷步施加螺栓预紧力,第二个载荷步用来锁定螺栓预紧力,然后正常施加外载荷。
为了提高计算的收敛性,将第二个载荷步分解若干个求解点,载荷步2 详细的设置方式可按照图5所示去设置。

图5 载荷步的设置
2.4.2 接触设定与算法选择
螺栓与螺母连接面的接触设置为bonded,设置算法为MPC。因为此种方法常常用于绑定与不分离类型的约束;对于其它零件的接触类型可选择Frictional,并设定相应的摩擦因数,设置算法为Augmented Lagrange,这种Lagrange 乘子法通过增加一个附加自由度(接触压力)来满足不穿透条件,不涉及接触刚度和穿透。
2.5 计算结果(预紧力70 000 N)
计算结果是在预紧力为70 000 N,额定外载荷5 000 N 的计算工况下对螺栓的拉伸应力进行校核计算,螺栓的有限元计算结果如图6 所示。
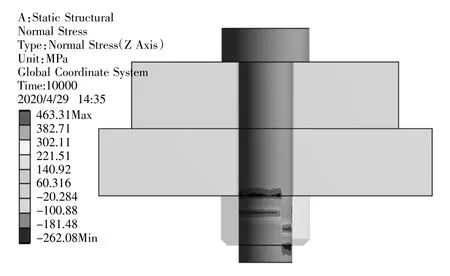
图6 螺栓连接结构的拉伸应力云图
2.6 理论计算与有限元计算结果对比
根据理论计算和有限元计算的结果汇总编制出螺栓拉应力表,见表格2。
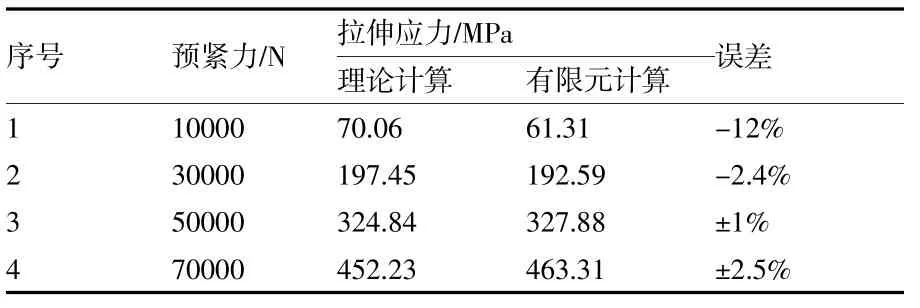
表2 拉伸应力对照表
根据理论计算与有限元计算结果对比可以看出,通过有限元计算的螺栓拉伸应力的误差范围较小,是可以接受的。
3 结论
本文采用Ansys Workbench 软件对螺栓连接进行有限元接触分析,并将计算结果与经典理论公式计算结果进行对比,为螺栓的设计计算提供了一种新的技术手段,同时为螺栓在工程中的实际应用提供一定的参考依据。
