应用零点定理和中值定理证明方程根的存在性的对比与分析

（洛阳师范学院数学科学学院 河南·洛阳 471934）

方程根的存在性在高等数学教学以及考研中都是一个非常重要的内容，具有极其重要的地位，也是一个比较困难的问题。零点定理和中值定理均可以证明方程根的存在性，在证明的过程中通常需要构造辅助函数,而在教学和辅导学生考研时发现这方面对于大多数学生来说是一个非常薄弱的环节.本文通过对考研中的试题和典型例题进行探究，对比分析得到证明的简便方法，从分析的过程中也可以看到如何寻找合适的辅助函数来证明所需要的结论。

首先给出几个定理。

从定理的内容可以看出，零点定理和中值定理都可以用来证明方程根的存在性或等式，那么在具体的应用中如何快速找到合适的定理需要我们进一步来探讨。从结论上来看，中值定理中有函数在两点处的值，对存在的来说，零点定理中是函数本身，而中值定理中都包含函数的导数，罗尔中值定理和拉格朗日中值定理只有一个函数，而柯西中值定理包含两个函数，在解题中我们可以抓住这个特点来判断用哪一个定理比较合适，从而更好的解决问题.另外在解题过程中一般来说所要证明的结论并不是标准的形式，因此需要构造辅助函数.那么如何构造合适的辅助函数，从而把原问题进一步转化为定理中的形式，这在数学中是一个重点和难点的内容.下面通过对考研中的试题和典型例题的分析及证明过程来探讨辅助函数的构造方法以及定理的应用条件.

分析：该例题是2020年考研数学二中的试题。（1）中要证明的表达式中对存在的来说，是函数本身，因此可考虑用零点定理来证明，由于题中不是标准的的形式，需改写为，因此要构造辅助函数，证明在内有根即可，另一方面注意到，因此可改写为，若令，只需证，因此也可考虑用罗尔中值定理来证明；（2）中要证明的结论中显然有函数值，由可知，对需要证明中的存在的来说，是函数的导数形式出现的，而且还含有的形式，即含有两个函数，因此可考虑用柯西中值定理来证明.

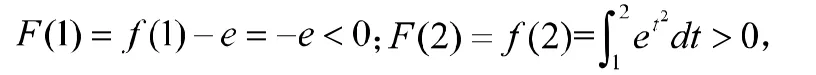
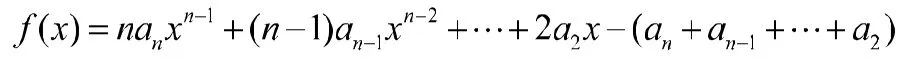
证明：令

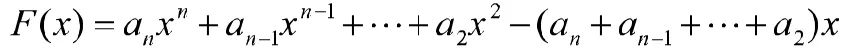
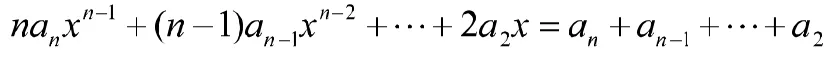
通过以上例题以及分析可知，在证明方程根的存在性时，要根据需要证明的结论来分析应用哪一个定理合适，并由证明等式的变形来构造合适的辅助函数.特别的在应用中值定理时，关键要把等式中的表达式写成导数的形式，这就要求我们对函数的导数或原函数要熟练掌握，灵活运用.另外例1中的（1）和例4均可以用零点定理和中值定理来证明，从分析和证明过程来看，用零点定理更直观、简便一些。