海港候潮锚地锚位数计算

连石水， 卢永昌， 孙继斌， 乔光全

(中交第四航务工程勘察设计院有限公司， 广东 广州510230)

1 候潮锚地锚位数的研究现状

港口经过十多年高速发展， 岸线资源变得越来越紧张， 大量码头需要通过开挖航道和港池建港。 为减少水域疏浚， 降低对环境的负面影响，压减工程投资， 船舶通航密度较小或大吨位的码头一般选择乘潮进出港， 并相应配置候潮锚地，确保船舶进出港安全。

在走访海事、 港口管理及使用单位和收集资料的基础上， 总结得出以下关于锚位数的确定方法:

1)海事、 港口管理及使用单位普遍认为锚位数与泊位数比例至少为1∶2， 当大风天气时最佳比例为1∶1。 此方法仅适用于避风锚地的锚位数计算[1]。

2)《海港总体设计规范》[2]和《海港工程设计手册》[3]均提出锚位数可根据反映船舶到港规律的排队论模型进行计算， 公式是基于船舶到港时间和装卸作业时间服从一定数学分布规律推算得到，并与泊位数有密切关系， 适用于待泊锚地的锚位数计算。

3)《海港工程设计手册》还提出“连续恶劣天数法” 和仿真分析方法， 前者过于笼统， 用于避风情况下锚位数计算， 没有体现台风预报的影响，且考虑船舶到港是均匀的， 结果偏大； 仿真分析方法可用于候潮锚地锚位数计算， 但过于繁琐。

2 候潮锚地锚位数计算方法

2.1 影响候潮锚地锚位数因素分析

通常情况下， 设置候潮锚地的码头靠船频率较低， 来船密度小， 一般不存在需要等待泊位的情况。 因此， 可忽略船舶在港装卸时间和泊位数的影响， 主要考虑船舶到港规律和潮汐特征影响。

通过调查了解， 允许夜间通航时， 只要潮位合适即可进出港， 但有些海域或部分货船夜间不允许进出港， 需要做更长时间等待， 为此还应考虑港口管理的有关要求。

综上， 候潮锚地锚位数应综合考虑船舶到潮汐特征、 航道乘潮保证率、 航道管理、 乘潮船舶数量及船舶到港时间规律等因素， 候潮锚地锚位数Mω1及在港乘潮船舶的保证率Qω1为:

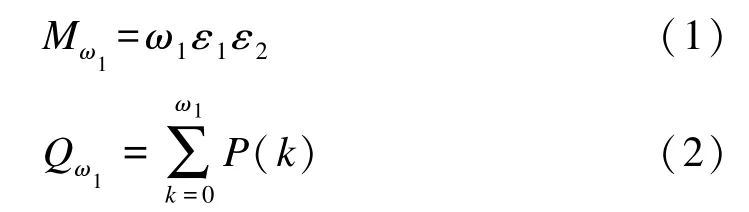
式中: ω1为保证率90%～99%时对应在港乘潮船舶数量； ε1为潮汐特征影响系数； ε2为航道管理影响系数；Qω1为在港有ω1艘乘潮船舶的保证率，即到港少于和等于ω1艘乘潮船舶的概率之和， 参照待泊锚地锚位数计算时保证率， 取90%～99%；P(k)为在港有k艘乘潮船舶的状态概率。

2.2 船舶到港规律及在港船舶状态概率

《海港工程设计手册》提出， 根据国内外大量的资料证实， 我国大连港(1979 年)、 秦皇岛港煤船(1980 年)、 秦皇岛港散粮船(I982—1984 年)、青岛港(1982 年)、 上海港散粮船(1982—1983 年)、黄埔港件杂货泊位(1981 年)、 天津港(2011 年)的船舶到达均服从泊松分布。

《海港总体设计规范》也认为船舶到港符合泊松分布规律。

张怀慧等[4]推导得出， 船舶到港规律服从二项分布， 其数学物理意义明确， 符合船舶到港分布的“客观规律”。 假定λ 为平均每天到达的乘潮船舶数量、n为t时间内到港船舶总数， 当n＞10、λ∕n≤0.1 时， 泊松分布是二项分布的一种近似，事实上， 到港船舶数量远大于10 艘， 通常情况下， 到港船舶服从泊松分布。 考虑到计算便捷，通常采用泊松分布计算， 其结果足够精确。

鲁凡[5]通过案例分析得到， 船舶到港时间间隔服从负指数分布假设， 即每天到港船舶数量服从泊松分析， 并且拟合得非常好。

刘敬贤等[6]根据天津港船舶交管中心(VTS 中心)提供的2003-01-01—2005-12-30 进出主航道船舶的记录资料(进出天津港主航道船舶数量统计分析均以天为统计最小时间单位)， 统计每天到(出)港船舶数量作为分析船舶进出主航道、进出港口概率分布的样本， 在统计过程中， 分进港和出港两个方面进行统计。 可以用正态分布密度函数曲线、泊松分布密度函数曲线来拟合统计， 其拟合程度较为理想。 通过卡方检验法， 正态分布的拟合程度优于泊松分布的拟合程度。

为简化计算， 将需要乘潮进出港船舶到港规律近似认为与港口所有船舶到港规律一致， 服从泊松分布， 则在港有k艘乘潮船舶的状态概率:

式中: λ 为平均每天到达的乘潮船舶数量。

2.3 潮汐特征影响系数

船舶通航窗口期和等待时间见图1， 对于任意时刻Ti在特定水位H=HN条件下， 计算每个潮周期和每个自然日的船舶通航窗口期和船舶需要等候潮位的时间(假设船舶需要的航行时间为N小时)。

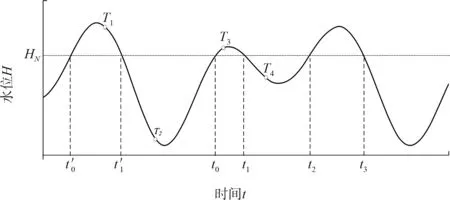
图1 船舶通航窗口期和等待时间

1) 通航窗口期: 计算每个潮周期内H＞HN的连续时间。 对于一日内的通航窗口期， 按照自然日取H＞HN的连续时间作为当日的通航窗口期， 对于单日内有多个高潮的自然日， 取连续时间长的作为当日的通航窗口期。

2)船舶等候时间的计算可以分为两种情况:

①Ti(i=1，2，…)时刻水位低于HN， 则候潮时间为第1 次高于HN且潮位窗口期大于N小时的水位对应的时刻与当前时刻的差值。 如图1 中T2时刻， 若t1-t0≥N， 则候潮时间为t0-T2， 若t1-t0＜N且t3-t2≥N， 则候潮时间为t2-T2。

②Ti(i=1，2，…)时刻水位高于HN， 如果第1次低于HN的时刻在N小时之后， 则等候时间为0；否则候潮时间为第1 次高于HN且潮位窗口期大于N小时的水位对应的时刻与当前时刻的差值。如图1 中T1时刻， 若-T1≥N， 则候潮时间为0，否则为时刻的等待时间与-T1之和， 其中时刻的等待时间可采用情况①计算。 特殊的，在通航窗口期小于N的时间段内的所有时间点的等待时间均按情况①计算， 如图1 中T3时刻， 若t1-t0＜N， 则计算方法和T2时刻相同。

考虑到乘潮船舶通常吨级较大， 且来船密度较小， 可根据逐时潮汐数据统计分析得到保证率达到90%的连续不能乘潮进出港时间t， 则ε1=t∕24，当t≤24 h时ε1取1.0。

2.3.1 案例1

大亚湾站2018 年潮位历时过程数据， 统计得到潮位历时曲线见图2。

图2 大亚湾站2018 年潮位历时曲线

经分析得到， 连续不能通航时间及频率见表1， 连续不能通航时间累积频率曲线见图3。

表1 连续不能通航时间及频率

续表1

图3 连续不能通航时间累积频率曲线

如图3 所示， 保证率达到90%对应连续不能乘潮进出港时间约为10 h， 则ε1=0.42(＜1)，取1。

2.3.2 案例2

钦州龙门站2018 年潮位历时过程数据， 统计得到潮位历时曲线见图4。

图4 钦州龙门2018 年潮位历时曲线

经分析得到， 乘潮历时为3 h， 保证率分别为50%、 70%、 80%和90%时连续不能通航时间累积频率曲线， 见图5。

图5 连续不能通航时间累积频率曲线

统计得到， 全国沿海港口航道乘潮保证率均不小于70%， 在乘潮保证率为70%、 80%和90%时对应保证率为90%连续不能通航时间分别为35、18 和14 h， 则ε1分别为1.46、 1 和1。

2.4 航道管理影响系数

通过调查了解， 允许夜间通航时， 只要潮位合适即可进出港， 但有些海域或部分货船夜间是不允许出港的， 需要做更长时间等待， 因此， 允许夜间通航时ε2取1； 禁止夜间通航， 一般不能进出港时间为12 h， 此时， ε2=1+12∕t， 当t≤24 h时ε2取1.5。

3 案例分析

以某港区30 万吨级航道为案例， 航道基本情况为:

1)通航标准: 按满足30 万吨级油船不满载(吃水19.6 m 控制)乘潮单向通航的标准建设， 通航宽度350 m(口门段加宽至384 m)， 设计底高程-20.6 m；2)乘潮水位: 乘潮历时3 h、 保证率90%，水位1.80 m； 3)潮汐特征: 海区为不正规半日潮；4)航道管理: 允许夜间通航； 5)30 万吨级油码头任务吞吐量为1 600 万t∕a， 乘潮船舶为25 万～30 万吨级油船， 预计有28 艘∕a， 航道可通航天数为321 d。

根据式(2)和(3)， 计算得到在港有ω1艘乘潮船舶的保证率Qω1， 见表2。

表2 在港有ω1 艘乘潮船舶的保证率Qω1

若取Qω1=0.95， 则ω1=1。 根据逐时潮汐数据统计分析得到保证率达到90%对应连续不能乘潮进出港时间为22 h， 则ε1=1； 航道允许夜间通航， 则ε2=1； 因此， 该港区30 万吨级油品码头所需候潮锚地锚位数Mω1=1。

4 结论

1)候潮锚地锚位数应综合考虑船舶到港时间规律、 潮汐特征、 航道管理等因素。

2)为简化计算， 将需要乘潮进出港船舶到港规律近似认为与港口所有船舶到港规律一致， 服从泊松分布。

3)在港有ω1艘乘潮船舶的保证率Qω1=P(k)，参照待泊锚地锚位数计算时保证率， 取90% ～99%， 据此求出在港乘潮船舶的数量ω1。

4)候潮锚地锚位数Mω1=ω1ε1ε2， 其中ε1为潮汐特征影响系数， 可根据逐时潮汐数据统计分析得到保证率达到90%对应连续不能乘潮进出港时间， 则ε1=t∕24， 当t≤24 h 时ε1取1.0； ε2为航道管理影响系数， 允许夜间通航时ε2取1； 禁止夜间通航， ε2=1+12∕t， 当t≤24 h 时ε2取1.5。