船舶进出船厢下沉量预测
2020-11-27傅陆志丹胡亚安
傅陆志丹, 胡亚安
(南京水利科学研究院, 通航建筑物建设技术交通行业重点实验室, 江苏 南京210029)
升船机作为耗水少、 运行速度快的通航建筑物对实现内河航运的通畅起着不可或缺的作用,我国至今已先后建成清江隔河岩、 清江高坝洲、红水河岩滩、 闽江水口、 乌江思林、 沙沱等钢丝绳卷扬垂直升船机, 长江三峡、 金沙江向家坝齿轮齿条爬升式升船机以及澜沧江景洪水力式升船机等多座大型升船机。 此外还有乌江构皮滩、 红水河龙滩和岩滩、 右江百色等多座垂直升船机正在设计建设中[1]。
升船机在空中运行阶段通常流程简单、 平稳顺畅。 而升船机船厢与上下游对接船舶进出船厢阶段, 由于承船厢一般采用厢形结构形式, 为了降低升船机的拖动功率并减少工程造价, 设计确定的船厢断面系数较小, 一般仅为2.0[2]。 由于承船厢尺寸限制, 船进出的运动过程中, 浅水效应和岸壁效应对船舶水动力有显著影响, 导致该阶段升船机运行流程较为复杂、 影响因素众多, 是升船机安全运行核心环节之一。 为准确判断船舶进出船厢的航行下沉量, 科学合理制定船舶吃水控制标准, 提高升船机安全运行和通过能力, 本文对船舶进出升船机船厢下沉量研究进行了总结,并提出今后的研究方向和内容。
1 船舶进出船厢航行特性
国际上普遍按照航道断面形式将航道分为3 类:非限制性航道、 挖槽式航道和限制性航道[3]。当船舶航行在无限深广的水域, 如海洋、 深水湖泊、 高水头枢纽工程的库区航道等, 断面系数趋于无穷大, 船舶航行过程中不存在阻塞效应, 船身周围的回流现象较限制性航道要小得多, 船体下沉也远小于限制性航道。
当船舶在挖槽式航道中航行时, 如一般内河航道、 进港港区航道、 浅海航道等, 断面系数主要受水深、 吃水比影响, 浅水效应对船舶航行产生诸多影响[4], 船体下沉及纵倾加剧。
限制性航道定义是因水面狭窄、 断面系数小而对船舶航行有明显限制作用的航道, 如运河、 渠道和河网地区的部分航道等。 与在非限制性航道航行有所不同, 流经船体的水流由于在空间上受到限制, 流态由在无限水域中的三维空间流动变为船体两侧的二维平面流动, 从而导致船体周围水压力的分布发生改变, 船舶阻力增加, 船体表面的水动力的大小和分布发生变化。 为了使船体受到的重力与浮力重新达到平衡, 船体就要在水中发生垂直方向上的移动, 这就是船舶的下沉[5], 见图1。

图1 船舶下沉现象概化
船舶进出船厢的过程可以看成是船舶在既窄又浅的特殊限制性航道中行驶[6-7], 见图2。 从外部水域条件分析, 相比进港航道和运河, 升船机船厢水域限制性更强、 水域有效过水断面更小,断面系数在1.6~2.0, 这会增加船舶航行下沉量。而且由于船厢的半封闭性, 在船舶进入船厢的过程中, 船舶对船厢水体的扰动与推进作用将会在船厢内部形成推进波系, 该波系在推进到船厢顶端的时候会与顶端厢壁发生固-壁反射现象, 并在船厢连接引航道的限制性水域内形成反射叠加波,进而造成船舶运动(下沉、纵倾、偏艏)的复杂性。因此, 须对船舶进出船厢下沉量进行专门研究。

图2 船舶进出船厢示意
2 船舶进出船厢下沉量主要影响因素
经过前人的研究, 影响船体下沉量的主要因素得到初步归纳。 JTJ 211—1999 《海港总平面设计规范》在确定航行下沉量时, 考虑了船舶载质量和航速两个因素; 国际航运协会(PIANC)《进港航道设计导则》推荐的公式中除考虑船舶载质量和航速两个因素外, 还考虑了水深、 断面系数和断面形状以及船舶类型的影响; 美国陆军工程师团《深水航道水力设计》推荐的航行下沉量计算公式考虑了船舶载质量、 船舶航速、 船舶方形系数、 船舶吃水和航道水深; 南京水利科学院对船舶进出船厢过程中下沉量的影响因素进行研究分析后得出主要影响因素为: 船舶航行方向、 船舶航速、 船厢水深和断面系数, 其中断面系数为航道过水断面面积与船舶过水断面面积之比。
综上, 影响船舶进出船厢下沉量主要因素有:1)船舶尺度; 2)船舶吃水; 3)船舶航速; 4)船厢尺度; 5)船厢水深; 6)船舶方型系数。
3 下沉量计算方法
已有不少学者对船舶下沉量计算进行了相关研究[8-13], 主要研究方法包含了3 大块: 理论分析、 物理模型试验和数值模拟, 但以理论分析和模型试验居多, 通过长期的研究, 形成了一系列船舶下沉量预测公式。
3.1 国际航运协会的《进港航道设计导则》中推荐的3 种下沉量计算公式
3.1.1 Barrass 公式
1981 年, Barrass[14]分析了在开敞水域和限制性航道不同船型(0.5≤Cb≤0.9)船舶的航行下沉量模型试验结果, 给出了船首下沉量的计算公式,其计算结果为平均下沉量:
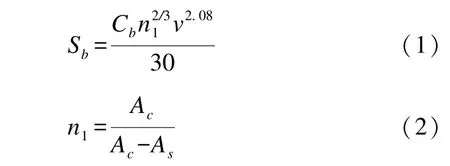
式中: Sb为船首下沉量; Cb为船舶方形系数;n1为断面系数; v 为船舶航速; Ac为航道过水断面面积; As为船舶过水断面面积。 南京水利科学研究院的研究表明, 船舶进出升船机船厢过程中,船尾发生的下沉量往往大于船首发生的下沉量,Barrass由于没有考虑纵倾变化, 计算数值偏大。
2009 年, Barrass 在《船舶航行下沉及相互影响》[15]一书中对船舶航行下沉量进行了系统的分析。 并对其1979 年提出的公式进行了修改。 新的公式适用于开敞水域和限制性航道, 其使用范围为: 1.1≤h∕T≤1.4, 4≤n≤10, 0.5≤Cb≤0.85,0≤v≤10.3 m∕s, 并不适用于升船机船厢中船舶下沉量的计算。

式中: S 为船舶下沉量; Cb为船舶方形系数; n 为断面系数, n=Ac∕As; v 为船舶航速; h 为航道水深; T 为船舶吃水。
3.1.2 Eryuzlu 公式
1978 年Eryuzlu 和Hausser[16]在横向无限水域和有限水深航道中进行了3 艘自行式超大型油轮(VLCC)模型试验, 发现了船舶下沉、 船速和吃水之间的关系, 得出了以其名字命名的经验公式, 和Barrass公式一样, Eryuzlu 给出的是船首下沉量的计算公式, 同时没有考虑阻塞效应对下沉量的影响。
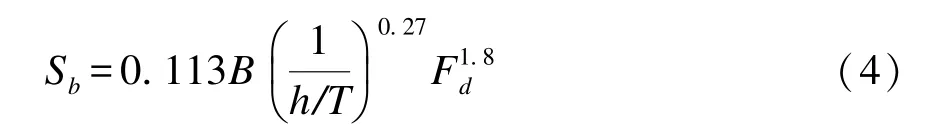
式中: Sb为船首下沉量; B 为船舶宽度; h 为航道水深; T 为船舶吃水; Fd为水深弗劳德数, Fd=
3.1.3 Huuska∕Guliev 公式
1976 年, Huuska[17]引入阻塞系数这一概念,并提出宽度受限水域中船舶下沉量估算公式, 其适用于无限水域航道、 限制性航道和运河, 但是不能应用于水深弗劳德数大于0.7 的情况, 且仅给出了船首最大下沉量的计算公式:
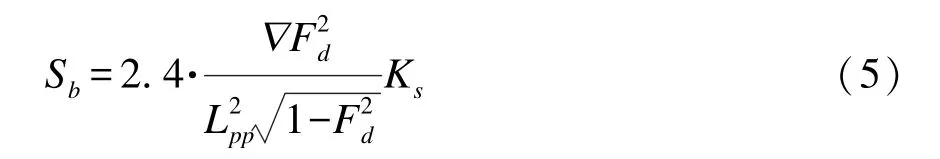
式中: Sb为船首下沉量; ∇为船舶排量; Fd为水深弗劳德数; Lpp为船舶两柱间长; 修正系数Ks取值如下:
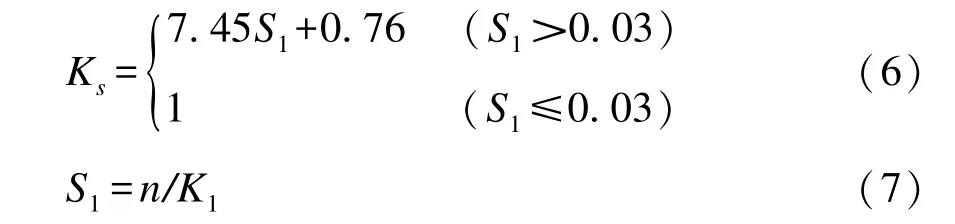
式中: K1为修正系数, 可通过图3 得出; n 为断面系数。 除此以外还有许多下沉量计算经验公式,主 要 包 括: Tuck 公 式[18]、 Romisch 公 式[19]、Millward 公式[20]、 Ankudinov 公式[21]、 ICORELS 公式[22]、 Yoshimura 公式、 Norrbin 公式[23]等, 这些公式都具有一定的适用范围和条件, 见表1。
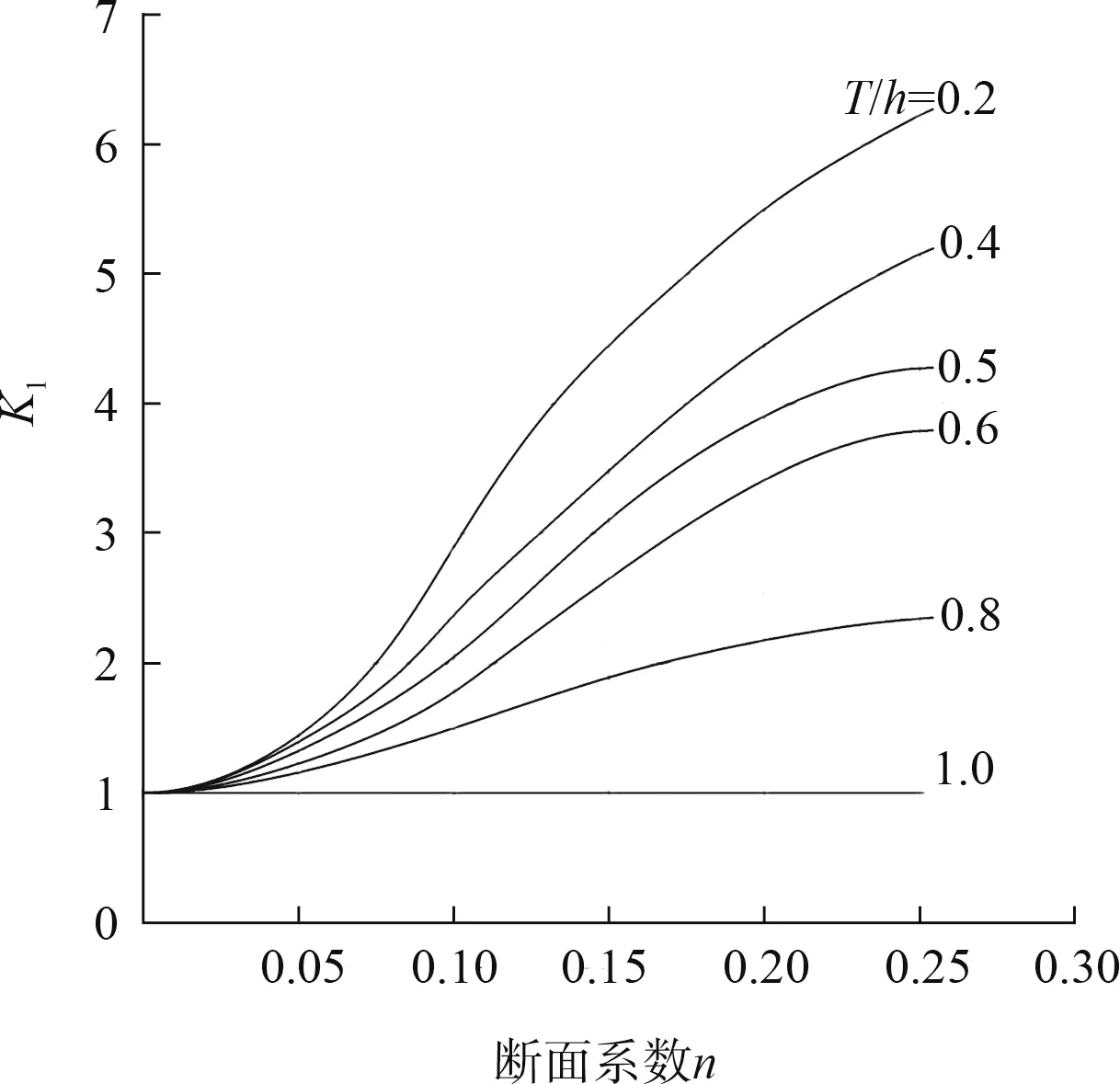
图3 修正系数K1
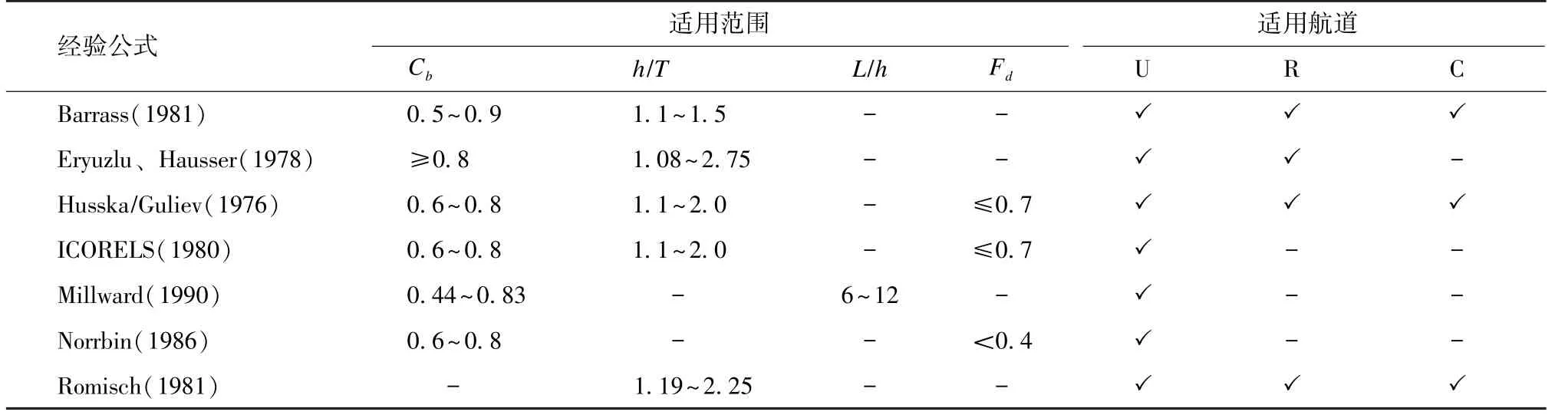
表1 常用经验公式使用条件
3.2 船舶进出升船机船厢下沉量计算方法
3.2.1 我国《升船机设计规范》公式
在GB 51177—2016 《升船机设计规范》条文说明中, 关于船舶进出厢下沉量推荐采用包纲鉴[24]于1991 年提出的经验公式, 该公式基于三峡、 陆水、大化等升船机的模型试验资料拟合得到:

式中: S 为下沉量; Fd为水深弗劳德数; n 为断面系数; T 为船舶吃水。
3.2.2 NHRI 下沉量经验公式
2011 年, 胡亚安等[25]为分析船舶下沉量的主要影响因素, 假定船舶在狭浅无限长区域航行,根据图1, 将坐标系固定在船舶上建立了以下方程组:
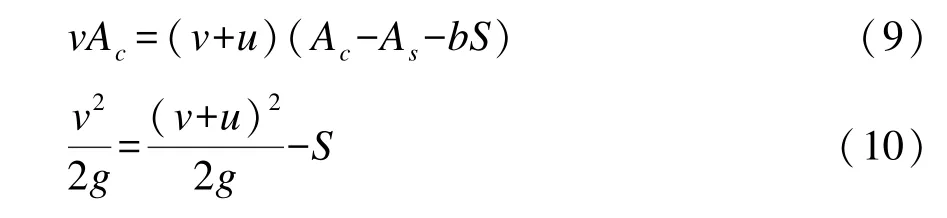
式中: v 为船舶航速; u 为船舶周围水流回流速度; Ac为航道过水断面面积; As为船舶过水断面面积; b 为航道宽度; S 为下沉量。
将三峡、 向家坝、 思林、 构皮滩[26]等升船机岀厢过程下沉量S、 船速v、 船厢水深h 和断面系数n 等变量通过无量纲处理后, 绘制的P-K 关系曲线见图4, 其中从图4 可以看出, 船舶航行下沉量与水深弗劳德数成二次函数关系, 由此提出了物理意义更为明确的NHRI 下沉量经验公式:

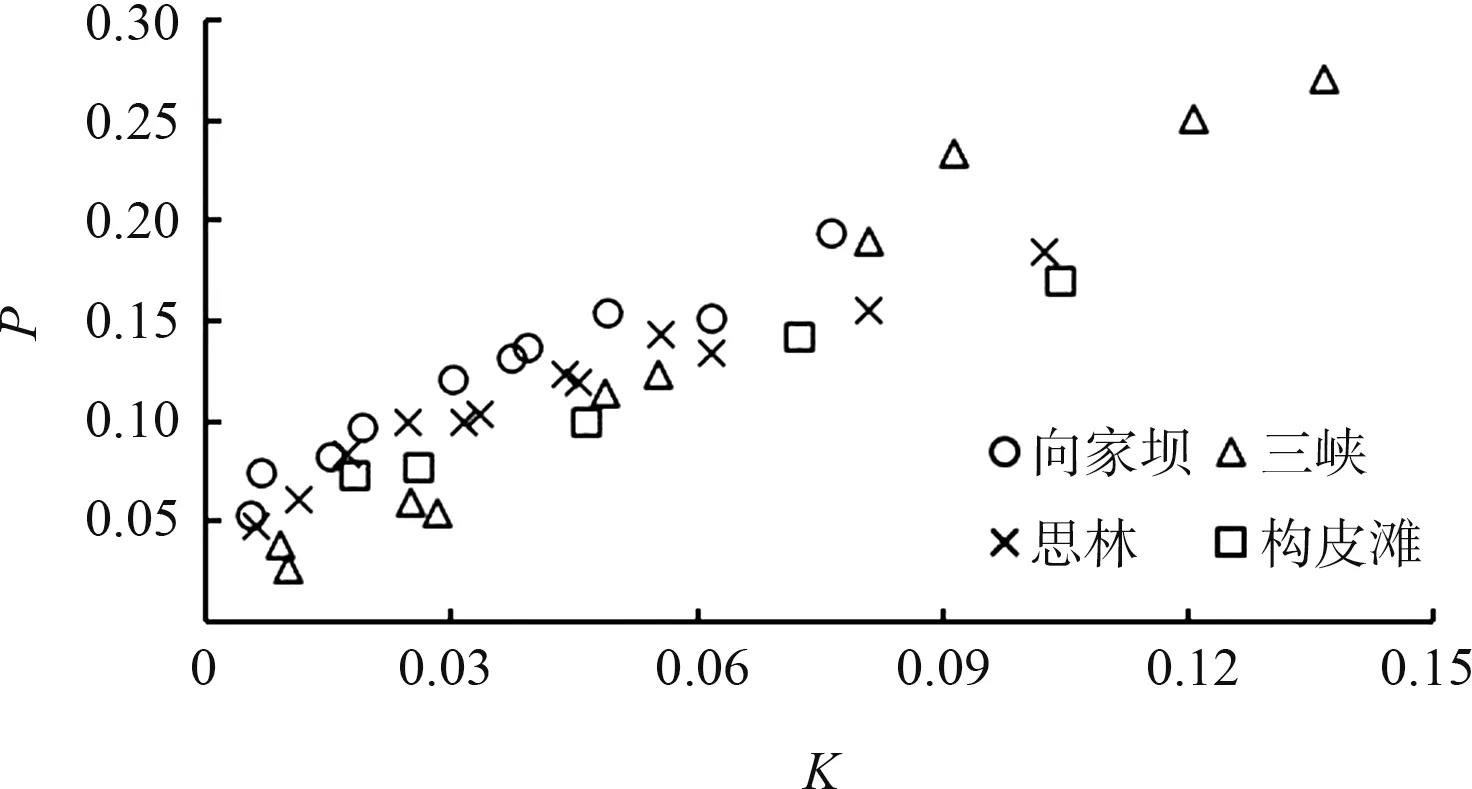
图4 不同升船机下沉量关系曲线
该公式的优点在于直接获取船舶下沉量, 经过最小二乘法拟合出的经验公式对符合试验条件的船舶下沉量预测精度高。 但是由于船模试验需要预先建造船模设置试验条件, 每进行一组试验耗资巨大且费时; 且每座升船机P-K 关系中斜率的取值没有得到规律性的总结, 限制了该公式的适用范围。
3.2.3 德国吕内堡升船机模型试验公式
2005 年, 德国联邦航道设计研究院针对现代大型内河船舶进出吕内堡升船机的问题开展了研究工作。 航行试验中发现船舶驶出升船机的速度受到阻塞系数的限制, 在航行试验中, 还对升船机上游侧非恒定流波动的水位进行了观测, 并对试验结果进行分析, 提出船舶出厢时最大航行下沉量的计算公式:
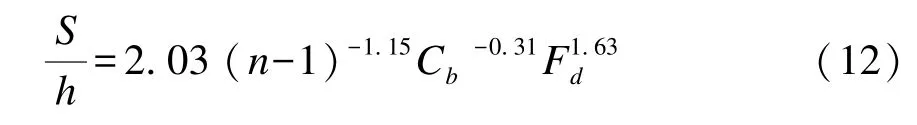
式中: S 为下沉量; h 为航道水深; n 为断面系数; Cb为船舶方形系数; Fd为水深弗洛德数。 该公式适应范围为: 1.17≤n≤3.26、 0.018≤Fd≤3.26、 0.83≤Cb≤0.96。
4 下沉量经验公式对比分析
以我国三峡升船机船舶出厢试验为例, 由于Barrass 公式断面系数适用范围在4 ~10, 故采用国际航运协会的《进港航道设计导则》中推荐的Eryuzlu 公式、 Huuska∕Guliev 公式以及我国《升船机设计规范》公式、 NHRI 公式和德国吕内堡升船机模型试验公式, 分析船舶航行下沉量计算结果, 与物理模型实测值对比结果见图5。 可以看出, 几种公式计算结果与实测值趋势一致, 其中Eryuzlu 公 式 计 算 结 果 偏 大, Huuska∕Guliev 公 式和我国《升船机设计规范》公式计算结果偏小,而NHRI 公式和德国吕内堡升船机模型试验公式与实测值吻合较好。 特别是当航速超过0.7m∕s,Eryuzlu 和Huuska∕Guliev 公式的计算结果与实测值误差更大。 因此, 当前国际航运协会推荐的3 种下沉量计算公式并不适用于我国升船机等通航建筑物的下沉量计算。

图5 不同计算方法计算船舶的航行下沉量对比
虽然NHRI 公式和德国吕内堡升船机模型试验公式与物理模型实测值吻合较好, 但在近期南京水利科学研究院船舶出厢下沉量影响因子试验研究[27]中发现, 在断面系数一样的情况下, 船厢过水断面存在不同组合的宽深比, 同一出厢航速下, 船舶下沉量也有一定差异, 见图6。 以上两个公式都没有考虑到这一情况,且欧洲船型与国内船型尺度有所不同, 针对我国升船机等通航建筑物, NHRI 公式还须进一步考虑船型对下沉量的影响。 同时, 当前研究均没有考虑船厢长度、 船舶在船厢中停泊位置以及船舶启动加速度对下沉量的影响, 这些因素也有待进行初步探讨。

图6 不同航速下船舶出厢断面系数与最大下沉量的关系
5 结语
1)与非限制性水域不同, 升船机船厢外部水域条件和船厢的半封闭性都会导致船舶运动的复杂性, 须对进出船厢船舶的下沉量进行专门研究,主要影响因素有: 船舶尺度、 船舶吃水、 船舶航速、 船厢尺度、 船厢水深和船舶方型系数。
2)目前国内外已有一系列的下沉量计算公式,但现有计算方法大多是针对船舶在无限水域或是进港航道、 运河中的船舶航行下沉量, 且有较为复杂和严格的约束条件。
3)对于升船机船厢这一特殊限制性航道, 虽然已有与实测值吻合较好的经验公式, 仍有相关问题有待进一步深化研究。 尚须对断面系数相同、船厢不同宽深组合对下沉量的影响进行研究, 同时在已有公式中, 补充船型对下沉量的影响。 有待研究船厢长度、 船舶在船厢中停泊位置以及船舶启动加速度等因素对下沉量的影响。
